Matrice simmetrica

In questa pagina troverai la spiegazione di cosa sono le matrici simmetriche. Inoltre, ti mostriamo come identificare rapidamente quando una matrice è simmetrica, insieme a diversi esempi per non avere dubbi. Troverai anche tutte le proprietà delle matrici simmetriche. E infine, spieghiamo una caratteristica particolare che possiede qualsiasi matrice quadrata: può essere scomposta nella somma di una matrice simmetrica e di una matrice antisimmetrica.

Cos’è una matrice simmetrica?

La definizione di matrice simmetrica è la seguente:

Una matrice simmetrica è una matrice quadrata la cui trasposta è uguale alla matrice stessa.

$A^t = A$

Oro

$A^t$

rappresenta la matrice trasposta di

$A$

Una volta conosciuto il concetto di matrice simmetrica, vedremo come qualsiasi matrice simmetrica possa essere facilmente identificata:

Quando una matrice è simmetrica?

Riconoscere la struttura di una matrice simmetrica è molto semplice: l’elemento di riga i e colonna j deve essere identico all’elemento di riga j e colonna i . E i valori della diagonale principale della matrice possono essere qualsiasi.

Esempi di matrici simmetriche

Ecco alcuni esempi di matrici simmetriche per aiutarti a capire:

Esempio di matrice simmetrica di ordine 2 × 2

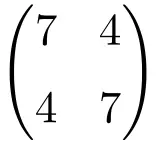
esempio di matrice simmetrica di dimensione 2x2

Esempio di matrice simmetrica di dimensione 3×3

esempio di matrice simmetrica di dimensione 3x3

Esempio di matrice simmetrica di dimensione 4×4

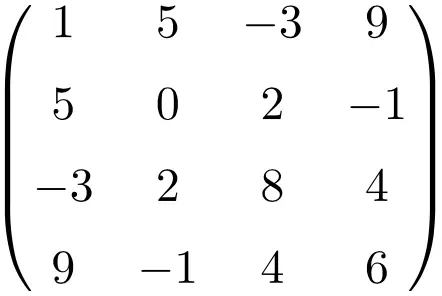
esempio di matrice simmetrica di dimensione 4x4

Trasponendo queste tre matrici verifichiamo che sono simmetriche, perché le matrici trasposte sono equivalenti alle rispettive matrici originali.

Perché si chiama matrice simmetrica?

Se osservi attentamente gli esempi precedenti, la diagonale principale di una matrice simmetrica è un asse di simmetria, o in altre parole, funge da specchio tra i numeri sopra la diagonale e quelli sotto. Per questo motivo questi tipi di matrici sono dette simmetriche.

Proprietà delle matrici simmetriche

Le caratteristiche delle matrici simmetriche sono le seguenti:

L’aggiunta (o la sottrazione) di due matrici simmetriche fornisce un’altra matrice simmetrica. Poiché trasporre due matrici aggiunte (o sottratte) equivale a trasporre ciascuna matrice separatamente:

$\displaystyle \left(A+B\right)^t = A^t+B^t = A+B$

Qualsiasi matrice simmetrica moltiplicata per uno scalare dà origine anche a un’altra matrice simmetrica.

Allo stesso modo, il prodotto matriciale tra due matrici simmetriche non è sempre uguale a un’altra matrice simmetrica, solo se e solo se le due matrici possono essere commutate. Questa condizione può essere dimostrata con la proprietà di moltiplicazione di matrici trasposte:

$\displaystyle \left(A\cdot B\right)^t = B^t\cdot A^t = BA=AB$

La potenza di una matrice simmetrica dà origine a un’altra matrice simmetrica, purché l’esponente sia un numero intero.

Ovviamente la matrice unitaria e la matrice zero sono esempi di matrici simmetriche.

Una matrice congruente a una matrice simmetrica deve essere anche simmetrica.

Se una matrice simmetrica è regolare o invertibile, anche la sua matrice inversa è simmetrica.

Lo stesso vale per l’aggiunta di una matrice simmetrica: la matrice aggiunta di una matrice simmetrica fornisce come soluzione un’altra matrice simmetrica.

Una vera matrice simmetrica è anche una matrice normale.

Poiché le matrici simmetriche sono un caso speciale di matrici hermitiane, tutti gli autovalori (o autovalori) di una matrice simmetrica sono numeri reali.

Il teorema spettrale ci dice che tutte le matrici i cui elementi sono reali sono matrici diagonalizzabili e, inoltre, la diagonalizzazione viene effettuata mediante una matrice ortogonale. Pertanto, tutte le matrici reali simmetriche sono diagonalizzate ortogonalmente.

D’altra parte, le matrici simmetriche con numeri complessi possono essere diagonalizzate tramite una matrice unitaria.

La matrice dell’Assia è sempre simmetrica.

Scomposizione di una matrice quadrata in una matrice simmetrica e una matrice antisimmetrica

Una caratteristica speciale delle matrici quadrate è che possono essere scomposte nella somma di una matrice simmetrica più una matrice antisimmetrica.

La formula che ci permette di farlo è la seguente:

$\displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}$

Dove C è la matrice quadrata che vogliamo scomporre, C la ^sua trasposta, ed infine S e A sono rispettivamente le matrici simmetrica e antisimmetrica in cui viene scomposta la matrice C.

Di seguito hai un esercizio risolto per vedere come è fatto. Scomponiamo la seguente matrice:

$\displaystyle C=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

Calcoliamo la matrice simmetrica e antisimmetrica con le formule:

$\displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}$

$\displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}$

E possiamo verificare che l’equazione sia soddisfatta sommando le due matrici:

$\displaystyle C=S+A \quad ?$

$\displaystyle\begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}+\begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

$\displaystyle C=S+A$

✅