Matrici simili o simili

In questa pagina troverai la spiegazione delle matrici simili, chiamate anche matrici simili. Inoltre, ti mostriamo un chiaro esempio di due matrici simili e tutte le proprietà di questo tipo di matrici affinché tu non abbia dubbi. Infine, sarai anche in grado di vedere come si relazionano alle matrici congruenti.

Cosa sono le matrici simili (o simili)?

La definizione di matrici simili è la seguente:

due matrici

$A$

$B$

sono simili (o simili) se esiste una matrice

$P$

con cui è soddisfatta la seguente condizione:

$P^{-1}AP = B$

O equivalente:

$AP = PB$

In effetti, la matrice

$P$

funge da matrice di cambiamento di base. Pertanto, ciò che significa questa equazione è che la matrice

$A$

può essere espresso in un’altra base (

$P$

), che dà origine alla matrice

$B$

Questo termine può anche essere chiamato trasformazione di somiglianza , poiché stiamo effettivamente trasformando la matrice

$A$

nella matrice

$B$

Ovviamente la matrice

$P$

deve essere una matrice regolare o non degenere (determinante diverso da zero).

Possiamo invece indicare che due matrici sono simili alla seguente espressione:

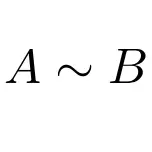
Questa classe di matrici è più importante di quanto sembri per l’algebra lineare. Vengono utilizzati principalmente per matrici diagonalizzabili, perché la procedura per diagonalizzare qualsiasi matrice si basa sul concetto di similarità di matrice.

Infatti, il processo di diagonalizzazione di una matrice comporta il calcolo di una matrice simile che, allo stesso tempo, è una matrice diagonale. Puoi vedere come si fa in come diagonalizzare una matrice .

Esempio di matrici simili o simili

Poi vedremo un esempio di matrici simili di dimensione 2×2 per finire di assimilare il concetto.

Le matrici quadrate A e B sono simili tra loro attraverso la matrice invertibile P:

$\displaystyle A= \begin{pmatrix}-1&2\\[1.1ex] 3&1\end{pmatrix} \qquad B= \begin{pmatrix}-5&-3\\[1.1ex] 6&5\end{pmatrix}$

$\displaystyle P= \begin{pmatrix}2&1\\[1.1ex] -1&0\end{pmatrix}$

Per dimostrare che si tratta di matrici tra loro simili, dobbiamo prima calcolare la matrice inversa di P:

$\displaystyle P^{-1}= \begin{pmatrix}0&-1\\[1.1ex] 1&2\end{pmatrix}$

E ora controlliamo che siano simili eseguendo il prodotto di matrici che definisce la somiglianza di due matrici:

$\displaystyle P^{-1}AP = B \quad ?$

$\displaystyle P^{-1}AP = B$

✅

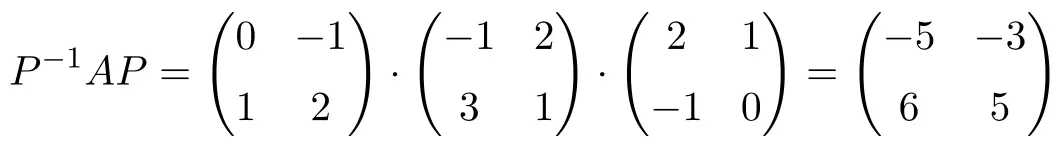
Sì, la relazione di similarità è soddisfatta, quindi sono matrici simili.

Proprietà simili della matrice

Due matrici simili A e B condividono le seguenti caratteristiche:

Stesso grado.

$rg(A)=rg(B)$

Le determinanti delle due matrici sono le stesse.

$det(A)=det(B)$

Stessa tracciatura.

$tr(A)=tr(B)$

Stessi autovalori (o autovalori). Tuttavia, gli autovettori (o autovettori) sono generalmente diversi.

Stesso polinomio caratteristico e polinomio minimo.

La trasposizione di una matrice è simile alla matrice originale.

La matrice B può essere trovata applicando operazioni elementari sulle righe della matrice A, e viceversa.

Ovviamente la somiglianza si riflette. Cioè, se A è simile a B, allora anche B è simile ad A.

Inoltre, anche la somiglianza delle matrici è simmetrica. In altre parole, se con la matrice P si può ottenere la matrice simile ad A (B), con la stessa matrice P si può ottenere anche la matrice simile a B (A):

$B=P^{-1}AP$

$A=PBP^{-1}$

Inoltre la somiglianza è transitiva. Quindi se la matrice A è simile alla matrice B e la matrice B è simile alla matrice C, anche la matrice A è simile alla matrice C.

$\left. \begin{array}{l}A\sim B \\[2ex] B \sim C \end{array}\right\} \longrightarrow A \sim C$

Infine, ogni matrice è simile ad una matrice a dente di sega. E da questa proprietà si può dedurre il seguente corollario: ogni matrice quadrata è simile ad una matrice triangolare.

matrici congruenti

D’altra parte, esiste anche un’altra relazione molto simile tra le matrici ma invece di essere con la matrice inversa, è con la matrice trasposta. Questa si chiama congruenza .

Due matrici A e B sono congruenti se esiste una matrice invertibile P con la quale è soddisfatta la seguente uguaglianza:

$P^tAP = B$

Come puoi vedere, questo è l’analogo di matrici simili ma con la matrice trasposta.

Cosa sono le matrici simili (o simili)?

Esempio di matrici simili o simili

Proprietà simili della matrice

matrici congruenti

Lascia un commento Annulla risposta