Matrice antisimmetrica

In questa pagina spieghiamo cosa sono le matrici antisimmetriche. Inoltre, potrai vedere diversi esempi e la sua struttura tipica per capirlo perfettamente. Spieghiamo anche la particolarità del calcolo del determinante di una matrice antisimmetrica e tutte le proprietà di questo tipo di matrice. E infine, scoprirai come scomporre qualsiasi matrice quadrata nella somma di una matrice simmetrica più un’altra matrice antisimmetrica.

Cos’è una matrice antisimmetrica?

La definizione di matrice antisimmetrica è la seguente:

Una matrice antisimmetrica è una matrice quadrata la cui trasposta è uguale al negativo della matrice.

$A^t = -A$

Oro

$A^t$

rappresenta la matrice trasposta di

$A$

$-A$

è la matrice

$A$

con tutti i suoi elementi cambiò segno.

Esempi di matrici antisimmetriche

Una volta conosciuto il concetto di matrice antisimmetrica, vedremo diversi esempi di matrici antisimmetriche per comprenderlo meglio:

Esempio di matrice antisimmetrica di ordine 2 × 2

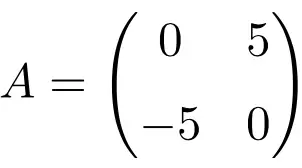
esempio di matrice antisimmetrica di dimensione 2x2

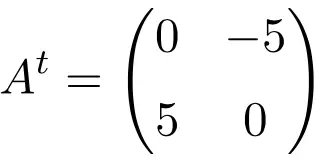
esercizio risolto di matrice antisimmetrica di dimensione 2x2

Esempio di matrice antisimmetrica di dimensione 3×3

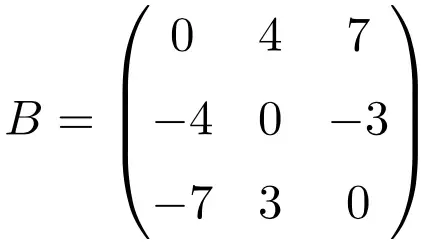
esempio di matrice antisimmetrica di dimensione 3x3

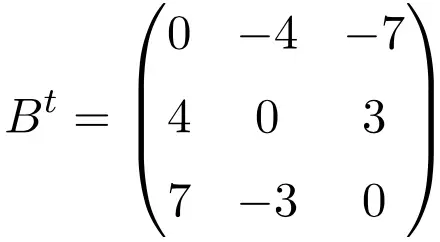
esercizio risolto di matrice antisimmetrica di dimensione 3x3

Esempio di matrice antisimmetrica di dimensione 4×4

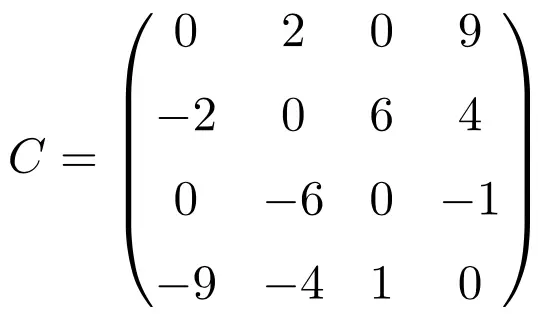
esempio di matrice antisimmetrica di dimensione 4x4

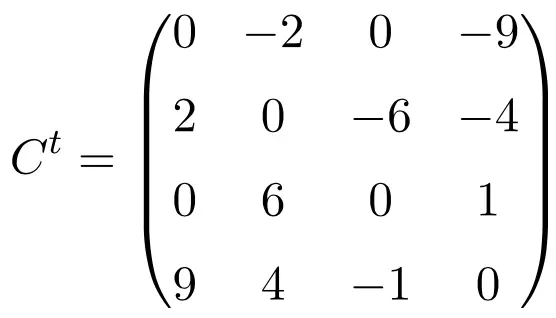
esercizio risolto di matrice antisimmetrica di dimensione 4x4

Trasponendo queste tre matrici verifichiamo che sono antisimmetriche, perché le matrici trasposte sono equivalenti alle rispettive matrici originali cambiate segno.

Struttura di una matrice antisimmetrica

Affinché la condizione di matrice antisimmetrica sia soddisfatta, devono avere sempre lo stesso tipo di struttura: i numeri sulla diagonale principale sono tutti uguali a zero e l’elemento della riga i e della colonna j è il negativo dell’elemento della riga j e della colonna io . In altre parole, la forma delle matrici antisimmetriche è la seguente:

$\displaystyle \begin{pmatrix} 0 & a & b & \cdots & c\\[1.1ex]-a & 0 & d & \cdots &e\\[1.1ex]-b & -d & 0 & \cdots & f\\[1.1ex]\vdots & \vdots & \vdots & \ddots & \vdots\\[1.1ex] -c & -e & -f & \cdots & 0\end{pmatrix}$

Pertanto, la diagonale principale di una matrice antisimmetrica funge da asse di antisimmetria. Da qui deriva il nome di questa particolare matrice.

Determinante di una matrice antisimmetrica

Il determinante di una matrice antisimmetrica dipende dalla dimensione di detta matrice. Ciò è dovuto alle proprietà dei determinanti:

$\displaystyle \text{det}(A)=\text{det}(A^t)=\text{det}(-A)=(-1)^n \text{det}(A)$

Pertanto, se la matrice antisimmetrica è di ordine dispari, il suo determinante sarà pari a 0 . Se invece la matrice antisimmetrica è di dimensione pari, il determinante può assumere qualsiasi valore.

Pertanto, una matrice antisimmetrica di dimensione dispari è una matrice singolare o degenere. D’altra parte, una matrice antisimmetrica di ordine pari è una matrice regolare.

Proprietà delle matrici antisimmetriche

Le caratteristiche delle matrici antisimmetriche sono le seguenti:

Aggiungendo (o sottraendo) due matrici antisimmetriche si ottiene un’altra matrice antisimmetrica. Poiché trasporre due matrici aggiunte (o sottratte) equivale a trasporre ciascuna matrice separatamente:

$\displaystyle \left(A+B\right)^t = A^t+B^t = -A-B$

Qualsiasi matrice antisimmetrica moltiplicata per uno scalare dà origine anche a un’altra matrice antisimmetrica.

La potenza di una matrice antisimmetrica è equivalente a una matrice antisimmetrica o a una matrice simmetrica. Se l’esponente è un numero pari, il risultato della potenza è una matrice simmetrica, ma se l’esponente è un numero dispari, il risultato della potenza è una matrice antisimmetrica. Puoi consultare in questo link cos’è una matrice simmetrica .

La traccia di una matrice antisimmetrica è sempre uguale a zero.

La somma di una qualsiasi matrice antisimmetrica più la matrice unitaria dà origine a una matrice invertibile.

$\displaystyle \text{det}(A+I)\neq 0$

Tutti gli autovalori reali (o autovalori) di una matrice antisimmetrica sono 0. Tuttavia, una matrice antisimmetrica può anche avere autovalori complessi.

Tutte le matrici antisimmetriche sono matrici normali. Pertanto sono soggetti al teorema spettrale, secondo il quale una matrice antisimmetrica può essere diagonalizzata da una matrice unitaria.

Scomposizione di una matrice quadrata in una matrice simmetrica e una matrice antisimmetrica

Una caratteristica speciale delle matrici quadrate è che possono essere scomposte nella somma di una matrice simmetrica più una matrice antisimmetrica.

La formula che ci permette di farlo è la seguente:

$\displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}$

Dove C è la matrice quadrata che vogliamo scomporre, C la ^sua trasposta, ed infine S e A sono rispettivamente le matrici simmetrica e antisimmetrica in cui viene scomposta la matrice C.

Di seguito hai un esercizio risolto per dimostrare la formula. Scomponiamo la seguente matrice:

$\displaystyle C=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}$

Calcoliamo la matrice simmetrica e antisimmetrica con le formule:

$\displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}$

$\displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}$

E possiamo verificare che l’equazione sia soddisfatta sommando le due matrici:

$\displaystyle C=S+A \quad ?$

$\displaystyle\begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}+\begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}$

$\displaystyle C=S+A$

✅