▷ Teorema del resto: cos'è, esempi ed esercizi risolti ✅

Qui troverai la spiegazione di cos’è il teorema dei resti (o teorema dei resti) e come si applica ai polinomi. Potrai anche vedere esempi e, inoltre, esercitarti con esercizi risolti passo passo sul teorema del resto.

Qual è il teorema del resto?

In matematica, il teorema del resto dice che il resto della divisione di qualsiasi polinomio P(x) per un altro polinomio della forma (xa) è uguale al valore numerico del polinomio P(x) per il valore x=a, In in altre parole, il resto della divisione P(x):(xa) è equivalente a P(a).

Esempio del teorema del resto

Una volta visto cos’è il teorema del resto, vediamo un esempio pratico della sua applicazione:

Calcola il resto della divisione tra i due polinomi seguenti:

$P(x) = x^3+2x^2-4x+3 \qquad \qquad Q(x)=x-1$

$\cfrac{P(x)}{Q(x)}$

Per trovare il resto (o residuo) della divisione polinomiale possiamo avvalerci del teorema dei resti, perché in questo caso il polinomio divisore è della forma (xa), cioè è di primo grado, il coefficiente di la variabile x è 1 e ha un termine indipendente.

Applichiamo quindi il teorema del resto, che dice che il resto di una divisione come questa è uguale al valore numerico del polinomio del dividendo valutato nel termine indipendente del polinomio del divisore cambiato di segno, cioè P (1).

Pertanto, per trovare il resto della divisione, dobbiamo valutare il polinomio in x=1:

$\begin{aligned} P(1) &= 1^3+2\cdot 1^2-4\cdot 1+3\\[2ex] &= 1+2\cdot 1-4 \cdot 1+3 \\[2ex] & = 1+2-4+3 \\[2ex] & =\bm{2} \end{aligned}$

Il resto della divisione tra i polinomi è quindi 2 .

D’altra parte possiamo anche verificare con la regola di Ruffini per la divisione dei polinomi che il resto coincide con il risultato che abbiamo trovato:

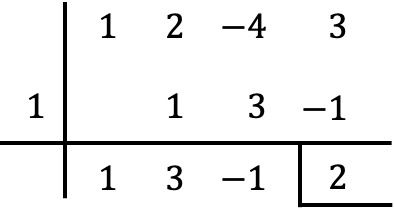
Come puoi vedere, è molto più veloce e più facile determinare il resto di una divisione di un polinomio per un binomio con il teorema dei resti che con la regola di Ruffini, perché vengono eseguiti molti meno calcoli.

Teorema del resto e dei fattori

Dal teorema del resto e dalla definizione della radice (o zero) di un polinomio si deduce il teorema dei fattori. Quindi il teorema dei fattori implica quanto segue:

Il teorema dei fattori dice che un polinomio P(x) è divisibile per un altro polinomio della forma (xa) se, e solo se, P(a)=0. E, in questo caso, ciò significa che a è una radice o uno zero del polinomio P(x).

Inoltre, secondo il teorema del resto, ciò significa che se un polinomio è divisibile per un altro polinomio, il resto di detta divisione è zero, poiché P(a)=0.

Ad esempio, se abbiamo un certo polinomio:

$P(x)=x^2+2x-8$

Questo polinomio è divisibile per il binomio (x-2) perché P(2)=0:

$\begin{aligned} P(2) &= 2^2+2\cdot 2-8\\[2ex] &= 4+4-8 \\[2ex] & =\bm{0} \end{aligned}$

Poiché x=2 annulla il polinomio P(x), ciò significa che x=2 è radice di detto polinomio.

E inoltre, poiché P(2)=0, grazie al teorema del resto possiamo sapere che il resto della divisione

$\cfrac{x^2+2x-8}{x-2}$

è uguale a 0.

Esercizi risolti del teorema del resto

Per completare la comprensione del teorema del resto, abbiamo preparato alcuni esercizi risolti passo dopo passo in modo che tu possa esercitarti. Ti consigliamo di provare prima l’esercizio e poi di verificare se lo hai eseguito correttamente.

Esercizio 1

Trovare, con il teorema del resto, il resto della divisione polinomiale

$\cfrac{P(x)}{Q(x)}$

, essendo i polinomi coinvolti nell’operazione:

$P(x) =x^3+4x^2-2x+1\qquad \qquad Q(x)=x-2$

Vedi la soluzione

Il polinomio divisore è composto solo da un termine di primo grado e da un termine indipendente e, inoltre, il coefficiente del termine di primo grado è 1. Possiamo quindi utilizzare il teorema del resto.

E per applicare il teorema del resto basta valutare il polinomio del dividendo nel termine indipendente del polinomio divisore cambiato segno, ovvero bisogna calcolare P(2).

$\begin{aligned} P(2) &= 2^3+4\cdot 2^2-2\cdot 2+1\\[2ex] &=8+4\cdot 4-2\cdot 2+1 \\[2ex] & = 8+16-4+1 \\[2ex] & =\bm{21} \end{aligned}$

Il resto della divisione tra i due polinomi è quindi 21 .

Esercizio 2

Dato il polinomio

$P(x)=x^4-2x^3+5x^2-3x+4 ,$

Trova il resto ottenuto dividendolo per ciascuno dei seguenti polinomi:

$\text{A)} \ \left(x-1 \right)$
$\text{B)} \ \left(x+1 \right)$
$\text{C)} \ \left(x+2 \right)$
$\text{D)} \ \left(x-3 \right)$

Vedi la soluzione

Poiché tutti i polinomi di divisione soddisfano le condizioni del teorema del resto, possiamo usare questo teorema per determinare il resto di ciascuna divisione:

$\begin{aligned} \mathbf{A}\bm{)} \ P(1) &= 1^4-2\cdot 1^3+5\cdot 1^2-3\cdot 1+4\\[2ex] &=1-2\cdot 1+5\cdot 1 -3 \cdot 1+4 \\[2ex] & = 1-2+5-3+4 \\[2ex] & =\bm{5} \end{aligned}$

$\begin{aligned} \mathbf{B}\bm{)} \ P(-1) &= (-1)^4-2\cdot (-1)^3+5\cdot (-1)^2-3\cdot (-1)+4\\[2ex] &=1-2\cdot (-1)+5\cdot 1 -3 \cdot (-1)+4 \\[2ex] & = 1+2+5+3+4 \\[2ex] & =\bm{15} \end{aligned}$

$\begin{aligned} \mathbf{C}\bm{)} \ P(-2) &= (-2)^4-2\cdot (-2)^3+5\cdot (-2)^2-3\cdot (-2)+4\\[2ex] &=16-2\cdot (-8)+5\cdot 4 -3 \cdot (-2)+4 \\[2ex] & = 16+16+20+6+4 \\[2ex] & =\bm{62} \end{aligned}$

$\begin{aligned} \mathbf{D}\bm{)} \ P(3) &= 3^4-2\cdot 3^3+5\cdot 3^2-3\cdot 3+4\\[2ex] &=81-2\cdot 27+5\cdot 9 -3 \cdot 3+4 \\[2ex] & = 81-54+45-9+4 \\[2ex] & =\bm{67} \end{aligned}$

Esercizio 3

Calcola quanto dovrebbe valere il parametro

$m$

in modo che il resto della divisione dei polinomi

$\cfrac{P(x)}{Q(x)}$

essere uguale a 3, essendo entrambi polinomi:

$P(x) =x^3-5x^2-mx+9 \qquad \qquad Q(x)=x+3$

Vedi la soluzione

In questo caso particolare il polinomio divisore è formato da un monomio di primo grado e da un termine indipendente e, inoltre, il coefficiente del monomio di primo grado è 1. Possiamo quindi utilizzare il teorema del resto.

E per usare il teorema del resto basta sostituire con un cambio di segno il termine indipendente del polinomio divisore dove nel polinomio diviso c’è una x, dobbiamo quindi risolvere P(-3).

$\begin{aligned} P(-3) &=(-3)^3-5\cdot (-3)^2-m\cdot (-3)+9\\[2ex] &=-27-5\cdot 9 -m\cdot (-3)+9 \\[2ex] & = -27-45+3m+9 \\[2ex] & =3m-63 \end{aligned}$

Ma ovviamente otteniamo un risultato basato sull’incognita

$m.$

Tuttavia, la formulazione del problema ci dice che il resto deve essere uguale a tre, quindi dobbiamo impostare il resto trovato uguale a 3:

$3m-63 = 3$

E infine risolviamo l’equazione:

$3m = 3+63$

$3m = 66$

$m = \cfrac{66}{3}$

$\bm{m = 22}$

Esercizio 4

Determinare con il teorema del fattore e del resto il polinomio

$P(x)$

è divisibile per il polinomio

$Q(x).$

$P(x) =-2x^3-5x^2-x+2 \qquad \qquad Q(x)=x+2$

Vedi la soluzione

Quindi il polinomio

$P(x)$

essere divisibile per il polinomio

$Q(x)$

la divisione tra questi due polinomi deve essere esatta e quindi il resto deve essere zero.

Quindi, poiché il polinomio divisore è

$(x+2),$

Dal teorema dei fattori e dal teorema del resto sappiamo che il polinomio

$P(x)$

sarà divisibile per il polinomio

$Q(x)$

se è pieno

$P(-2)=0.$

Dobbiamo quindi vedere se questa uguaglianza è verificata:

$P(-2)=0 \quad \color{blue} \bm{?}$

$\begin{aligned} P(-2) &=-2\cdot (-2)^3-5\cdot (-2)^2-(-2)+2\\[2ex] &=-2 \cdot (-8) -5 \cdot 4+2 +2\\[2ex] & =16-20+2+2 \\[2ex] & =0\end{aligned}$

Anzi, il resto della divisione

$\cfrac{P(x)}{Q(x)}$

è uguale a 0, quindi il polinomio

$P(x)$

Sì, è divisibile per l’altro polinomio

$Q(x).$

Cosa ne pensi della spiegazione? Ti è piaciuto? Speriamo! Non dimenticare che puoi lasciarci i tuoi suggerimenti o domande nei commenti. ⬇⬇⬇ Vi leggiamo tutti! 😁😁

Teorema del resto (o residuo).

Qual è il teorema del resto?

Esempio del teorema del resto

Teorema del resto e dei fattori

Esercizi risolti del teorema del resto

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Lascia un commento Annulla risposta