Regola di Cramer: Mathority

In questa pagina vedrai cos’è la regola di Cramer e, inoltre, troverai esempi ed esercizi con la risoluzione di sistemi di equazioni secondo la regola di Cramer.

Qual è la regola di Cramer?

La regola di Cramer è un metodo utilizzato per risolvere sistemi di equazioni mediante determinanti. Vediamo come si usa:

Consideriamo un sistema di equazioni:

$\begin{cases} ax+by+cz= \color{red}\bm{j} \\[1.5ex] dx+ey+fz=\color{red}\bm{k} \\[1.5ex] gx+hy+iz = \color{red}\bm{l} \end{cases}$

La matrice A e la matrice estesa A’ del sistema sono:

$\displaystyle A= \left( \begin{array}{ccc} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} a & b & c & \color{red}\bm{j} \\[1.1ex] d & e & f & \color{red}\bm{k} \\[1.1ex] g & h & i & \color{red}\bm{l} \end{array} \right)$

La regola di Cramer afferma che la soluzione di un sistema di equazioni è:

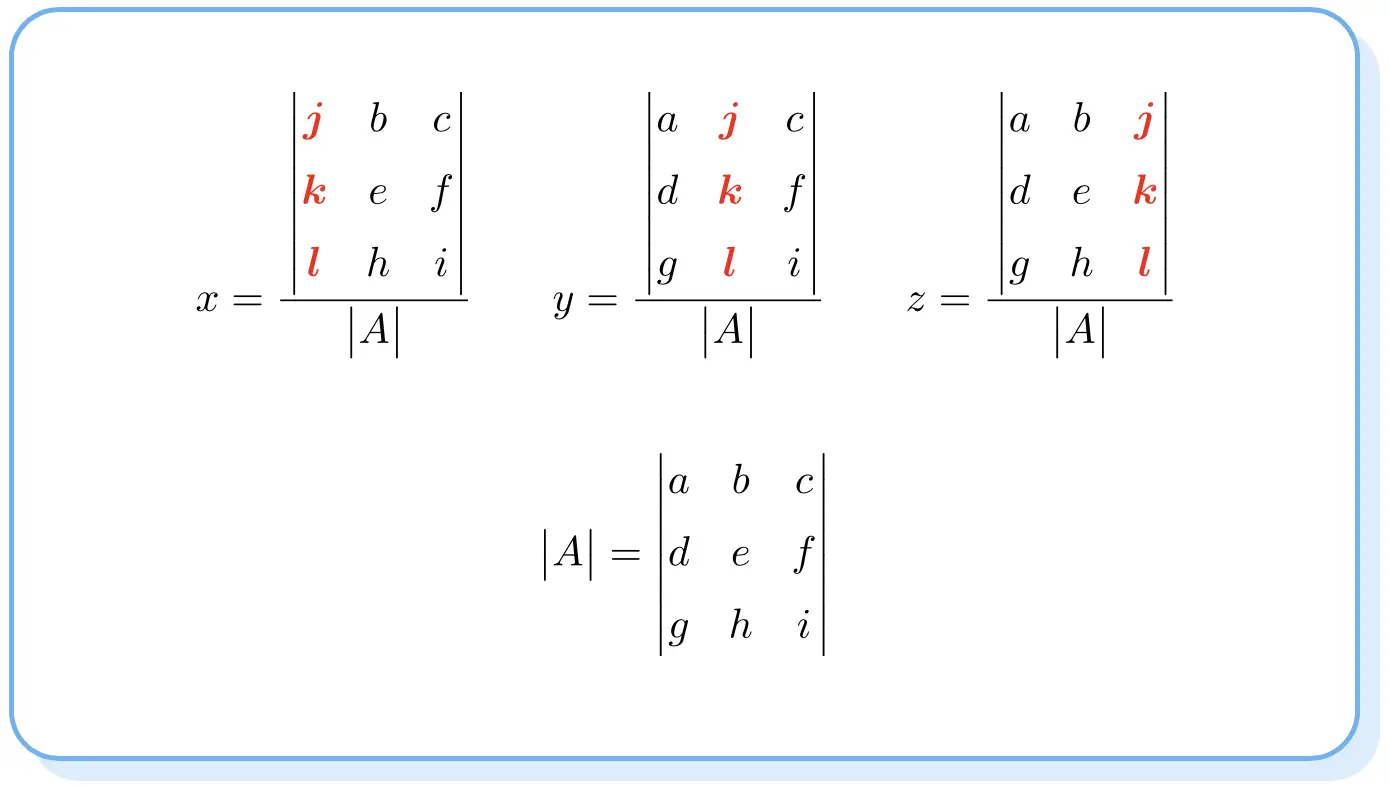
cos'è la regola di Cramer, spiegazione della regola di Cramer

Si noti che i determinanti dei numeratori sono come il determinante della matrice A ma cambiando la colonna di ciascuna incognita nella colonna dei termini indipendenti.

Pertanto, la regola di Cramer viene utilizzata per risolvere sistemi di equazioni lineari. Ma, come già sai, ci sono molti modi per risolvere un sistema di equazioni, ad esempio il metodo di Gauss Jordan è ben noto.

Di seguito sono riportati esempi di risoluzione di sistemi di equazioni lineari con la regola di Cramer, o talvolta anche scritti come regola di Kramer.

Esempio 1: sistema compatibile determinato (SCD)

Risolvi il seguente sistema di 3 equazioni in 3 incognite utilizzando la regola di Cramer:

$\begin{cases} 2x+y+3z= 1 \\[1.5ex] 3x-2y-z=0 \\[1.5ex] x+3y+2z = 5\end{cases}$

Per prima cosa realizziamo la matrice A e la matrice estesa A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & 1 \\[1.1ex] 3 & -2 & -1 & 0 \\[1.1ex] 1 & 3 & 2 & 5 \end{array} \right)$

Calcoliamo ora il rango delle due matrici, per vedere di che tipo di sistema si tratta. Per calcolare il rango di A, calcoliamo il determinante 3×3 dell’intera matrice (usando la regola di Sarrus) e vediamo se dà 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =-8-1+27+6+6-6 = 24 \neq 0$

Il determinante di A è diverso da 0, quindi la matrice A ha rango 3.

$\displaystyle rg(A)=3$

Quindi anche la matrice A’ è di rango 3 , poiché non può essere di rango 4 e deve essere almeno dello stesso rango della matrice A.

$\displaystyle rg(A')=3$

L’estensione della matrice A è pari all’estensione della matrice A’ e al numero di incognite del sistema (3), quindi, per il teorema di Rouché-Frobenius , sappiamo che si tratta di un determinato sistema compatibile (SCD):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

Una volta che sappiamo che il sistema è una SCD, applichiamo la regola di Cramer per risolverlo. Per fare ciò ricordiamo che la matrice A, il suo determinante e la matrice A’ sono:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & -1 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & 2 & \color{red}\bm{5} \end{array} \right)$

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =24$

Per calcolare l’incognita

$\displaystyle x$

Con la regola di Cramer, sostituiamo la prima colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} \color{red}\bm{1} & 1 & 3 \\[1.1ex] \color{red}\bm{0} & -2 & -1 \\[1.1ex] \color{red}\bm{5} & 3 & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{24}{24} = \bm{1}$

Per calcolare l’incognita

$\displaystyle y$

Con la regola di Cramer, sostituiamo la seconda colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 2 & \color{red}\bm{1} & 3 \\[1.1ex] 3 & \color{red}\bm{0} & -1 \\[1.1ex] 1 & \color{red}\bm{5} & 2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{48}{24} = \bm{2}$

Calcolare

$\displaystyle z$

Con la regola di Cramer, sostituiamo la terza colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 2 & 1 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & \color{red}\bm{5}\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-24}{24} = \bm{-1}$

La soluzione del sistema di equazioni è quindi:

$\displaystyle \bm{x = 1 \qquad y=2 \qquad z = -1}$

Esempio 2: sistema compatibile indeterminato (ICS)

Risolvi il seguente sistema di equazioni utilizzando la regola di Cramer:

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex] x+5y+3z = 1 \end{cases}$

Per prima cosa realizziamo la matrice A e la matrice estesa A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & 2 & 4 & 1 \\[1.1ex] -2 & 3 & -1 & 0 \\[1.1ex] 1 & 5 & 3 & 1 \end{array} \right)$

Ora calcoliamo il range delle due matrici e quindi possiamo vedere di che tipo di sistema si tratta. Per calcolare il rango di A, calcoliamo il determinante dell’intera matrice (usando la regola di Sarrus) e controlliamo se è 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3\end{vmatrix} = 27-2-40-12+15+12= 0$

Il determinante dà 0, quindi la matrice A non è di rango 3. Ma ha un determinante 2×2 diverso da 0:

$\displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0$

Quindi la matrice A ha rango 2 :

$\displaystyle rg(A)=2$

Una volta conosciuta l’estensione della matrice A, calcoliamo quella della matrice A’. Il determinante delle prime 3 colonne dà 0, quindi proviamo gli altri possibili determinanti 3×3 nella matrice A’:

$\displaystyle \begin{vmatrix} 2 & 4 & 1 \\[1.1ex] 3 & -1 & 0 \\[1.1ex] 5 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 4 & 1 \\[1.1ex] -2 & -1 & 0 \\[1.1ex] 1 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 2 & 1 \\[1.1ex] -2 & 3 & 0 \\[1.1ex] 1 & 5 & 1 \end{vmatrix} = 0$

Tutti i determinanti di ordine 3 danno 0. Ma, ovviamente, la matrice A’ ha lo stesso determinante 2×2 non 0 della matrice A:

$\displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0$

Pertanto anche la matrice A’ è di rango 2 :

$\displaystyle rg(A')=2$

Quindi, poiché il rango della matrice A è uguale al rango della matrice A’ ma questi due sono inferiori al numero di incognite del sistema (3), sappiamo dal teorema di Rouché-Frobenius che è Questo è un sistema indeterminatamente compatibile (ICS):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

Quando vogliamo risolvere un sistema indeterminato compatibile (SCI), dobbiamo trasformare il sistema : prima eliminiamo un’equazione, poi convertiamo una variabile in λ (solitamente la variabile z), e infine mettiamo insieme i termini con λ con i termini indipendenti.

Una volta trasformato il sistema applichiamo la regola di Cramer e otterremo la soluzione del sistema in funzione di λ.

In questo caso elimineremo l’ultima equazione dal sistema:

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex]\cancel{x+5y+3z = 1} \end{cases} \longrightarrow \quad \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0\end{cases}$

Ora convertiamo la variabile z in λ:

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x+2y+4\lambda=1 \\[1.5ex] -2x+3y-\lambda=0\end{cases}$

E mettiamo i termini con λ con i termini indipendenti:

$\begin{cases} 3x+2y=1-4\lambda \\[1.5ex] -2x+3y=\lambda \end{cases}$

Pertanto la matrice A e la matrice A’ del sistema restano:

$\displaystyle A= \left( \begin{array}{ccc} 3 & 2 \\[1.1ex] -2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & 2 & 1 -4\lambda \\[1.1ex] -2 & 3 & \lambda \end{array} \right)$

Infine, una volta trasformato il sistema, applichiamo la regola di Cramer . Risolviamo quindi il determinante di A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3\end{vmatrix} = 13$

Per calcolare l’incognita

$\displaystyle x$

Con la regola di Cramer, sostituiamo la prima colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1 -4\lambda & 2 \\[1.1ex] \lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3(1-4\lambda) -2\lambda}{13} = \cfrac{\bm{3-14\lambda} }{\bm{13}}$

Per calcolare l’incognita

$\displaystyle y$

Con la regola di Cramer, sostituiamo la seconda colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 1 -4\lambda \\[1.1ex]-2& \lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3\lambda -\bigl(-2(1-4\lambda)\bigr)}{13}= \cfrac{3\lambda -\bigl(-2+8\lambda\bigr)}{13} = \cfrac{\bm{2-5\lambda} }{\bm{13}}$

Mentre la soluzione del sistema di equazioni è funzione di λ, poiché è uno SCI e, quindi, ha infinite soluzioni:

$\displaystyle \bm{x =} \cfrac{\bm{3-14\lambda} }{\bm{13}} \qquad \bm{y=}\cfrac{\bm{2-5\lambda} }{\bm{13}} \qquad \bm{z = \lambda}$

La regola di Cramer ha risolto i problemi

Esercizio 1

Applica la regola di Cramer per risolvere il seguente sistema di due equazioni in 2 incognite:

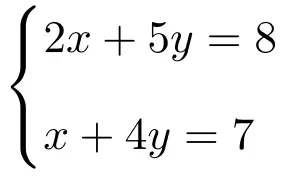
esercizio risolto passo dopo passo con la regola 2x2 di Cramer

vedi soluzione

La prima cosa da fare è la matrice A e la matrice estesa A’ del sistema:

$\displaystyle A= \left( \begin{array}{cc} 2 & 5 \\[1.1ex] 1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 2 & 5 & 8 \\[1.1ex] 1 & 4 & 7 \end{array}\right)$

Dobbiamo ora trovare il rango della matrice A. Per fare ciò controlliamo se il determinante dell’intera matrice è diverso da 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-5=3 \bm{\neq 0}$

Poiché la matrice ha un determinante 2×2 diverso da 0, la matrice A ha rango 2:

$\displaystyle rg(A)=2$

Una volta conosciuto il rango di A, calcoliamo il rango di A’. Questo sarà almeno di rango 2, perché abbiamo appena visto che ha al suo interno un determinante di ordine 2 diverso da 0. Inoltre, non può essere di rango 3, poiché non possiamo fare a meno di un determinante 3×3. Pertanto anche la matrice A’ è di rango 2:

$\displaystyle rg(A')=2$

Pertanto, applicando il teorema di Rouché-Frobenius, sappiamo che questo è un sistema determinato compatibile (SCD), perché l’intervallo di A è uguale all’intervallo di A’ e al numero di incognite.

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 2 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 2 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

Una volta che sappiamo che il sistema è una SCD, applichiamo la regola di Cramer per risolverlo.

Per calcolare l’incognita

$\displaystyle x$

Con la regola di Cramer, sostituiamo la prima colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 \\[1.1ex] 7 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-3}{3} = \bm{-1}$

Per calcolare l’incognita

$\displaystyle y$

Con la regola di Cramer, sostituiamo la seconda colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}2 & 8 \\[1.1ex] 1 & 7\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{6}{3} = \bm{2}$

La soluzione del sistema di equazioni è quindi:

$\displaystyle \bm{x = -1 \qquad y=2}$

Esercizio 2

Trova la soluzione del seguente sistema di tre equazioni in 3 incognite utilizzando la regola di Cramer:

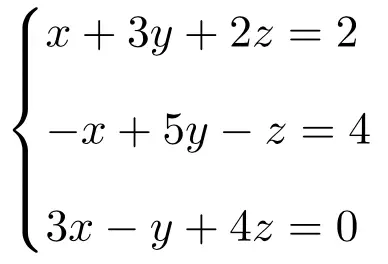
Esercizio risolto della regola di Cramer di un sistema di equazioni 3x3

vedi soluzione

Per prima cosa realizziamo la matrice A e la matrice estesa A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 3 & 2\\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 3 & 2 & 2 \\[1.1ex] -1 & 5 & -1 & 4 \\[1.1ex] 3 & -1 & 4 & 0 \end{array}\right)$

Troviamo ora il rango della matrice A calcolando il determinante della matrice 3×3 con la regola di Sarrus:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{vmatrix} = 20-9+2-30-1+12=-6 \bm{\neq 0}$

La matrice avente un determinante di ordine 3 diverso da 0, la matrice A è di rango 3:

$\displaystyle rg(A)=3$

di conseguenza anche la matrice A’ è di rango 3:

$\displaystyle rg(A')=3$

Pertanto, utilizzando il teorema di Rouché-Frobenius, sappiamo che questo è un sistema determinato compatibile (SCD), perché l’intervallo di A è uguale all’intervallo di A’ e al numero di incognite.

Una volta che sappiamo che il sistema è una SCD, dobbiamo applicare la regola di Cramer per risolverlo.

Per calcolare l’incognita

$\displaystyle x$

Con la regola di Cramer, sostituiamo la prima colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 & 3 & 2 \\[1.1ex] 4 & 5 & -1\\[1.1ex]0 & -1 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-18}{-6} = \bm{3}$

Per calcolare l’incognita

$\displaystyle y$

Con la regola di Cramer, sostituiamo la seconda colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 4 & -1\\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-6}{-6} = \bm{1}$

Calcolare

$\displaystyle z$

Con la regola di Cramer, sostituiamo la terza colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 3 & -1 & 0\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12}{-6} = \bm{-2}$

La soluzione del sistema di equazioni è quindi:

$\displaystyle \bm{x =3 \qquad y=1 \qquad z=-2}$

Esercizio 3

Calcola la soluzione del seguente sistema di tre equazioni in 3 incognite utilizzando la regola di Cramer:

vedi soluzione

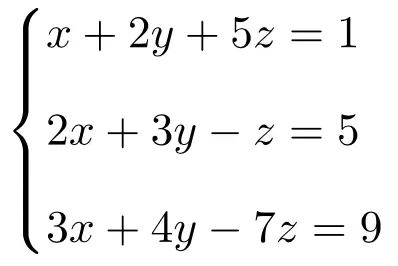
Per prima cosa realizziamo la matrice A e la matrice estesa A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 2 & 5 & 1 \\[1.1ex] 2 & 3 & -1 & 5 \\[1.1ex] 3 & 4 & -7 & 9 \end{array}\right)$

Calcoliamo l’estensione della matrice A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{vmatrix} =-21-6+40-45+4+28=0$

$\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0$

$\displaystyle rg(A)=2$

$\displaystyle \begin{vmatrix} 2 & 5 & 1 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 4 & -7 & 9 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 5 & 1 \\[1.1ex] 2 & -1 & 5 \\[1.1ex] 3 & -7 & 9\end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 1 \\[1.1ex] 2 & 3 & 5 \\[1.1ex] 3 & 4 & 9 \end{vmatrix} = 0$

Tutti i determinanti di ordine 3 danno 0. Tuttavia, la matrice A’ ha lo stesso determinante 2×2 non 0 della matrice A:

$\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0$

Pertanto anche la matrice A’ è di rango 2:

$\displaystyle rg(A')=2$

Poiché il rango della matrice A è uguale al rango della matrice A’ ma questi due sono inferiori al numero di incognite del sistema (3), sappiamo dal teorema di Rouché-Frobenius che si tratta di un sistema compatibile indeterminato (ICS):

Essendo un sistema ICS, dobbiamo eliminare un’equazione. In questo caso elimineremo l’ultima equazione dal sistema:

$\begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \\[1.5ex]\cancel{3x+4y-7z = 9} \end{cases} \longrightarrow \quad \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5\end{cases}$

Ora convertiamo la variabile z in λ:

$\begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+2y+5\lambda=1 \\[1.5ex] 2x+3y-\lambda=5\end{cases}$

E mettiamo i termini con λ con i termini indipendenti:

$\begin{cases} x+2y=1-5\lambda\\[1.5ex] 2x+3y=5+\lambda \end{cases}$

Tali che la matrice A e la matrice A’ del sistema rimangono:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 \\[1.1ex] 2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 2 & 1 -5\lambda \\[1.1ex] 2 & 3 &5+\lambda \end{array} \right)$

Infine, una volta trasformato il sistema, applichiamo la regola di Cramer . Risolviamo quindi il determinante di A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3\end{vmatrix} =-1$

Per calcolare l’incognita

$\displaystyle x$

Con la regola di Cramer, sostituiamo la prima colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1-5\lambda & 2 \\[1.1ex] 5+\lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3-15\lambda -(10+2\lambda)}{-1} = \cfrac{-7-17\lambda}{-1} = \bm{7+17\lambda}$

Per calcolare l’incognita

$\displaystyle y$

Con la regola di Cramer, sostituiamo la seconda colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 1-5\lambda \\[1.1ex] 2 & 5+\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{5+\lambda -(2-10\lambda)}{-1}= \cfrac{3+11\lambda}{-1} = \bm{-3-11\lambda}$

Mentre la soluzione del sistema di equazioni è funzione di λ, poiché è uno SCI e, quindi, ha infinite soluzioni:

$\displaystyle \bm{x =7+17\lambda} \qquad \bm{y=-3-11\lambda} \qquad \bm{z = \lambda}$

Esercizio 4

Risolvi il seguente problema di un sistema di tre equazioni in 3 incognite applicando la regola di Cramer:

$\begin{cases} -2x+5y+z=8 \\[1.5ex] 6x+2y+4z=4 \\[1.5ex] 3x-2y+z = -2 \end{cases}$

vedi soluzione

Per prima cosa costruiamo la matrice A e la matrice estesa A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc}-2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} -2 & 5 & 1 & 8 \\[1.1ex] 6 & 2 & 4 & 4 \\[1.1ex] 3 & -2 & 1 & -2 \end{array}\right)$

Calcoliamo ora il rango della matrice A calcolando il determinante della matrice 3×3 utilizzando la regola di Sarrus:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} -2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1 \end{vmatrix} = -4+60-12-6-16-30=-8 \bm{\neq 0}$

La matrice avente un determinante di ordine 3 diverso da 0, la matrice A è di rango 3:

$\displaystyle rg(A)=3$

di conseguenza, anche la matrice A’ è di rango 3, poiché deve essere almeno dello stesso rango della matrice A e non può essere di rango 4 perché è una matrice di dimensione 3×4.

$\displaystyle rg(A')=3$

Pertanto, utilizzando il teorema di Rouché-Frobenius, deduciamo che si tratta di un determinato sistema compatibile (SCD), perché l’intervallo di A è uguale all’intervallo di A’ e al numero di incognite.

Una volta che sappiamo che il sistema è una SCD, dobbiamo applicare la regola di Cramer per risolverlo.

Per calcolare l’incognita

$\displaystyle x$

Con la regola di Cramer, sostituiamo la prima colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 & 1 \\[1.1ex] 4 & 2 & 4 \\[1.1ex] -2 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{16}{-8} = \bm{-2}$

Per calcolare l’incognita

$\displaystyle y$

Con la regola di Cramer, cambiamo la seconda colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}-2 & 8 & 1 \\[1.1ex] 6 & 4 & 4 \\[1.1ex] 3 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-6} = \bm{0}$

Calcolare

$\displaystyle z$

Con la regola di Cramer, sostituiamo la terza colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} -2 & 5 & 8 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & -2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-32}{-8} = \bm{4}$

La soluzione del sistema di equazioni lineari è quindi:

$\displaystyle \bm{x =-2 \qquad y=0 \qquad z=4}$

Esercizio 5

Risolvi il seguente sistema di equazioni lineari utilizzando la regola di Cramer:

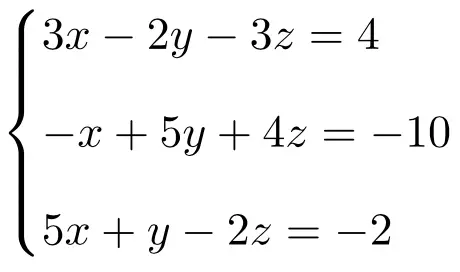
Esempio di risoluzione di un sistema di equazioni con la regola di Cramer

vedi soluzione

Per prima cosa realizziamo la matrice A e la matrice estesa A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -2 & -3 & 4 \\[1.1ex] -1 & 5 & 4 & -10 \\[1.1ex] 5 & 1 & -2 & -2 \end{array}\right)$

Calcoliamo l’estensione della matrice A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{vmatrix} =-30-40+3+75-12+4=0$

$\displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 15- (2)= 13 \neq 0$

$\displaystyle rg(A)=2$

$\displaystyle \begin{vmatrix} -2 & -3 & 4 \\[1.1ex] 5 & 4 & -10 \\[1.1ex] 1 & -2 & -2 \end{vmatrix} = 0 \qquad \begin{vmatrix}3 & -3 & 4 \\[1.1ex] -1 & 4 & -10 \\[1.1ex] 5 & -2 & -2\end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & -2 & 4 \\[1.1ex] -1 & 5 & -10 \\[1.1ex] 5 & 1 &-2\end{vmatrix} = 0$

Tutti i determinanti di ordine 3 danno 0. Ma, ovviamente, la matrice A’ ha lo stesso determinante di ordine 2 diverso da 0 della matrice A:

$\displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 13 \neq 0$

Pertanto anche la matrice A’ è di rango 2:

$\displaystyle rg(A')=2$

Il rango della matrice A è uguale al rango della matrice A’ ma questi due sono inferiori al numero di incognite del sistema (3), quindi dal teorema di Rouché-Frobenius sappiamo che è un Sistema Indeterminato Compatibile (SCI) :

Essendo un sistema ICS, dobbiamo eliminare un’equazione. In questo caso elimineremo l’ultima equazione dal sistema:

$\begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \\[1.5ex]\cancel{5x+y-2z = -2} \end{cases} \longrightarrow \quad \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10\end{cases}$

Ora convertiamo la variabile z in λ:

$\begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x-2y-3\lambda=4 \\[1.5ex] -x+5y+4\lambda=-10\end{cases}$

E mettiamo i termini con λ con i termini indipendenti:

$\begin{cases} 3x-2y=4+3\lambda \\[1.5ex] -x+5y=-10-4\lambda\end{cases}$

Tali che la matrice A e la matrice A’ del sistema rimangono:

$\displaystyle A= \left( \begin{array}{ccc} 3 & -2 \\[1.1ex] -1 & 5 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & -2 & 4+3\lambda \\[1.1ex] 1 & 5 &-10-4\lambda \end{array} \right)$

Infine, una volta trasformato il sistema, applichiamo la regola di Cramer . Risolviamo quindi il determinante di A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}3& -2 \\[1.1ex] -1 & 5\end{vmatrix} =13$

Per calcolare l’incognita

$\displaystyle x$

Con la regola di Cramer, sostituiamo la prima colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 4+3\lambda & -2 \\[1.1ex]-10-4\lambda & 5\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{20+15\lambda -(20+8\lambda)}{13} = \cfrac{\bm{7\lambda}}{\bm{13}}$

Per calcolare l’incognita

$\displaystyle y$

Con la regola di Cramer, cambiamo la seconda colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 4+3\lambda \\[1.1ex] -1 & -10-4\lambda\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-30-12\lambda -(-4-3\lambda)}{13}= \cfrac{\bm{-26-9\lambda}}{\bm{13}}$

Pertanto, la soluzione del sistema di equazioni è una funzione di λ, poiché è uno SCI e, quindi, il sistema ha infinite soluzioni:

$\displaystyle \bm{x=} \cfrac{\bm{7\lambda}}{\bm{13}} \qquad \bm{y=} \cfrac{\bm{-26-9\lambda}}{\bm{13}} \qquad \bm{z = \lambda}$

Regola di cramer

Qual è la regola di Cramer?

Esempio 1: sistema compatibile determinato (SCD)

Esempio 2: sistema compatibile indeterminato (ICS)

La regola di Cramer ha risolto i problemi

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Lascia un commento Annulla risposta