Punti complanari (o complanari)

In questa pagina scoprirai cosa sono i punti complanari (o complanari) e come sapere se determinati punti sono complanari o meno. Inoltre, potrai vedere esempi ed esercitarti con esercizi sui punti complanari risolti.

Cosa sono i punti complanari?

In geometria analitica il significato dei punti complanari (o complanari) è il seguente:

I punti complanari sono punti che appartengono allo stesso piano.

Pertanto, 2 o 3 punti sono sempre complanari perché un piano può essere formato anche con soli 3 punti. Quando invece i punti sono 4, 5 o più, è possibile che alcuni punti non siano contenuti nello stesso piano e, quindi, non siano complanari.

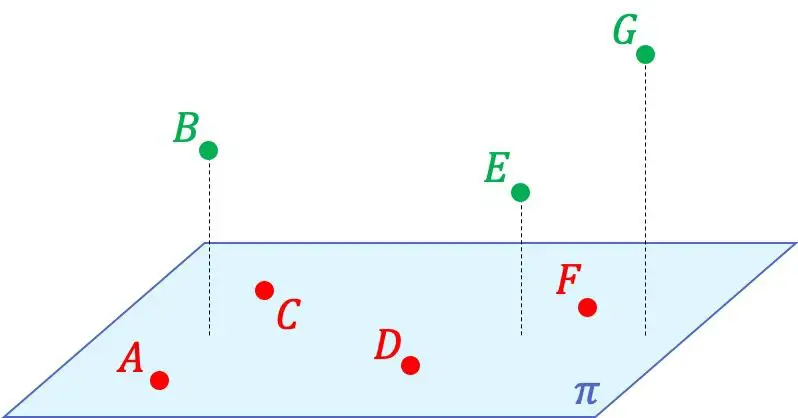
Ad esempio, nella rappresentazione grafica qui sopra, puoi vedere che i punti A, C, D e F sono complanari tra loro, poiché sono contenuti nello stesso piano. D’altra parte questi 4 punti non sono complanari ai punti B, E e G, perché nello spazio che contiene tutti i punti non si può formare alcun piano.

Da questa proprietà si deduce che i vettori definiti da punti complanari sono anche vettori complanari, cioè sono contenuti nello stesso piano.

Quando i punti sono complanari?

Come abbiamo visto nella definizione di punti complanari (o complanari), due o tre punti sono sempre complanari, ma non è necessario che più di tre punti rispettino il rapporto di complanarità.

Quindi, ci sono principalmente 2 metodi per determinare se quattro o più punti sono complanari:

Un modo per sapere se i punti sono complanari è tramite i vettori determinati dai punti: se questi vettori sono complanari , anche i punti sono complanari.

Ovviamente per applicare questo metodo è necessario sapere quando i vettori sono complanari. Ma poiché esistono anche diversi modi per determinare se un insieme di vettori è complanare, ti consigliamo di verificare come determinare se i vettori sono complanari . Qui troverai tutte le procedure esistenti per trovare quando 2, 3, 4 o più vettori sono complanari, oltre ad esempi ed esercizi risolti.

Un altro modo per sapere se un insieme di punti è complanare è trovare l’equazione del piano formato da 3 punti nell’insieme, e se gli altri punti soddisfano questa equazione, allora ciò significa che tutti i punti nell’insieme sono complanari.

Anche se dipende dal problema, consigliamo di utilizzare il primo dei due metodi, perché è molto più semplice e veloce verificare se i vettori sono complanari che calcolare l’equazione di un piano. Ma ovviamente usa quello che preferisci.

Risolti problemi di punti complanari

Esercizio 1

Determina se i seguenti tre punti sono complanari:

$A(3,5,1)$

$B(0,-2,3)$

$C(4,-1,2)$

vedi soluzione

In questo caso non è necessario fare alcun calcolo perché 3 punti sono sempre complanari , qualunque essi siano.

Esercizio 2

Determina se i seguenti quattro punti sono complanari:

$A(1,2,0)$

$B(-1,3,4)$

$C(1,0,-1)$

$D(2,5,-3)$

vedi soluzione

Affinché i quattro punti siano complanari, i vettori da essi determinati devono essere complanari. Calcoliamo quindi questi vettori:

$\vv{AB} = B- A = (-1,3,4)-(1,2,0) = (-2,1,4)$

$\vv{AC} = C- A = (1,0,-1)-(1,2,0) = (0,-2,-1)$

$\vv{AD} = D- A = (2,5,-3)-(1,2,0) = (1,3,-3)$

Costruiamo ora la matrice formata dai vettori:

$\displaystyle A= \begin{pmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{pmatrix}$

Affinché i vettori risultanti siano complanari, il rango della matrice precedente deve essere uguale a 2. E, per questo, il determinante dell’intera matrice 3×3 deve essere uguale a zero:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{vmatrix} =-11\neq 0$

$rg(A)=3$

Tuttavia il determinante dell’intera matrice è diverso da zero, quindi il rango della matrice è 3, e quindi i 4 punti non sono complanari .

Esercizio 3

Scopri se i seguenti cinque punti sono complanari:

$A(3,1,1)$

$B(0,0,2)$

$C(4,-2,-1)$

$D(-1,1,3)$

$E(2,4,3)$

vedi soluzione

Affinché tutti e cinque i punti siano complanari, i vettori da essi definiti devono essere complanari. Calcoliamo quindi questi vettori:

$\vv{AB} = B- A = (0,0,2)-(3,1,1) = (-3,-1,1)$

$\vv{AC} = C- A = (4,-2,-1)-(3,1,1) = (1,-3,-2)$

$\vv{AD} = D- A = (-1,1,3)-(3,1,1) = (-4,0,2)$

$\vv{AE} = E- A = (2,4,3)-(3,1,1) = (-1,3,2)$

Costruiamo ora la matrice composta dai vettori:

$\displaystyle A= \begin{pmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{pmatrix}$

Affinché i vettori risultanti siano complanari, il rango della matrice precedente deve essere uguale a 2. Calcoliamo quindi il rango della matrice dei vettori mediante determinanti per verificare se sono complanari:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\end{vmatrix} = 0 \qquad \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -1&3&2\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0 \qquad \begin{vmatrix} 1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} -3&-1 \\[1.1ex] 1&-3\end{vmatrix} =10\neq 0$

$rg(A)=2$

Il rango della matrice è equivalente a 2, quindi i vettori sono complanari e quindi sono complanari anche i 5 punti.

Esercizio 4

Calcolare il valore del parametro

$k$

in modo che i seguenti 4 punti siano complanari:

$A(3,1,4)$

$B(2,1,2)$

$C(0,-1,3)$

$D(3,2,k)$

vedi soluzione

Affinché i quattro punti siano complanari, i vettori da essi determinati devono essere complanari. Calcoliamo quindi questi vettori:

$\vv{AB} = B- A = (2,1,2)-(3,1,4) = (-1,0,-2)$

$\vv{AC} = C- A = (0,-1,3)-(3,1,4) = (-3,-2,-1)$

$\vv{AD} = D- A = (3,2,k)-(3,1,4) = (0,1,k-4)$

La cui matrice vettoriale è:

$\displaystyle A= \begin{pmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{pmatrix}$

Affinché i vettori risultanti siano complanari, il rango della matrice deve essere 2. E, quindi, il determinante dell’intera matrice 3×3 deve essere 0:

$\displaystyle \begin{vmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{vmatrix} =0$

$\displaystyle 2k-3 =0$

Infine, risolviamo l’ignoto

$k:$

$2k =3$

$\bm{k =}\mathbf{\cfrac{3}{2}}$

Infine, se questo articolo ti è stato utile, probabilmente ti interesserà anche come viene calcolata la distanza tra due punti (formula) , poiché a volte nei problemi di geometria analitica ci viene chiesto qual è la distanza tra due punti. Nella pagina collegata troverai una spiegazione molto dettagliata, oltre ad esempi ed esercizi risolti passo dopo passo.

Punti complanari (o complanari).

Cosa sono i punti complanari?

Quando i punti sono complanari?

Risolti problemi di punti complanari

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Lascia un commento Annulla risposta