▷ Come faccio a sapere se 3 (o più) punti sono allineati? ✅

In questa pagina troverai la spiegazione di cosa sono i punti allineati. Vedrai anche tutti i metodi disponibili per determinare se 3 (o più) punti sono allineati. E in più troverai numerosi esempi e anche esercizi risolti per poterti esercitare.

Cosa significa che i punti sono allineati?

Nella geometria analitica tre o più punti sono allineati se si trovano tutti sulla stessa linea, cioè se possono essere uniti tracciando tra loro una linea retta.

Ovviamente, 2 punti saranno sempre allineati, poiché puoi sempre tracciare una linea tra due punti. Tuttavia, non è necessario che tre punti siano sulla stessa linea. Principalmente esistono due metodi per sapere se 3 o più punti sono allineati:

Metodo dei vettori : consiste nel vedere se i vettori che formano i punti sono proporzionali.
Metodo dell’equazione della linea : consiste nel determinare se i punti appartengono alla stessa linea.

Di seguito è riportata la spiegazione di ciascuna procedura ed esempi in modo che tu possa decidere quale è la migliore per te.

Come sapere se 3 (o più) punti sono allineati con il metodo vettoriale

Considerando tre punti:

$A(x_1,y_1) \quad B(x_2,y_2) \quad C(x_3,y_3)$

I tre punti sono allineati se i vettori

$\vv{AB}$

$\vv{BC}$

hanno lo stesso verso, cioè se le loro componenti sono proporzionali.

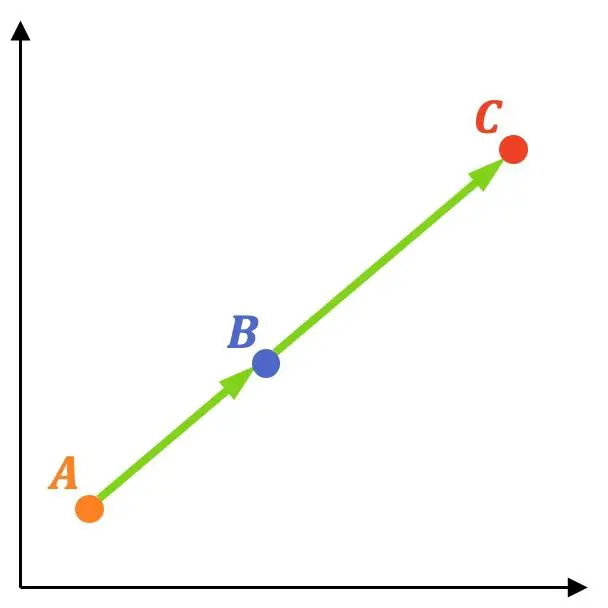
Vediamo un esempio di come si fa:

Determina se i seguenti 3 punti sono allineati:

$A(1,2) \quad B(4,4) \quad C(-2,0)$

Innanzitutto, calcoliamo i vettori tra i punti. È sufficiente calcolare due vettori diversi:

$\vv{AB} = B - A = (4,4)- (1,2) = (3,2)$

$\vv{BC} = C-B =(-2,0)- (4,4)= (-6,-4)$

E poi controlliamo se le coordinate dei vettori sono proporzionali:

$\cfrac{-6}{3} = \cfrac{-4}{2} = -2$

Dividendo le componenti X e le componenti Y dei due vettori otteniamo lo stesso risultato (-2), quindi i vettori hanno la stessa direzione e, quindi, i punti sono allineati .

Questo metodo può essere utilizzato anche per sapere se tre o più punti sono allineati nello spazio (in R3), l’unica cosa da aggiungere è verificare che anche la terza componente dei due vettori (componente Z) sia proporzionale.

Se questo articolo ti è utile, probabilmente ti interesserà anche sapere come calcolare il punto medio tra due punti , poiché, ovviamente, trovare il punto medio di 2 punti è un modo per determinare un terzo punto allineato con gli altri due punti. Puoi vedere come si fa nella pagina collegata, inoltre potrai anche vedere esempi ed esercizi risolti passo dopo passo.

Come sapere se 3 (o più) punti sono allineati con il metodo dell’equazione della linea retta

Come abbiamo appena visto nella sezione precedente, un modo per studiare l’allineamento di 3 o più punti è utilizzare i vettori che si possono formare tra di loro. Bene, un altro metodo è iniziare con l’equazione di una linea:

Considerando tre punti:

$A(x_1,y_1) \quad B(x_2,y_2) \quad C(x_3,y_3)$

I tre punti sono allineati se appartengono tutti alla stessa retta. Pertanto, per sapere se tre o più punti sono allineati, è necessario seguire i seguenti passaggi:

Trova l’equazione della retta che passa per due dei tre punti.
Controlla se anche il terzo punto appartiene alla linea. In questo caso significa che i 3 punti sono allineati, invece se la condizione non è soddisfatta significa che i punti non sono allineati.

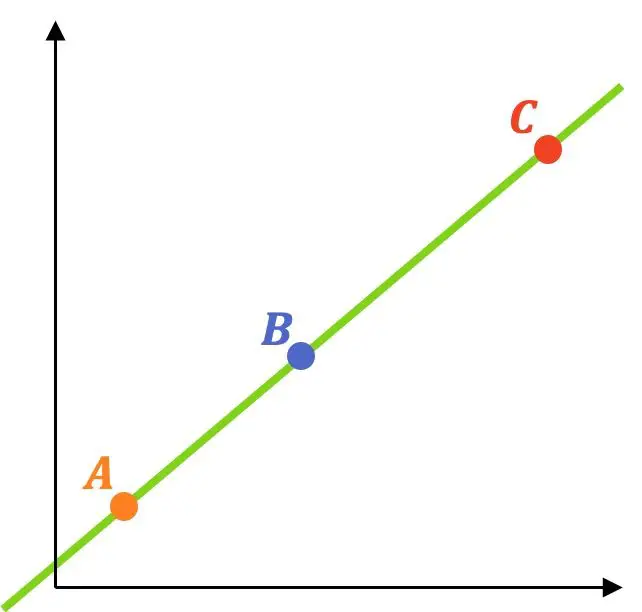
Ad esempio, risolveremo un esercizio utilizzando questo metodo:

Controlla che i seguenti 3 punti siano allineati:

$A(3,1) \quad B(1,4) \quad C(5,-2)$

Innanzitutto dobbiamo calcolare l’equazione della retta che passa per i punti A e B. Troviamo quindi il vettore direzione della retta:

$\vv{AB} = B-A = (1,4) - (3,1) = (-2,3)$

Ora devi costruire l’equazione della retta, puoi scegliere il tipo che preferisci: parametrica, implicita, generale, ecc. Ma in questo caso utilizzeremo l’equazione continua. Quindi l’equazione continua della retta che passa per il punto A e il punto B sarà:

$\cfrac{x-3}{-2}=\cfrac{y-1}{3}$

Una volta ottenuta l’equazione della retta, dobbiamo verificare se anche l’altro punto appartiene alla stessa retta. Per fare ciò, sostituiamo le coordinate del punto C nell’equazione della retta:

$\cfrac{5-3}{-2}=\cfrac{-2-1}{3}$

$\cfrac{2}{-2}=\cfrac{-3}{3}$

$-1=-1$

Abbiamo un pareggio, quindi il punto soddisfa l’equazione della linea. E quindi i 3 punti sono collineari .

Va notato che un insieme di punti allineati non deve essere necessariamente equidistante, cioè la distanza tra più punti allineati può essere diversa. Puoi vedere la differenza tra i due concetti nella spiegazione della distanza tra due punti (geometria) , dove puoi vedere anche esempi ed esercizi risolti passo dopo passo.

Esercizi con punti allineati risolti

Esercizio 1

Determina se i seguenti 3 punti sono allineati:

$A(1,1) \quad B(2,-1) \quad C(-2,7)$

Vedi la soluzione

Possiamo scegliere uno dei due metodi che abbiamo visto per risolvere il problema. In questo caso utilizzeremo il metodo vettoriale.

Innanzitutto, calcoliamo i vettori tra i punti:

$\vv{AB} = B - A = (2,-1)- (1,1) = (1,-2)$

$\vv{BC} = C-B =(-2,7)- (2,-1)= (-4,8)$

E ora controlliamo se le coordinate cartesiane dei vettori sono proporzionali:

$\cfrac{-4}{1} = \cfrac{8}{-2} = -4$

Dividendo tra loro le componenti X e le componenti Y dei due vettori otteniamo lo stesso risultato (-4), quindi i vettori hanno la stessa direzione. Fatto che indica che i punti sono allineati .

Esercizio 2

Dati 3 punti:

$A(6,3) \quad B(4,-3) \quad C(4,5)$

Determina quali si allineano con i seguenti due punti:

$D(3,-1) \quad E(2,1)$

Vedi la soluzione

In questo caso utilizzeremo il metodo dell’equazione della linea retta, quindi risparmieremo alcuni calcoli.

Calcoliamo quindi l’equazione continua della retta che passa per i punti D ed E:

$\vv{DE} = E-D = (2,1) - (3,-1) = (-1,2)$

$\cfrac{x-3}{-1}=\cfrac{y+1}{2}$

E ora controlliamo quali punti corrispondono all’equazione della retta, e quindi sono allineati con i punti D ed E, e quali no.

Controlliamo il punto A:

$\cfrac{6-3}{-1}=\cfrac{3+1}{2}$

$\cfrac{3}{-1}=\cfrac{4}{2}$

$-3\neq 2$

L’equazione della retta non è vera, quindi il punto A non è allineato con i punti D ed E.

Controlliamo ora il punto B:

$\cfrac{4-3}{-1}=\cfrac{-3+1}{2}$

$\cfrac{1}{-1}=\cfrac{-2}{2}$

$-1= -1$

In questo caso l’equazione della retta è soddisfatta, quindi il punto B è collineare ai punti D ed E.

E infine, ripetiamo il processo con il punto C:

$\cfrac{4-3}{-1}=\cfrac{5+1}{2}$

$\cfrac{1}{-1}=\cfrac{6}{2}$

$-1\neq 3$

L’equazione della retta non è vera, quindi il punto C non è allineato con i punti D ed E.

Esercizio 3

Trovare il valore dell’ignoto

$k$

in modo che i seguenti 3 punti siano allineati:

$A(k,5) \quad B(-1,-4) \quad C(k-1,2)$

Vedi la soluzione

In questo caso utilizzeremo il metodo vettoriale.

Proviamo quindi a calcolare i vettori tra i punti:

$\vv{AB} = B - A = (-1,-4)- (k,5) = (-1-k,-9)$

$\vv{BC} = C-B =(k-1,2)- (-1,-4)= (k,6)$

Affinché la collinearità a tre punti sia soddisfatta, le coordinate dei due vettori devono essere proporzionali. Applichiamo quindi questa condizione:

$\cfrac{-1-k}{k} = \cfrac{-9}{6}$