Prodotto misto di tre vettori (o prodotto triplo punto)

In questa pagina spieghiamo cos’è il prodotto misto di tre vettori (o prodotto triplo punto) e come viene calcolato. Vedrai anche esempi, esercizi e problemi risolti su questo tipo di operazione tra vettori. E in più troverai le proprietà e le applicazioni del prodotto miscelato.

Qual è il prodotto misto di tre vettori?

Il prodotto misto di tre vettori, chiamato anche prodotto triplo scalare , è una moltiplicazione successiva tra tre vettori che coinvolge due diversi tipi di operazioni: il prodotto scalare e il prodotto vettoriale . Quindi, la combinazione delle due operazioni vettoriali dà uno scalare (un numero reale).

Concretamente, il prodotto misto consiste nel calcolare il prodotto vettoriale di due vettori e, successivamente, moltiplicare vettorialmente il risultato ottenuto per un terzo vettore. Scritto così può sembrare molto complicato, ma in realtà non lo è poi così tanto, guarda la formula del prodotto triplo punto:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})$

Come puoi vedere nella sua formula, il prodotto misto di tre vettori è indicato da due parentesi quadre.

Come calcolare il prodotto misto di tre vettori?

La formula del prodotto triplo punto è quella che abbiamo appena visto nella sezione precedente, tuttavia, generalmente non viene utilizzata per determinare il prodotto misto di tre vettori perché esiste un altro modo, più semplice e veloce:

Siano 3 vettori qualsiasi:

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)\qquad \vv{\text{w}}= (\text{w}_x,\text{w}_y,\text{w}_z)$

Per calcolare il prodotto misto tra tre vettori è sufficiente risolvere il determinante 3×3 formato dalle componenti dei vettori:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \\[1.1ex] \text{w}_x & \text{w}_y & \text{w}_z \end{vmatrix}$

Quindi puoi vedere un esempio di come viene calcolato , troveremo il prodotto misto dei seguenti tre vettori:

$\vv{\text{u}}= (1,2,0) \qquad \vv{\text{v}}= (0,-1,3)\qquad \vv{\text{w}}= (-2,4,1)$

Per determinare il prodotto misto, costruiamo un determinante di ordine 3 posizionando i vettori in righe della matrice:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix}$

E ora dobbiamo solo risolvere il determinante della matrice, per questo puoi utilizzare qualsiasi metodo. In questo caso applicheremo la regola di Sarrus (ma si può fare anche per addizioni o cofattori):

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} \\[2ex] &= -1-12+0-0-12-0 \\[2ex] & = \bm{-25} \end{aligned}$

Per dimostrare che i due procedimenti sono equivalenti calcoleremo il prodotto misto degli stessi vettori mediante la loro definizione:

$\begin{aligned} \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] & = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})\\[2ex] &=(1,2,0) \cdot \Bigl( (0,-1,3)\times (-2,4,1)\Bigr) \\[2ex] & = (1,2,0) \cdot \begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 0& -1 & 3 \\[1.1ex] -2 &4&1 \end{vmatrix} \\[2ex] &= (1,2,0) \cdot (-13,-6,-2) \\[2ex] & = \bm{-25} \end{aligned}$

Si consiglia di calcolare il prodotto misto attraverso il determinante dei vettori, poiché è più veloce e ci sono meno possibilità di sbagliare. Ma, come puoi vedere, il risultato è lo stesso indipendentemente dal metodo che usi, quindi usa quello che preferisci. 👍

Interpretazione geometrica del prodotto misto

Una volta che sai come trovare il prodotto misto di tre vettori, potresti chiederti… e a cosa serve il prodotto misto? Ebbene, in matematica ha due usi principali: calcolare il volume di un parallelepipedo e il volume di un tetraedro.

Il volume di un parallelepipedo è pari al valore assoluto del prodotto misto dei vettori che segnano le 3 dimensioni del campo geometrico.

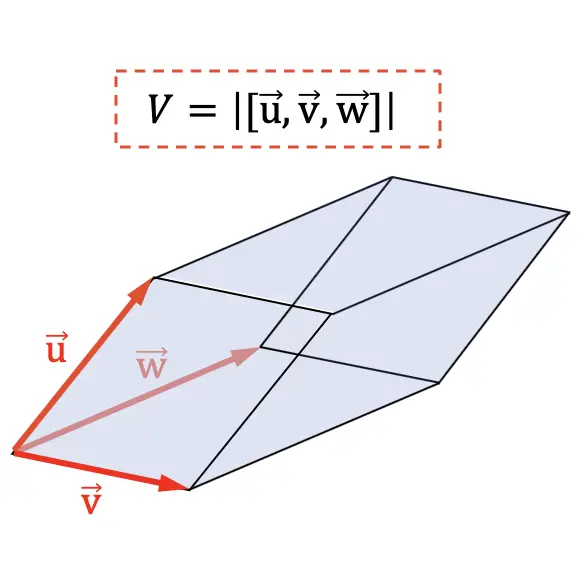
esempio di prodotto misto di tre vettori o prodotto scalare triplo

Un’altra applicazione del prodotto miscelato è determinare il volume di un tetraedro . Poiché geometricamente la sesta parte del valore assoluto del prodotto misto rappresenta il volume di un tetraedro:

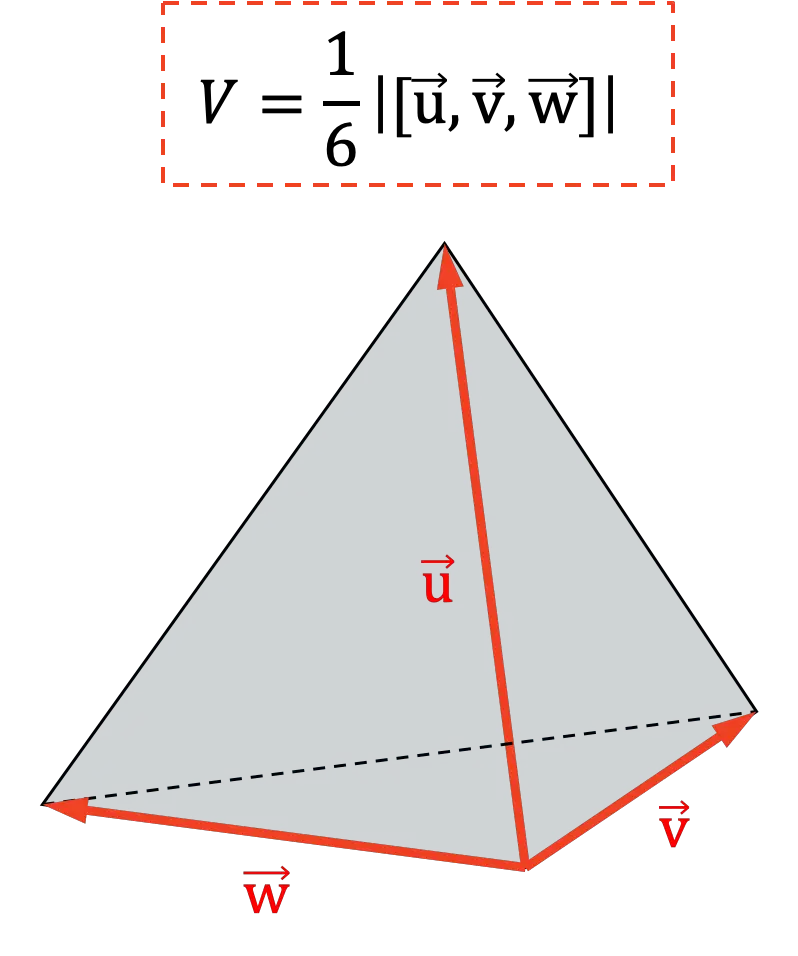
Proprietà del prodotto misto o del prodotto a tre punti

Il prodotto misto, o prodotto scalare triplo, ha le seguenti caratteristiche:

In generale, un cambiamento nell’ordine dei vettori dei prodotti misti implica anche un cambiamento di segno. Pertanto, l’ordine dei vettori dei prodotti misti è importante.

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = -\bigl[\vv{\text{v}},\vv{\text{u}},\vv{\text{w}}\bigr] = -\bigl[\vv{\text{u}},\vv{\text{w}},\vv{\text{v}}\bigr] = - \bigl[\vv{\text{w}},\vv{\text{v}},\vv{\text{u}}\bigr]$

Se però cambiamo ciclicamente l’ordine, il segno non cambia:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \bigl[\vv{\text{v}},\vv{\text{w}},\vv{\text{u}}\bigr] = \bigl[\vv{\text{w}},\vv{\text{u}},\vv{\text{v}}\bigr]$

In uno spazio tridimensionale (in R3), il prodotto misto di tre vettori linearmente dipendenti o complanari (appartenenti allo stesso piano) è uguale a 0.

Risolti i problemi relativi ai prodotti misti

Esercizio 1

Dati 3 vettori:

$\vv{\text{u}}= (3,-1,2) \qquad \vv{\text{v}}= (-2,0,1)\qquad \vv{\text{w}}= (5,1,-1)$

Calcola il prodotto misto dei tre vettori:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]$

vedi soluzione

Per trovare il suo prodotto misto, dobbiamo risolvere il determinante composto dalle coordinate dei vettori:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & -1 & 2 \\[1.1ex] -2 & 0 & 1 \\[1.1ex] 5 & 1 & -1 \end{vmatrix} \\[2ex] &= 0-5-4-0-3+2 \\[2ex] & = \bm{-10} \end{aligned}$

Esercizio 2

Dati 3 vettori:

$\vv{\text{u}}= (7,2,-3) \qquad \vv{\text{v}}= (2,4,9)\qquad \vv{\text{w}}= (4,3,-1)$

Determinare il prodotto misto tra i tre vettori:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]$

vedi soluzione

Per trovare il suo prodotto misto, dobbiamo risolvere il determinante che ha le coordinate cartesiane dei vettori in forma di linea:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 7 & 2 & -3 \\[1.1ex] 2 & 4 & 9 \\[1.1ex] 4 & 3 & -1 \end{vmatrix} \\[2ex] &= -28+72-18+48-189+4 \\[2ex] & = \bm{-111} \end{aligned}$

Esercizio 3

Calcola il volume del parallelepipedo i cui 3 lati sono i seguenti vettori:

$\vv{\text{u}}= (0,2,5) \qquad \vv{\text{v}}= (-1,6,2)\qquad \vv{\text{w}}= (3,1,2)$

vedi soluzione

Il volume di un parallelepipedo è uguale al valore assoluto del prodotto misto di 3 dei vettori che ha come spigoli. Pertanto, calcoliamo prima il triplo prodotto incrociato dei vettori:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 0 & 2 & 5 \\[1.1ex] -1 & 6 & 2 \\[1.1ex] 3 & 1 & 2 \end{vmatrix} \\[2ex] &= 0+12-5-90-0+4 \\[2ex] & = -79 \end{aligned}$

Quindi il volume del parallelepipedo è il valore assoluto del risultato del prodotto miscelato:

$V= \lvert -79 \rvert = \bm{79}\ \mathbf{u}\bm{^3}$

Esercizio 4

Calcola il volume del tetraedro i cui vertici sono i seguenti punti:

$A(1,0,2) \qquad B(3,3,2)\qquad C(5,-1,4)\qquad D(4,2,1)$

vedi soluzione

Per prima cosa calcoliamo i vettori che rappresentano i bordi del tetraedro:

$\vv{AB}=B-A= (3,3,2)-(1,0,2)=(2,3,0)$

$\vv{AC}=C-A= (5,-1,4)-(1,0,2)=(4,-1,2)$

$\vv{AD}=D-A= (4,2,1)-(1,0,2)=(3,2,-1)$

Il volume di un tetraedro equivale a un sesto del valore assoluto del prodotto misto di 3 dei vettori che ha per gli spigoli. Pertanto, calcoliamo prima il prodotto misto dei vettori trovati:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 2 & 3 & 0 \\[1.1ex] 4 & -1 & 2 \\[1.1ex] 3 & 2 & -1 \end{vmatrix} \\[2ex] &= 2+18+0-0-8+12 \\[2ex] & = 24 \end{aligned}$

Quindi il volume del tetraedro sarà un sesto del valore assoluto del prodotto misto:

$V= \cfrac{1}{6} \cdot \lvert 24 \rvert = \cfrac{24}{6} = \bm{4} \ \mathbf{u}\bm{^3}$

Qual è il prodotto misto di tre vettori?

Come calcolare il prodotto misto di tre vettori?

Interpretazione geometrica del prodotto misto

Proprietà del prodotto misto o del prodotto a tre punti

Risolti i problemi relativi ai prodotti misti

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Lascia un commento Annulla risposta