Matrice ortogonale

In questa pagina vedrai cosa sono le matrici ortogonali e la relazione che hanno con l’inversa di una matrice. Vedrai anche diversi esempi per capirlo perfettamente. Inoltre, ti insegniamo la formula che controlla qualsiasi matrice ortogonale, con la quale saprai trovarne una rapidamente. Ed infine troverete le proprietà e le applicazioni di queste particolari matrici oltre ad un tipico esercizio d’esame risolto.

Cos’è una matrice ortogonale?

La definizione di matrice ortogonale è la seguente:

Una matrice ortogonale è una matrice di numeri reali quadrati che moltiplicata per la sua trasposizione (o trasposizione) equivale alla matrice identità. Cioè, è soddisfatta la seguente condizione:

$A\cdot A^t = A^t \cdot A =I$

Oro

$A$

è una matrice ortogonale e

$A^t$

ne rappresenta la matrice trasposta.

Affinché questa condizione sia soddisfatta, le colonne e le righe di una matrice ortogonale devono essere vettori unitari ortogonali, cioè devono formare una base ortonormale. Per questo motivo alcuni matematici le chiamano anche matrici ortonormali .

Inversa di una matrice ortogonale

Un altro modo per spiegare il concetto di matrice ortogonale è attraverso la matrice inversa, perché la matrice trasposta (o trasposta) di una matrice ortogonale è uguale alla sua inversa.

Per comprendere appieno questo teorema, è importante sapere come invertire una matrice . In questo link troverai una spiegazione dettagliata dell’inverso di una matrice, tutte le sue proprietà e avrai anche degli esercizi risolti passo dopo passo con cui esercitarti.

Si può facilmente dimostrare che la matrice inversa di una matrice ortogonale è equivalente alla sua trasposta utilizzando la condizione di matrice ortogonale e la proprietà principale delle matrici inverse:

$\left.\begin{array}{c} A \cdot A^t =I \\[2ex] A \cdot A^{-1} = I\end{array} \right\} \longrightarrow \ A^t=A^{-1}$

Pertanto una matrice ortogonale sarà sempre una matrice invertibile , ovvero sarà una matrice regolare o non degenere.

Successivamente vedremo diversi esempi di matrici ortogonali per finire di comprendere il concetto di tutto.

Esempio di matrice ortogonale 2×2

La seguente matrice è una matrice ortogonale di dimensione 2×2:

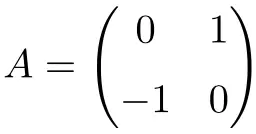
Possiamo verificare che è ortogonale calcolando il prodotto per la sua trasposta:

$\displaystyle A\cdot A^t$

$\displaystyle A\cdot A^t= \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Poiché il risultato dà la matrice Identica, verifichiamo che A è una matrice ortogonale.

Esempio di matrice ortogonale 3×3

La seguente matrice è una matrice ortogonale di dimensione 3×3:

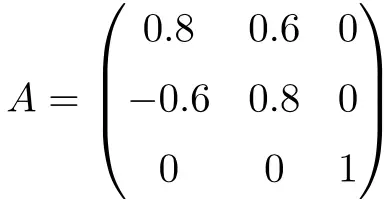
Possiamo dimostrare che è ortogonale moltiplicando la matrice A per la sua trasposta:

$\displaystyle A\cdot A^t = \begin{pmatrix}0.8&0.6&0\\[1.1ex] -0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}\cdot \begin{pmatrix}0.8&-0.6&0\\[1.1ex] 0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}= \begin{pmatrix} 1 & 0 & 0\\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0&0&1\end{pmatrix}$

Poiché la soluzione è la matrice unitaria, dimostriamo che A è una matrice ortogonale.

Formula per trovare una matrice ortogonale 2×2

Vedremo poi la dimostrazione che tutte le matrici ortogonali di ordine 2 seguono lo stesso schema.

Consideriamo una generica matrice di dimensione 2×2:

$\displaystyle A=\begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}$

Affinché questa matrice sia ortogonale, deve essere soddisfatta la seguente equazione di matrice:

$\displaystyle A\cdot A^t =I$

$\displaystyle \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix} \cdot \begin{pmatrix} a & c \\[1.1ex] b & d \end{pmatrix} =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Risolvendo la moltiplicazione di matrici, otteniamo le seguenti equazioni:

$\displaystyle \begin{pmatrix} a^2+b^2 & ac+bd \\[1.1ex] ac+bd & c^2+d^2 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\displaystyle \begin{array}{c}a^2+b^2=1 \\[2ex] ac+bd=0 \\[2ex] c^2+d^2=1 \end{array} \qquad \begin{array}{l} (1) \\[2ex] (2) \\[2ex] (3) \end{array}$

Se guardi da vicino, queste uguaglianze assomigliano molto alla fondamentale relazione trigonometrica pitagorica :

$\displaystyle \sin ^2\alpha+\cos ^2\alpha=1$

Di conseguenza, i termini che soddisfano le equazioni (1) e (3) ottenuti sono:

$\displaystyle \begin{array}{l} a = \cos \theta \qquad \qquad \qquad c = \sin\phi \\[2ex] b = \sin \theta \qquad \qquad \qquad d = \cos \phi\end{array}$

Inoltre, sostituendo i valori nella seconda equazione, otteniamo la relazione tra i due angoli:

$\displaystyle ac+bd=0$

$\displaystyle \cos\theta\sin\phi+\sin\theta\cos\phi=0$

$\displaystyle \tan\phi=-\tan\theta$

Cioè, deve essere soddisfatta una delle seguenti due condizioni:

$\displaystyle \text{si} \quad c=\sin\phi=-\sin\theta \quad \longrightarrow \quad d=\cos\phi=\cos\theta$

$\displaystyle \text{si} \quad d=\cos \phi=-\cos \theta \quad \longrightarrow \quad c=\sin\phi=\sin\theta$

Quindi, in conclusione, le matrici ortogonali devono avere la struttura di una delle due matrici seguenti:

formula per la matrice ortogonale di dimensione 2x2

Oro

$\theta$

è un numero reale.

Infatti, se ad esempio ne concediamo il valore

$\displaystyle\theta=\frac{\pi}{2}$

e prendiamo la prima struttura, otterremo la matrice che abbiamo verificato ortogonale nella sezione “Esempio di matrice ortogonale 2×2”:

$\displaystyle M_1 \left(\theta =\frac{\pi}{2}\right)=\begin{pmatrix} \cos \cfrac{\pi}{2} &\sin \cfrac{\pi}{2} \\[4ex] -\sin \cfrac{\pi}{2} & \cos \cfrac{\pi}{2} \end{pmatrix}=\begin{pmatrix} \vphantom{\frac{\pi}{2}}0 &1 \\[2ex]\vphantom{\frac{\pi}{2}} -1 & 0 \end{pmatrix}$

Proprietà della matrice ortogonale

Le caratteristiche di questo tipo di matrice sono:

Una matrice ortogonale non può mai essere una matrice singolare , perché può sempre essere invertita. In questo senso l’inverso di una matrice ortogonale è un’altra matrice ortogonale.

Qualsiasi matrice ortogonale può essere diagonalizzata. Diciamo allora che le matrici ortogonali sono ortogonalmente diagonalizzabili.

Tutti gli autovalori o autovalori di una matrice ortogonale hanno modulo pari a 1.

Anche qualsiasi matrice ortogonale composta solo da numeri reali è una matrice normale.

L’analogo della matrice ortogonale in un ambiente con numeri complessi è la matrice unitaria.

Ovviamente la matrice identità è una matrice ortogonale.

L’insieme delle matrici ortogonali di dimensione n × n nonché l’operazione del prodotto di matrici formano un gruppo chiamato gruppo ortogonale. Cioè il prodotto di due matrici ortogonali è uguale a un’altra matrice ortogonale.

Inoltre, il risultato della moltiplicazione di una matrice ortogonale per la sua trasposta può essere espresso dal delta di Kronecker:

$\displaystyle (A\cdot A^{t})_{ij} = \delta_{ij}=\begin{cases}1 & \mbox{si }i = j, \\[2ex] 0 & \mbox{si }i \ne j\end{cases}$

Infine, il determinante di una matrice ortogonale è sempre +1 o -1.

$\displaystyle \text{det}(A)=\pm 1$

Esercizio risolto di matrici ortogonali

Risolveremo poi un esercizio sulle matrici ortogonali.

Data la seguente matrice quadrata di ordine 3, trovare i valori di
$a$

E

$b$

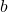
per renderlo ortogonale:

$\displaystyle A=\frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix}$

Affinché l’ortogonalità della matrice sia soddisfatta, il prodotto della matrice per la sua trasposta deve essere uguale alla matrice Identità. COSÌ:

$\displaystyle A\cdot A^t = I$

$\displaystyle \frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix} \cdot \frac{1}{3}\begin{pmatrix}a&b&1\\[1.1ex] a&1&a\\[1.1ex] 1&b&a\end{pmatrix}=\begin{pmatrix}1&0&0\\[1.1ex] 0&1&0\\[1.1ex] 0&0&1\end{pmatrix}$

Moltiplichiamo le matrici:

$\displaystyle \frac{1}{9}\begin{pmatrix}2a^2+1&ab+a+b&2a+a^2\\[1.5ex] ab+a+b&2b^2+1&b+a+ab\\[1.5ex] 2a+a^2&b+a+ab&1+2a^2\end{pmatrix} =\begin{pmatrix}1&0&0\\[1.5ex] 0&1&0\\[1.5ex] 0&0&1\end{pmatrix}$

Ora possiamo ottenere un’equazione dall’angolo in alto a sinistra delle matrici, perché gli elementi in quella posizione devono corrispondere. Ancora:

$\displaystyle \frac{1}{9}(2a^2+1) = 1$

Risolviamo l’equazione ed eliminiamo l’incognita:

$\displaystyle 2a^2+1 = 9$

$\displaystyle 2a^2 = 8$

$\displaystyle a^2 = 4$

$\displaystyle \bm{a = \pm 2}$

Tuttavia, ci sono equazioni che non valgono con la soluzione positiva, ad esempio quella nell’angolo in alto a destra. Quindi è possibile solo la soluzione negativa .

D’altra parte, per calcolare la variabile

$b$

possiamo abbinare, ad esempio, i termini posti nella seconda riga della prima colonna:

$\displaystyle \frac{1}{9}(ab+a+b) = 0$

$\displaystyle ab+a+b = 0$

Sostituendo il valore di

$a$

nell’equazione:

$\displaystyle -2b-2+b = 0$

$\displaystyle -b =2$

$\displaystyle \bm{b =-2}$

In sintesi l’unica soluzione possibile è:

$\displaystyle \bm{a=b =-2}$

Quindi la matrice ortogonale che corrisponde a questi valori è:

$\displaystyle A=\frac{1}{3}\begin{pmatrix}-2&-2&1\\[1.1ex] -2&1&-2\\[1.1ex] 1&-2&-2\end{pmatrix}$

Applicazioni delle matrici ortogonali

Anche se può non sembrare, perché solitamente hanno una forma molto semplice, le matrici ortogonali sono molto importanti in matematica, soprattutto nel campo dell’algebra lineare.

In geometria, le matrici ortogonali rappresentano trasformazioni isometriche (che non modificano distanze e angoli) in spazi vettoriali reali, motivo per cui vengono chiamate trasformazioni ortogonali. Inoltre tali trasformazioni sono isomorfismi interni dello spazio vettoriale considerato. Queste trasformazioni possono essere rotazioni , riflessioni speculari o inversioni .

Infine, questo tipo di matrice viene utilizzata anche in fisica, poiché permette di studiare il movimento dei corpi rigidi. E vengono utilizzati anche nella formulazione di alcune teorie sul campo.