Matrice nilpotente

In questa pagina troverai una spiegazione di cosa sia una matrice nilpotente, oltre a diversi esempi affinché tu possa capirla e non avere dubbi. Inoltre, potrai vedere le strutture delle matrici nilpotenti e tutte le proprietà di questi tipi di matrici.

Cos’è una matrice nilpotente?

La definizione di matrice nilpotente è la seguente:

Una matrice nilpotente è una matrice quadrata che elevata a numero intero dà la matrice zero .

$N^k =0$

Oro

$N$

è la matrice nilpotente e

$k$

l’esponente della potenza che dà la matrice zero.

Questa condizione non significa che la potenza di una matrice nilpotente dà sempre zero indipendentemente dall’esponente, ma piuttosto che se esiste almeno una potenza della matrice il cui risultato è una matrice piena di 0, allora la matrice è nilpotente.

D’altra parte, l’ indice di nilpotenza di una matrice nilpotente è il numero più piccolo con cui è soddisfatta la condizione di nilpotenza. Possiamo anche dire che la matrice nilpotente è di ordine k , dove k è il suo indice di nilpotenza.

Esempi di matrici nilpotenti

Per finire di comprendere il concetto di matrice nilpotente, vedremo diversi esempi di questo tipo di matrice:

Esempio di matrice nilpotente 2 × 2

La seguente matrice quadrata di dimensione 2×2 è nilpotente:

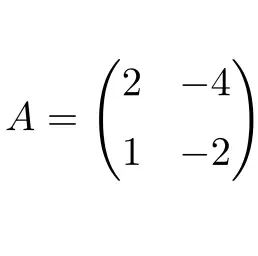
esempio di matrice nilpotente di dimensione 2x2

La matrice è nilpotente perché elevando al quadrato la matrice A si ottiene come risultato la matrice nulla:

$\displaystyle A^2=\begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}\cdot \begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}=\begin{pmatrix} \bm{0} &\bm{0} \\[1.1ex] \bm{0} & \bm{0} \end{pmatrix}$

È quindi una matrice nilpotente e il suo indice di nilpotenza è 2, poiché la matrice zero è ottenuta alla seconda potenza.

Esempio di matrice nilpotente 3×3

La seguente matrice quadrata di ordine 3 è nilpotente:

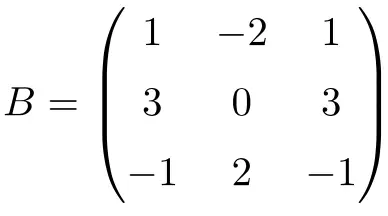
esempio di matrice nilpotente di dimensione 3x3

Sebbene elevando la matrice a 2 non otteniamo la matrice zero:

$\displaystyle B^2=\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}\cdot \begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}$

Ma quando calcoliamo il cubo della matrice, otteniamo una matrice con tutti gli elementi uguali a 0:

$\displaystyle B^3= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}\cdot\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}\bm{0}&\bm{0}&\bm{0}\\[1.1ex]\bm{0}&\bm{0}&\bm{0}\\[1.1ex] \bm{0}&\bm{0}&\bm{0}\end{pmatrix}$

Quindi la matrice B è una matrice nilpotente, e poiché la matrice zero è ottenuta con la potenza di 3, il suo indice di nilpotenza è 3.

Struttura di una matrice 2 × 2 nilpotente

Di seguito puoi vedere la struttura di tutte le matrici nilpotenti. La sua dimostrazione è un po’ noiosa, quindi vi lasciamo direttamente la formula per ottenere una matrice nilpotente di ordine 2:

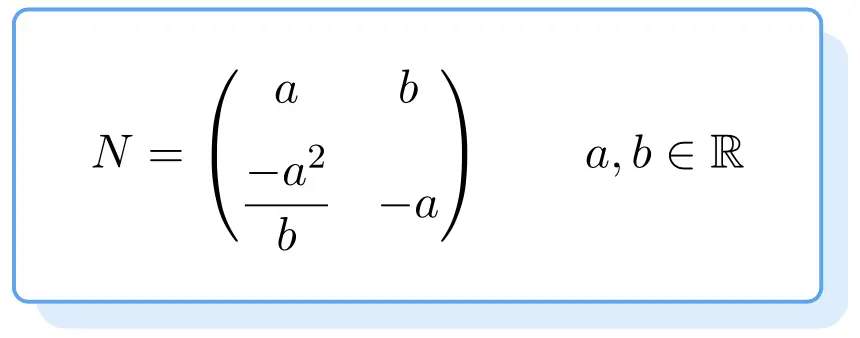
struttura e formula di una matrice 2x2 nilpotente

Quindi qualsiasi matrice che soddisfa la formula di cui sopra sarà una matrice nilpotente. Per questo, i valori

$a$

$b$

possono essere arbitrari purché siano numeri reali.

Proprietà delle matrici nilpotenti

Le matrici nilpotenti hanno le seguenti caratteristiche:

La traccia di una matrice nilpotente è sempre zero.

Allo stesso modo, il determinante di qualsiasi matrice nilpotente è sempre 0. Tuttavia, non è vero il contrario, ovvero il determinante di una matrice è zero non implica che la matrice sia nilpotente.

L’unica matrice nilpotente che può essere diagonalizzata è la matrice zero.

L’indice di nilpotenza di una matrice nilpotente di dimensione n×n è sempre uguale o inferiore a n . Questo è il motivo per cui l’indice di nilpotenza di una matrice nilpotente 2 × 2 sarà sempre 2.

Una matrice nilpotente non è invertibile.

Anche qualsiasi matrice triangolare con zeri sulla diagonale principale è una matrice nilpotente.

C’è un teorema che dice che se la matrice
$N$

è nilpotente, quindi la matrice

$N+I$

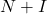
è invertibile, dove

$I$

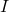
è la matrice identità. Inoltre, la sua matrice inversa può essere trovata con la seguente formula:

$\displaystyle(N+I)^{-1} = \sum_{m = 0}^\infty (-N)^m=I-N+N^2-N^3+\cdots$

Allo stesso modo, se
$N$

è una matrice nilpotente, è possibile calcolare l’inverso della matrice

$N-I$

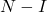
con la seguente equazione:

$\displaystyle(N-I)^{-1} = \sum_{m = 0}^\infty (N)^m=I+N+N^2+N^3+\cdots$

Qualsiasi matrice singolare, cioè non invertibile, può essere scomposta nel prodotto di matrici nilpotenti.

Tutti gli autovalori (o autovalori) di una matrice nilpotente sono zero.

$\displaystyle \lambda=0 \qquad \forall \ \lambda$

Infine, come curiosità, esiste anche il concetto di trasformazione nilpotente, che definisce un’applicazione lineare
$L$

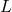
di uno spazio vettoriale tale che

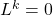
$L^k=0$

.