Linee che si intersecano

In questa pagina troverai tutto sulle linee secanti: cosa significano, i diversi tipi che esistono, come sapere se due linee sono secanti, come trovare il loro punto comune,… Potrai anche vedere diversi esempi ed esercizi risolti di linee secanti.

Cosa sono due linee che si intersecano?

In matematica, la definizione di retta secante è la seguente:

Due linee si intersecano quando si intersecano in un solo punto. Pertanto le rette che si intersecano hanno un solo punto in comune. Inoltre due linee che si intersecano devono necessariamente essere contenute nello stesso piano cartesiano.

Il concetto che due linee che si intersecano in un unico punto è importante perché se avessero più di un punto di intersezione sarebbero linee coincidenti e, invece, se non avessero punti di intersezione, sarebbero linee parallele.

Esempi di linee che si intersecano

Una volta visto il significato di due linee che si intersecano, vediamo ora 2 diversi esempi di questo tipo di linee:

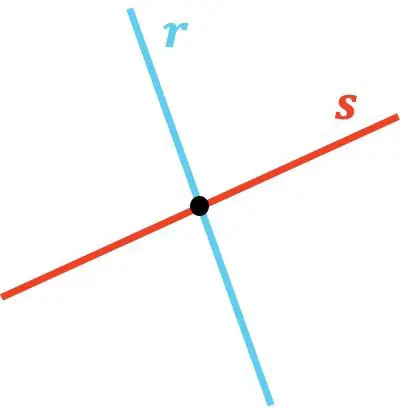
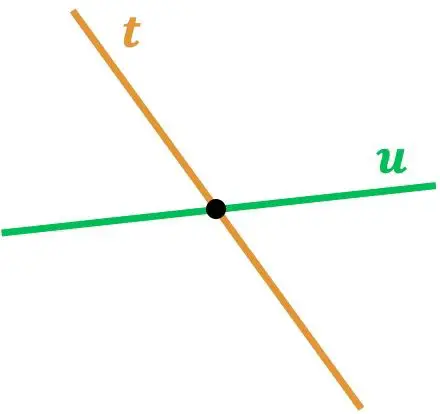
Come puoi vedere, le linee r e s si intersecano perché si toccano in un punto. E, allo stesso modo, la linea t interseca la linea u poiché c’è un punto in cui si intersecano.

Tipi di linee che si intersecano

Esistono due tipi di linee che si intersecano:

Linee perpendicolari : sono linee che si intersecano ad angolo retto di 90º.
Linee oblique: sono costituite da linee che si intersecano con un angolo acuto compreso tra 0º e 90º (non incluso).

Rette perpendicolari

Le linee perpendicolari sono quelle linee che si intersecano per formare quattro angoli di 90 gradi.

Allo stesso modo, le pendenze di due rette perpendicolari soddisfano sempre la seguente condizione:

$m_r = -\cfrac{1}{m_s}$

Un’altra proprietà delle linee perpendicolari che si intersecano è che il prodotto scalare tra i loro vettori di direzione (un vettore che indica la direzione di una linea) è uguale a zero.

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = 0$

Se sei più interessato alle linee perpendicolari, in questo link puoi vedere esempi di linee perpendicolari . Inoltre troverai anche come calcolare una retta perpendicolare ad un’altra, le proprietà di questo tipo di retta, esercizi risolti passo passo, ecc.

linee oblique

Le linee oblique sono quelle linee che si intersecano formando angoli acuti e angoli ottusi a coppie. Vale a dire, formare due angoli acuti (meno di 90º) e due ottusi (maggiori di 90º). Tuttavia, secondo la definizione dell’angolo tra due linee, l’angolo tra due linee è il più piccolo tra quelli che forma.

L’angolo tra due linee oblique con le loro pendenze può essere calcolato utilizzando la seguente formula:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_2-m_1}{1+m_1\cdot m_2} \end{vmatrix}$

Come fai a sapere se due linee si intersecano?

Esistono principalmente 3 metodi per trovare la posizione relativa di due linee:

Con i vettori di direzione delle due rette.
Con le pendenze delle due linee.
Con l’equazione implicita (o generale) delle due rette.

Poi vedremo la spiegazione dei 3 metodi esistenti per sapere quando due linee si intersecano.

Dai vettori di direzione delle linee

Se le coordinate dei vettori di direzione (vettore che segna la direzione di una linea) di due linee diverse non sono proporzionali , queste due linee si intersecano.

Vediamo un esercizio risolto passo passo di due linee che si intersecano:

$\displaystyle r: \ \begin{cases} x=1+2t \\[2ex] y= 5-3t \end{cases}\qquad \qquad s: \ \begin{cases} x=1+t \\[2ex] y=2+4t \end{cases}$

Entrambe le linee sono espresse come equazioni parametriche, quindi i componenti del vettore di direzione di ciascuna linea sono i numeri davanti al parametro

$t:$

$\vv{r} =(2,-3) \qquad \qquad \vv{s}=(1,4)$

Quindi, per vedere se i vettori di direzione sono proporzionali, dobbiamo dividere tra loro le loro coordinate. Se otteniamo lo stesso risultato in entrambe le divisioni, queste saranno proporzionali; se invece il risultato è diverso vorrà dire che i vettori non sono proporzionali.

$\cfrac{2}{1} \neq \cfrac{-3}{4}$

Le divisioni delle componenti non sono equivalenti, quindi i vettori non sono proporzionali e quindi le rette si intersecano.

alla partenza delle piste

Se due rette hanno pendenze diverse ciò implica che le rette si intersecano.

Ad esempio, le seguenti due linee si intersecano perché hanno pendenze diverse:

$r: \ y=-2x+4 \qquad \qquad s: \ y=3x+1$

La pendenza della linea

$r$

è -2 e la pendenza della linea

$s$

è 3.

$m_r =-2 \neq m_s =3$

Poiché le due rette non hanno la stessa pendenza, si intersecano.

Dall’equazione implicita della retta

Si può anche scoprire se due rette si intersecano o meno attraverso le equazioni implicite (o equazioni generali) delle rette. L’equazione implicita della retta è la seguente:

$Ax+By+C=0$

Pertanto, due rette si intersecano quando i loro coefficienti A e B non sono proporzionali.

Vediamo un esempio di due rette che si intersecano definite con la loro equazione implicita:

$r: \ 3x-y+5=0 \qquad \qquad s: \ -2x+6y-1=0$

Per verificare che si tratti di due rette che si intersecano, dobbiamo analizzare la proporzionalità del coefficiente A (numero davanti alla variabile

$x$

) con il coefficiente B (cifra davanti alla variabile

$y$

$\cfrac{3}{-2} \neq \cfrac{-1}{6}$

I due termini non sono proporzionali, quindi effettivamente le due linee si intersecano.

Trova il punto comune di due rette che si intersecano

Come abbiamo visto, le rette che si intersecano hanno un solo punto in comune. Pertanto, per calcolare il punto di intersezione di due rette secanti , è necessario risolvere il sistema di equazioni formato dalle due rette.

Ad esempio, troveremo il punto di intersezione delle seguenti due linee:

$r: \ x+2y-5=0 \qquad \qquad s: \ 2x-3y+3=0$

Per determinare il punto di intersezione delle due rette dobbiamo risolvere il sistema di equazioni lineari formato dalle due rette:

$\left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\}$

In questo caso risolveremo il sistema con il metodo di sostituzione. Isoleremo quindi la variabile

$x$

dalla prima equazione e sostituitela nella seconda equazione:

$\left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\} \begin{array}{l}\longrightarrow \ x=5-2y \\[2ex]&\end{array}$

$2(5-2y)-3y+3=0$

$10-4y-3y=3$

$-4y-3y=3-10$

$-7y=-7$

$y=\cfrac{-7}{-7} = 1$

E una volta che sapremo quanto vale l’ignoto

$y$

Sostituiamo il suo valore nell’espressione trovata per

$x:$

$x=5-2y \ \xrightarrow{y \ = \ 1} \ x=5-2\cdot 1$

$x = 5-2 = 3$

La soluzione del sistema di equazioni è quindi il punto di intersezione delle due rette. E questo punto è

$\bm{(3,1)}.$

linea che interseca un cerchio

Normalmente quando diciamo che due linee si intersecano ci riferiamo al concetto che abbiamo appena visto. Tuttavia, in geometria, esiste un altro significato della linea secante:

Una linea che interseca un cerchio è una linea che interseca un cerchio (o una curva) in due punti diversi.

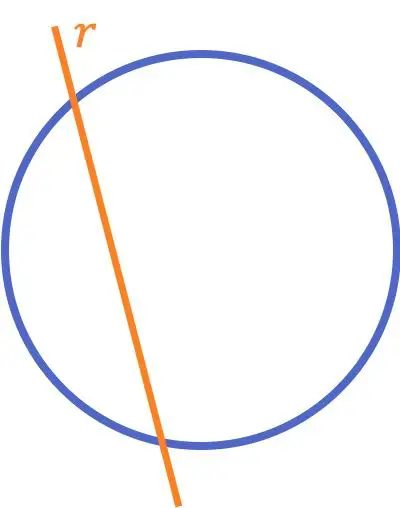
A differenza del concetto di due linee che si intersecano solitamente insegnato alle scuole elementari, questa definizione di linea che si interseca con un cerchio viene spesso studiata nelle classi successive insieme a tutte le posizioni relative delle linee con i cerchi.