In questa pagina troverai la spiegazione della regola (o legge) del parallelogramma. Inoltre, vedrai diversi esempi di addizione e sottrazione di vettori utilizzando la regola del parallelogramma, nonché applicazioni del mondo reale.
Cos’è la regola del parallelogramma?
Come già sai, le quantità vettoriali non possono essere sommate o sottratte allo stesso modo dei numeri reali, perché hanno 2 componenti (in R2) o 3 componenti (in R3) e perché i vettori possono avere direzioni diverse. Pertanto, sono necessari altri metodi per eseguire operazioni sui vettori, come la regola del parallelogramma, che consiste in quanto segue:
In matematica, la regola del parallelogramma è una procedura per aggiungere o sottrarre due vettori dalla loro rappresentazione grafica.
Il metodo del parallelogramma è sicuramente il più utilizzato nell’addizione e sottrazione di vettori (graficamente), perché è una tecnica molto semplice da utilizzare. Ad esempio, in fisica viene utilizzato per aggiungere e sottrarre forze.
D’altra parte, la regola varia leggermente a seconda che vogliamo aggiungere o sottrarre vettori, quindi di seguito spiegheremo entrambe le versioni separatamente.
Regola del parallelogramma per la somma di due vettori
Se vogliamo sommare graficamente due vettori, i passaggi per applicare la regola o legge del parallelogramma sono:
- Per prima cosa disegniamo i vettori e li posizioniamo nello stesso punto di applicazione, cioè poniamo le origini di entrambi i vettori nello stesso punto.
- Quindi disegniamo alla fine di un vettore una linea parallela all’altro vettore. E ripetiamo il passaggio con l’altro vettore. Otterremo quindi il disegno di un parallelogramma (da qui il nome della regola).
- Infine, il vettore risultante dalla somma sarà la diagonale del parallelogramma che va dall’origine comune dei vettori al punto di intersezione delle due rette parallele.
Nel seguente esempio generico puoi vedere come viene utilizzata la regola del parallelogramma:

Se vuoi esercitarti con la regola del parallelogramma, nel link seguente puoi consultare altri esempi e diversi esercizi di addizione di vettori risolti . In questa pagina troverai anche altri metodi per sommare graficamente i vettori e anche come sommarli numericamente.
Regola del parallelogramma per sottrarre due vettori
La regola o metodo del parallelogramma viene utilizzata anche per sottrarre due vettori da un grafico. Quindi, i passaggi per la sottrazione vettoriale sono:
- Per prima cosa rappresentiamo i due vettori sul grafico e li posizioniamo nello stesso punto di applicazione, cioè poniamo le origini di entrambi i vettori nello stesso punto.
- In secondo luogo, disegniamo il vettore opposto a quello che viene sottratto nell’operazione o, in altre parole, invertiamo il vettore che sottrae.
- Quindi disegniamo una linea parallela al vettore di cambio di segno all’estremità del vettore la cui somma dà . E ripetiamo il processo con l’altro vettore. Otterremo così il disegno di un parallelogramma (da cui il nome della regola).
- Infine il risultato della sottrazione sarà il vettore che va dall’origine comune dei due vettori al punto in cui si intersecano le due rette parallele.
Guarda il seguente esempio generico in cui due vettori vengono sottratti dalla legge del parallelogramma:
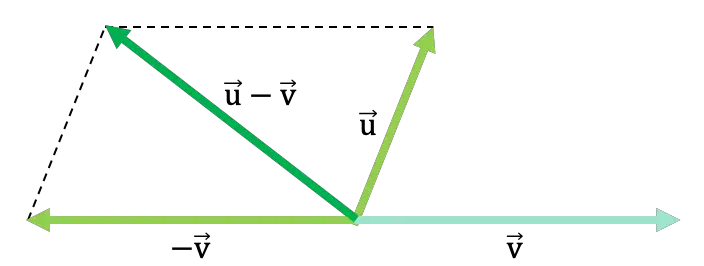
Nel seguente link puoi vedere altri esempi di sottrazione vettoriale con la regola del parallelogramma, puoi anche esercitarti con esercizi di sottrazione vettoriale risolti . Inoltre, troverai altre tecniche per sottrarre i vettori dal loro grafico e, infine, come vengono sottratti numericamente.
Infine, se la spiegazione di questa tecnica ti è stata utile, sicuramente ti interesserà anche sapere qual è la regola della mano destra . Nella pagina dei collegamenti puoi vedere di cosa si tratta, per quale operazione vettoriale viene utilizzato e le diverse varianti di questa regola che esistono.