Combinazione lineare di vettori -

In questa pagina troverai la spiegazione di cosa significa una combinazione lineare tra vettori. Inoltre, potrai vedere un esempio di come si esprime un vettore come combinazione lineare e, inoltre, potrai esercitarti con esercizi e problemi risolti passo dopo passo.

Cos’è la combinazione lineare di vettori?

La definizione di combinazione lineare è la seguente:

Una combinazione lineare di un insieme di vettori è il vettore ottenuto sommando tutti i vettori dell’insieme moltiplicati per scalari (numeri reali).

In altre parole, dato un insieme di vettori

$\vv{\text{v}}_1, \vv{\text{v}}_2,\ldots \vv{\text{v}}_n,$

una loro combinazione lineare sarebbe:

$\vv{\text{w}}=a_1\vv{\text{v}}_1+a_2\vv{\text{v}}_2+\dots + a_n\vv{\text{v}}_n$

Dove i coefficienti

$a_i$

Questi sono numeri reali.

Pertanto, un vettore che è una combinazione lineare di altri vettori significa che il primo può essere espresso in termini del secondo.

Questo concetto può essere meglio compreso rappresentando graficamente un vettore nel piano che è una combinazione lineare di due vettori:

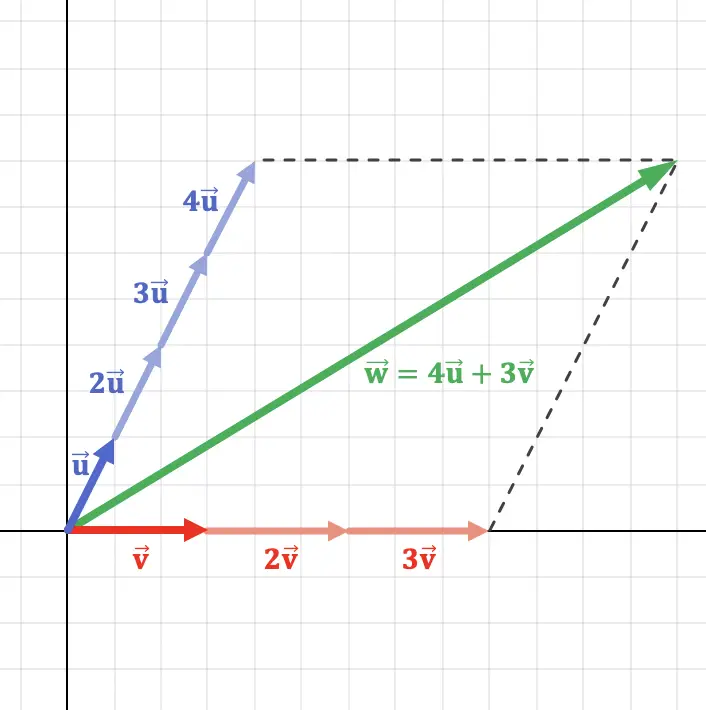
Come puoi vedere nella rappresentazione grafica sopra, il vettore

$\vv{\text{w}}$

possono essere ottenuti da vettori

$\vv{\text{u}}$

$\vv{\text{v}}$

eseguire operazioni sui vettori. Pertanto, il vettore

$\vv{\text{w}}$

è una combinazione lineare degli altri due vettori.

È bene sottolineare che questa combinazione lineare è unica , ovvero esiste una sola combinazione lineare ammissibile per ogni vettore. Poiché, seguendo l’esempio precedente, se moltiplicassimo

$\vv{\text{u}}$

per 6 invece di 4 otterremmo un altro vettore diverso.

Inoltre, una delle proprietà della combinazione lineare nel piano (in R2) è che qualsiasi vettore può essere posto come combinazione lineare di altri due vettori se hanno direzioni diverse, cioè se non sono paralleli.

Inoltre, a volte possiamo identificare a occhio che due vettori sono una combinazione lineare. Per fare ciò è sufficiente che le sue componenti siano proporzionali . Ad esempio, le coordinate dei seguenti due vettori sono proporzionali e, quindi, i vettori sono una combinazione lineare:

$\vv{\text{u}} = (1,2,-1) \qquad \vv{\text{v}} = (3,6,-3)$

$\cfrac{3}{1} = \cfrac{6}{2} = \cfrac{-3}{-1} = 3 \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}$

Infine, sia in uno spazio vettoriale bidimensionale (in R2) che tridimensionale (in R3), se esiste una combinazione lineare all’interno di un insieme di vettori, ciò implica che essi sono linearmente dipendenti l’uno dall’altro. D’altra parte, se non è possibile alcuna combinazione lineare tra i vettori, ciò significa che sono linearmente indipendenti .

Se quest’ultimo concetto non ti è del tutto chiaro, ti consigliamo di consultare la nostra spiegazione dei vettori linearmente dipendenti e indipendenti , qui troverai cosa significa che i vettori sono linearmente dipendenti o indipendenti, esempi di ogni tipo e le differenze tra loro. . Questo concetto è molto usato e, infatti, è chiesto molto agli esami, quindi è importante che tu lo capisca bene.

Come esprimere un vettore come combinazione lineare di altri vettori

Vedremo poi come risolvere un tipico problema in cui ci viene chiesto di trovare la combinazione lineare di un vettore.

Esprimere il vettore
$\vv{\text{x}}$

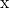
come combinazione lineare di

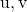
$\vv{\text{u}}, \vv{\text{v}}$

E

$\vv{\text{w}}.$

$\vv{\text{x}} = (3,1,2)$

$\vv{\text{u}} = (1,0,1) \qquad \vv{\text{v}} = (1,2,0) \qquad \vv{\text{w}} = (0,1,-1)$

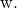
In modo che il vettore

$\vv{\text{x}}$

essere una combinazione lineare degli altri vettori, deve essere soddisfatta la seguente equazione:

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

Dove i coefficienti

$a_1, a_2$

$a_3$

Queste sono le incognite che dobbiamo trovare.

Sostituiamo quindi ogni vettore con le sue coordinate:

$a_1\begin{pmatrix} 1 \\0\\1 \end{pmatrix}+a_2\begin{pmatrix} 1 \\2\\0 \end{pmatrix}+ a_3\begin{pmatrix} 0 \\1\\-1 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

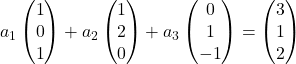
Moltiplichiamo ciascun vettore per il suo coefficiente:

$\begin{pmatrix} a_1 \\0\\a_1 \end{pmatrix}+\begin{pmatrix} a_2 \\2a_2\\0 \end{pmatrix}+ \begin{pmatrix} 0 \\a_3\\-a_3 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

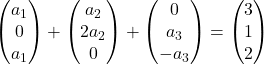
Aggiungiamo i vettori:

$\begin{pmatrix} a_1 +a_2\\2a_2+a_3\\a_1-a_3 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

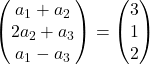
Ciascuna coordinata sinistra deve essere uguale a ciascuna coordinata destra. Abbiamo quindi 3 equazioni:

$\left. \begin{array}{l} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] a_1-a_3 = 2 \end{array} \right\}$

Non resta che risolvere il sistema di equazioni ottenuto. Per fare questo utilizza il metodo che preferisci (metodo di sostituzione, regola di Cramer, metodo di Gauss-Jordan, ecc.), in questo caso utilizzeremo il metodo di Gauss:

$\left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)$

$\left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)\begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2F_3+F_2}\end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&0&-1&-1 \end{array}\right)$

Il sistema di passi ottenuto è quindi:

$\left. \begin{array}{r} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] -a_3 = -1 \end{array} \right\}$

Tutto quello che dobbiamo fare ora è chiarire le incognite e trovarne il valore. Quindi dall’ultima equazione troviamo

$a_3:$

$-a_3 = -1 \ \longrightarrow \ \bm{a_3 = 1}$

Dalla seconda equazione del sistema, calcoliamo il valore di

$a_2:$

$2a_2+a_3 =1 \ \xrightarrow{a_3\ = \ 1} \ 2a_2+1=1$

$2a_2=1-1$

$2a_2=0$

$\bm{a_2=0}$

E infine, dalla prima equazione del sistema di gradini, troviamo l’incognita

$a_1:$

$a_1 +a_2 = 3 \ \xrightarrow{a_3\ = \ 1 \ ; \ a_2 \ = \ 0 } \ \bm{a_1 = 3}$

La soluzione del sistema di equazioni lineari è quindi:

$a_1=3 \qquad a_2=0 \qquad a_3 = 1$

Quindi il vettore

$\vv{\text{x}}$

Può essere espresso dalla seguente combinazione lineare:

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= 3\vv{\text{u}}+0\vv{\text{v}}+ 1\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= 3}\vv{\mathbf{u}} \bm{+} \vv{\mathbf{w}}}$

Esiste quindi effettivamente una dipendenza lineare tra i vettori. D’altra parte, se non fosse stata ottenuta alcuna soluzione del sistema di equazioni, ciò significherebbe che il vettore

$\vv{\text{x}}$

Esso è linearmente indipendente rispetto agli altri vettori e, pertanto, non vi sarebbe alcuna combinazione lineare possibile per ottenere detto vettore dagli altri vettori.

Esercizi risolti sulla combinazione lineare di vettori

Esercizio 1

Tra i seguenti tre vettori, indicare quali coppie sono combinazioni lineari l’una dell’altra. Inoltre, trova la relazione di combinazione lineare di dette coppie di vettori.

$\vv{\text{u}} = (2,4,3) \qquad \vv{\text{v}} = (1,2,-3) \qquad \vv{\text{w}} = (-3,-6,9)$

Vedi la soluzione

Per sapere se una coppia di vettori è una combinazione lineare, dobbiamo vedere se le loro coordinate sono proporzionali.

Per prima cosa controlliamo il vettore

$\vv{\text{u}}$

con il vettore

$\vv{\text{v}} :$

$\cfrac{2}{1} = \cfrac{4}{2} \neq \cfrac{3}{-3} \ \longrightarrow \ \text{No proporcionales}$

In secondo luogo, controlliamo il vettore

$\vv{\text{u}}$

con il vettore

$\vv{\text{w}} :$

$\cfrac{2}{-3} = \cfrac{4}{-6} \neq \cfrac{3}{9} \ \longrightarrow \ \text{No proporcionales}$

Infine, testiamo il vettore

$\vv{\text{v}}$

con il vettore

$\vv{\text{w}} :$

$\cfrac{1}{-3} = \cfrac{2}{-6} = \cfrac{-3}{9} = -\cfrac{1}{3} \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}$

Quindi l’unica coppia di vettori che sono combinazioni lineari lo è

$\vv{\text{v}}$

$\vv{\text{w}}.$

Inoltre il loro rapporto è il seguente:

$\vv{\text{v}}= -\cfrac{1}{3} \vv{\text{w}}$

O equivalente:

$\vv{\text{w}}= -3 \vv{\text{v}}$

Sebbene l’affermazione non lo richieda, gli unici vettori che dipendono linearmente l’uno dall’altro lo sono

$\vv{\text{v}}$

$\vv{\text{w}}$

perché esiste una combinazione lineare tra loro. Le altre coppie sono linearmente indipendenti perché non possono essere combinate linearmente.

Esercizio 2

Trova la relazione lineare tra il vettore

$\vv{\text{x}}$

e l’insieme dei vettori

$\vv{\text{u}}, \vv{\text{v}}$

$\vv{\text{w}}.$

$\vv{\text{x}} = (4,2,5)$

$\vv{\text{u}} = (1,-1,0) \qquad \vv{\text{v}} = (1,2,2) \qquad \vv{\text{w}} = (-1,1,-1)$

Vedi la soluzione

In modo che il vettore

$\vv{\text{x}}$

essere una combinazione lineare degli altri vettori, deve essere soddisfatta la seguente equazione:

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

Sostituiamo quindi ogni vettore con le sue coordinate:

$a_1\begin{pmatrix} 1 \\-1\\0 \end{pmatrix}+a_2\begin{pmatrix} 1 \\2\\2 \end{pmatrix}+ a_3\begin{pmatrix} -1 \\1\\-1 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

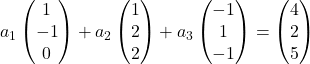
Moltiplichiamo ciascun vettore per la sua costante:

$\begin{pmatrix} a_1 \\-a_1\\0 \end{pmatrix}+\begin{pmatrix} a_2 \\2a_2\\2a_2 \end{pmatrix}+ \begin{pmatrix} -a_3 \\a_3\\-a_3 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

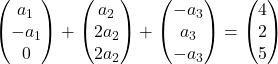
Aggiungiamo i vettori:

$\begin{pmatrix} a_1 +a_2-a_3\\-a_1+2a_2+a_3\\ 2a_2-a_3 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

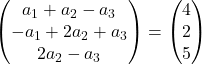
Otteniamo quindi il seguente sistema di equazioni:

$\left. \begin{array}{l} a_1 +a_2-a_3 = 4 \\[2ex] -a_1+2a_2+a_3 =2\\[2ex] 2a_2-a_3 = 5 \end{array} \right\}$

Risolviamo il sistema ottenuto con il metodo di Gauss:

$\left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2+F_1}\\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5\end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3F_3-2F_2} \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&0&-3&3\end{array} \right)$

Il sistema di passi ottenuto è quindi:

$\left. \begin{array}{r} a_1 +a_2-a_3 = 4 \\[2ex] 3a_2 =6\\[2ex] -3a_3 = 3 \end{array} \right\}$

Tutto quello che dobbiamo fare ora è chiarire le incognite e trovarne il valore. Quindi dall’ultima equazione troviamo

$a_3:$

$-3a_3 = 3$

$a_3 = \cfrac{3}{-3} = -1$

Dalla seconda equazione del sistema, calcoliamo il valore di

$a_2:$

$3a_2=6$

$a_2=\cfrac{6}{3} = 2$

E infine, dalla prima equazione del sistema di gradini, troviamo l’incognita

$a_1:$

$a_1 +a_2-a_3 = 4 \ \xrightarrow{a_3\ = \ -1 \ ; \ a_2 \ = \ 2 } \ a_1 +2-(-1) = 4$

$a_1 = 4-2-1$

$a_1 = 1$

La soluzione del sistema di equazioni lineari è quindi:

$a_1=1 \qquad a_2=2 \qquad a_3 = -1$

Quindi il vettore

$\vv{\text{x}}$

Può essere espresso dalla seguente combinazione lineare:

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= 1\vv{\text{u}}+2\vv{\text{v}}-1\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= }\vv{\mathbf{u}}\bm{+} \bm{2} \vv{\mathbf{v}} \bm{-} \vv{\mathbf{w}}$

Esercizio 3

Esprimere il vettore

$\vv{\text{x}}$

come combinazione lineare di vettori

$\vv{\text{u}}, \vv{\text{v}}$

$\vv{\text{w}}.$

$\vv{\text{x}} = (-1,5,-3)$

$\vv{\text{u}} = (1,3,-1) \qquad \vv{\text{v}} = (2,-3,-2) \qquad \vv{\text{w}} = (0,-2,1)$

Vedi la soluzione

Proponiamo l’equazione di combinazione lineare rispetto al vettore

$\vv{\text{x}} :$

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

Sostituiamo quindi ogni vettore con le sue componenti:

$a_1\begin{pmatrix} 1 \\3\\-1 \end{pmatrix}+a_2\begin{pmatrix} 2 \\-3\\-2 \end{pmatrix}+ a_3\begin{pmatrix} 0 \\-2\\1 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

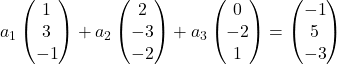
Moltiplichiamo ciascun vettore per la rispettiva incognita:

$\begin{pmatrix} a_1 \\3a_1\\-a_1 \end{pmatrix}+\begin{pmatrix} 2a_2 \\ -3a_2\\ -2a_2 \end{pmatrix}+ \begin{pmatrix} 0 \\-2a_3\\a_3 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

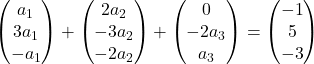
Eseguiamo l’addizione dei vettori:

$\begin{pmatrix} a_1 +2a_2\\3a_1-3a_2-2a_3\\ -a_1-2a_2+a_3 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

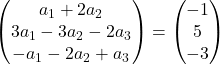
Abbiamo quindi ottenuto il seguente sistema di equazioni:

$\left. \begin{array}{l} a_1 +2a_2 = -1 \\[2ex] 3a_1-3a_2-2a_3 =5\\[2ex] -a_1-2a_2+a_3 = -3 \end{array} \right\}$

Risolviamo il sistema ottenuto con il metodo di Gauss:

$\left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2-3F_1}\\[2ex] \xrightarrow{F_3+F_1} \end{array} \left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 0&-9&-2&8\\[2ex] 0&0&1&-4\end{array} \right)$

Il sistema di passi ottenuto è quindi:

$\left. \begin{array}{r} a_1 +2a_2 = -1 \\[2ex] -9a_2-2a_3 =8\\[2ex] a_3 = -4 \end{array} \right\}$

Tutto quello che dobbiamo fare ora è chiarire le incognite e trovarne il valore. Quindi dall’ultima equazione troviamo

$a_3:$

$a_3 = -4$

Dalla seconda equazione del sistema, troviamo il valore di

$a_2:$

$-9a_2-2a_3 =8 \ \xrightarrow{a_3 \ = \ -4} \ -9a_2-2\cdot (-4) = 8$

$-9a_2+8 = 8$

$-9a_2 = 8-8$

$-9a_2 = 0$

$a_2=\cfrac{0}{-9} = 0$

E infine, dalla prima equazione del sistema di passaggi, risolviamo l’incognita

$a_1:$

$a_1 +2a_2 = -1 \ \xrightarrow{a_2 \ = \ 0 } \ a_1=-1$

La soluzione del sistema di equazioni lineari è quindi:

$a_1=-1 \qquad a_2=0 \qquad a_3 = -4$

Quindi il vettore

$\vv{\text{x}}$

può essere espresso combinando linearmente gli altri vettori:

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= -1\vv{\text{u}}+0\vv{\text{v}}-4\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= -}\vv{\mathbf{u}}\bm{-4} \vv{\mathbf{w}}$

Esercizio 4

Determinare se il vettore

$\vv{\text{x}}$

può essere espresso come una combinazione lineare dei vettori

$\vv{\text{u}}, \vv{\text{v}}$

$\vv{\text{w}}.$

In questo caso, trova l’espressione che li collega.

$\vv{\text{x}} = (2,1,-1)$

$\vv{\text{u}} = (3,-1,1) \qquad \vv{\text{v}} = (-1,2,0) \qquad \vv{\text{w}} = (1,3,1)$

Vedi la soluzione

In modo che il vettore

$\vv{\text{x}}$

essere una combinazione lineare degli altri vettori, deve essere soddisfatta la seguente equazione:

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

Sostituiamo quindi ogni vettore con le sue coordinate:

$a_1\begin{pmatrix} 3 \\-1\\1 \end{pmatrix}+a_2\begin{pmatrix} -1 \\2\\0 \end{pmatrix}+ a_3\begin{pmatrix} 1 \\3\\1 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

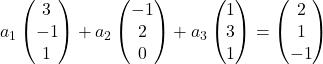
Moltiplichiamo ciascun vettore per il suo coefficiente:

$\begin{pmatrix} 3a_1 \\-a_1\\a_1 \end{pmatrix}+\begin{pmatrix} -a_2 \\2a_2\\0 \end{pmatrix}+ \begin{pmatrix} a_3 \\3a_3\\a_3 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

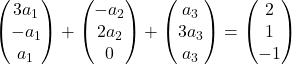
Aggiungiamo i vettori:

$\begin{pmatrix} 3a_1 -a_2+a_3\\-a_1+2a_2+3a_3\\ a_1+a_3 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

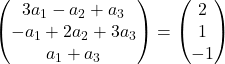
L’espressione precedente equivale quindi al seguente sistema di equazioni:

$\left. \begin{array}{l} 3a_1 -a_2+a_3 = 2 \\[2ex] -a_1+2a_2+3a_3 =1\\[2ex] a_1+a_3 = -1 \end{array} \right\}$

Risolviamo ora il sistema ottenuto con il metodo di Gauss:

$\left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right)$

$\left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{3F_2+F_1}\\[2ex] \xrightarrow{3F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5\end{array} \right)$

$\left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5F_3-F_2} \end{array} \left( \begin{array}{ccc|c}3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&0&0&-30\end{array} \right)$

Abbiamo quindi ottenuto il seguente sistema di equazioni:

$\left. \begin{array}{r} 3a_1 -a_2+a_3 = 2 \\[2ex] 5a_2 +10a_3=5\\[2ex] 0 = -30 \end{array} \right\}$

Tuttavia, l’ultima equazione non potrà mai essere soddisfatta, poiché 0 non sarà mai uguale a -30 qualunque siano i valori assunti dalle incognite. Pertanto il sistema non ha soluzione e questo implica che non esiste alcuna combinazione lineare per calcolare il vettore

$\vv{\text{x}}.$

Cos’è la combinazione lineare di vettori?

Come esprimere un vettore come combinazione lineare di altri vettori

Esercizi risolti sulla combinazione lineare di vettori

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Lascia un commento Annulla risposta