Un’equazione quadratica o equazione quadratica è un’equazione di grado 2, con la quale il massimo esponente di uno dei suoi termini è uguale a 2. Ciò significa che l’equazione può avere fino a due soluzioni diverse, sebbene possa anche avere un’unica soluzione o proprio nessuno.
Per calcolare le soluzioni o radici delle equazioni quadratiche possiamo seguire due diversi procedimenti: mediante la formula quadratica oppure fattorizzando l’espressione . In questo articolo parleremo di entrambi i metodi e vi forniremo alcuni esercizi pratici. Anche se prima chiariremo alcuni concetti in modo che l’intera spiegazione sia ben compresa e tu possa ottenere il massimo dalla lettura.
Tipi di equazioni quadratiche
La principale categorizzazione tra equazioni quadratiche si basa sulla struttura dell’espressione stessa. Pertanto, la struttura standard o usuale di queste espressioni è la seguente: ax² + bx + c . Questa forma comune equivale a un’equazione completa, ma quando sono presenti termini nulli o nulli, la struttura può variare, ed è qui che compaiono equazioni incomplete. Successivamente, spiegheremo le caratteristiche di tutti i tipi in modo più dettagliato.
Equazioni quadratiche complete
Come abbiamo già detto, abbiamo le equazioni quadratiche complete , queste hanno tutti i coefficienti a, b e c diversi da zero. L’espressione segue quindi alla lettera la struttura ax² + bx + c, poiché presenta tutti i termini: il termine quadratico, il termine lineare e il termine indipendente. Un esempio di questo tipo è la seguente equazione: x² + 2x + 1 = 0.
Equazioni quadratiche incomplete
Per quanto riguarda le equazioni incomplete, possiamo distinguerle a seconda di quale coefficiente è uguale a zero. Ricorda che se questa spiegazione non risolve i tuoi dubbi, subito sotto c’è un’immagine in cui puoi trovare tutti i casi spiegati passo passo.
- Equazioni incomplete (b = 0): in questa prima situazione troviamo un’espressione che segue la seguente struttura: ax² + c = 0. Con la quale otteniamo due risultati: il negativo e il positivo della radice della frazione c/a .
- Equazioni incomplete (c = 0): quando abbiamo la forma ax² + bx = 0 dobbiamo fattorizzare l’equazione per avere l’espressione x (ax + b) = 0. Avremo quindi due soluzioni: x = 0 e x = – b/a.
- Equazioni incomplete (b = c = 0): in questo caso abbiamo un’equazione ax² = 0 e abbiamo una sola soluzione possibile, che è x = 0.
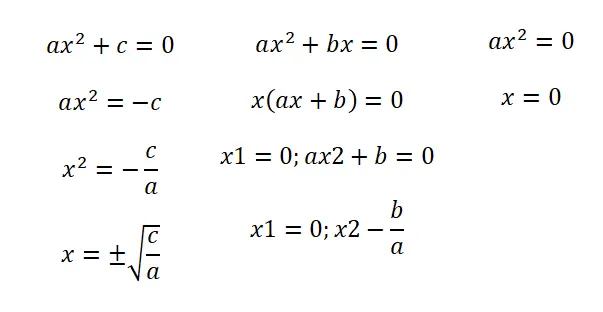
Vale la pena ricordare che le procedure che ti abbiamo insegnato ti consentono di andare più velocemente quando risolvi equazioni incomplete. Ma in ogni caso puoi usare la formula quadratica che ti insegneremo di seguito, dovrai solo scrivere uno zero nei coefficienti che non esistono.
Formula per equazioni quadratiche
Per risolvere le equazioni quadratiche (ax² + bx + c = 0), dobbiamo applicare la formula generale o formula quadratica e quindi sostituire i valori numerici che corrispondono a ciascuna lettera nell’espressione matematica.
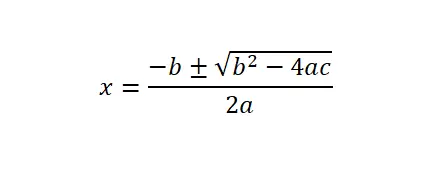
Inoltre, è importante spiegare che il discriminante (Δ) è l’espressione b² – 4ac, che si trova sotto la radice quadrata. Da questo concetto matematico possiamo sapere quante soluzioni ha questa equazione quadratica. Fondamentalmente ci sono tre opzioni: il discriminante è negativo (non ci sono soluzioni reali), il discriminante è zero (c’è una sola soluzione) o il discriminante è positivo (ci sono due soluzioni).
Esempio di un’equazione quadratica completa risolta
Prova a risolvere la seguente equazione quadratica: 2x²+4x-6=0 e controlla il tuo risultato con quello qui sotto. Ti consigliamo di seguire la seguente procedura: analizzare il tipo di equazione (individuare i termini zero), calcolare il discriminante per conoscere il numero di soluzioni esistenti e infine risolvere con la formula l’equazione proposta.
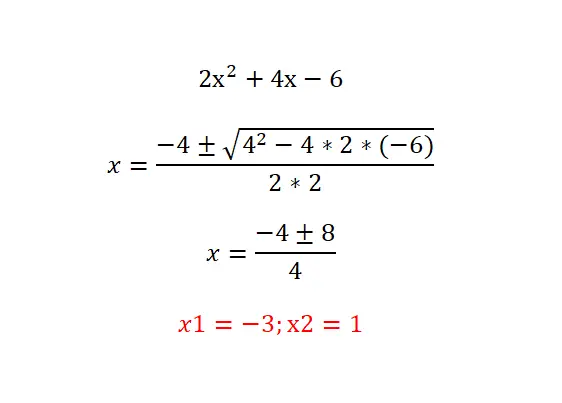
Equazioni quadratiche fattoriali
Il secondo metodo che abbiamo per risolvere le equazioni quadratiche è la fattorizzazione . Quindi, per fattorizzare un polinomio (nel nostro caso un polinomio quadratico), possiamo utilizzare diversi metodi. Sebbene in generale, quando si tratta di equazioni di questo stile, di solito sono fattorizzabili con un termine comune. In caso contrario, puoi provare ad applicare Identità notevoli , ma normalmente non avrai bisogno di conoscere altri metodi in queste situazioni.
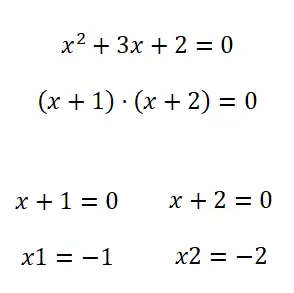
Esercizi sulle equazioni quadratiche con soluzioni
Di seguito troverai una serie di esercizi sulle equazioni quadratiche complete e incomplete . In questo modo ripasserai tutta la teoria spiegata in questo articolo e ti sarà più chiaro come applicarla negli esercizi. Ti consigliamo di provare a risolverli da solo e di guardare la soluzione solo quando li hai completati o quando rimani bloccato. Detto questo, puoi iniziare a risolvere gli esercizi adesso.
Esercizio 1
Risolvi la seguente equazione quadratica:
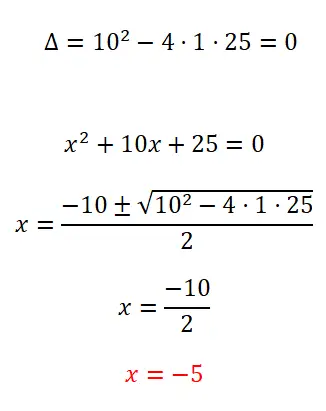
- Iniziamo calcolando il discriminante, per conoscere il numero di soluzioni possibili.
- Poiché si tratta di un’equazione quadratica completa, applichiamo la formula quadratica e risolviamo i calcoli.
- Otteniamo il valore dell’incognita x.
Esercizio 2
Risolvi la seguente equazione quadratica:
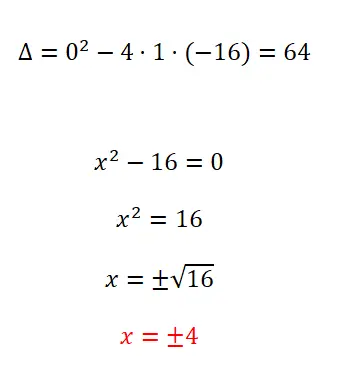
- Iniziamo calcolando il discriminante.
- Poiché abbiamo un’equazione quadratica incompleta in cui b = 0, applichiamo lo standard per equazioni di questo tipo.
- Risolviamo il calcolo per ottenere il risultato e non possiamo dimenticare il segno ±.
Esercizio 3
Risolvi la seguente equazione quadratica non ordinata:
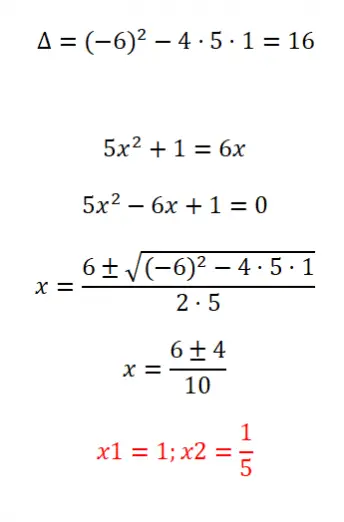
- Iniziamo calcolando il discriminante dell’equazione.
- Prima di poter applicare la formula, dobbiamo ordinare l’equazione secondo la struttura ax² + bx + c = 0.
- Quindi applichiamo la formula generale.
- E finalmente otteniamo i risultati.
Esercizio 4
Risolvi la seguente equazione quadratica fattorizzando:
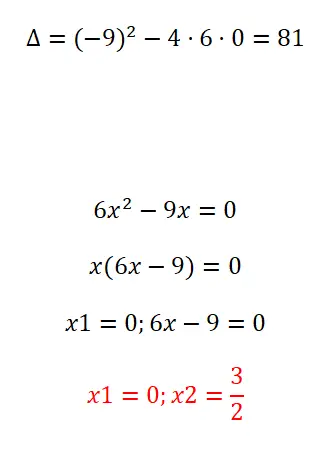
- Per prima cosa calcoliamo il discriminante.
- Successivamente, estraiamo il fattore comune di x.
- Quindi la prima soluzione è x = 0.
- E il secondo è x = 3/2.
Esercizio 5
Risolvi l’equazione quadratica completa che mostriamo di seguito:
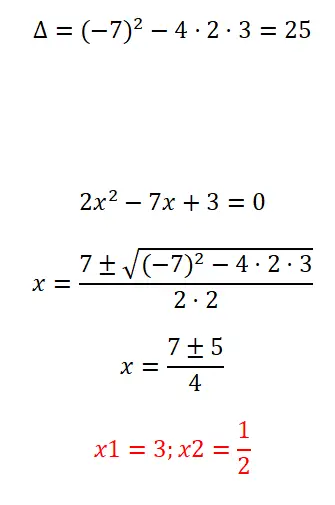
- Come sempre calcoliamo il discriminante per scoprire quante soluzioni ha l’equazione in questione.
- Successivamente, applichiamo la formula quadratica, poiché è un’equazione completa.
- Infine, esprimiamo il risultato dell’equazione.
Esercizio 6
Risolvi l’equazione quadratica con le frazioni che offriamo:
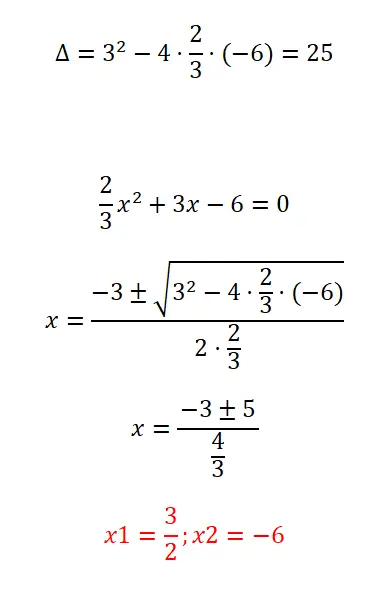
- Iniziamo calcolando il discriminante dell’espressione.
- Successivamente applichiamo la formula quadratica, tenendo conto che il coefficiente “a” è formato da una frazione.
- Risolviamo il calcolo.
- E abbiamo già le due radici dell’equazione.
Esercizio 7
Risolvi la seguente equazione quadratica:
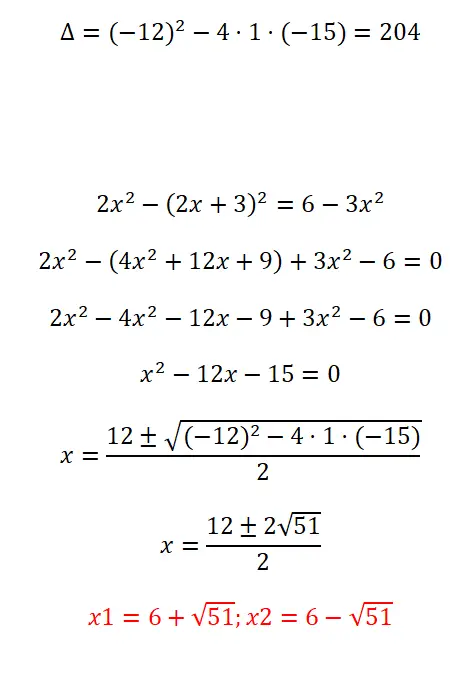
- Iniziamo calcolando il discriminante.
- Prima di applicare la formula dobbiamo semplificare l’espressione e darle la forma ax² + b + c = 0.
- Sostituiamo tutti i coefficienti nella formula e risolviamo il calcolo.
- Finalmente otteniamo il risultato.
Esercizio 8
Prova di risoluzione della seguente equazione quadratica:
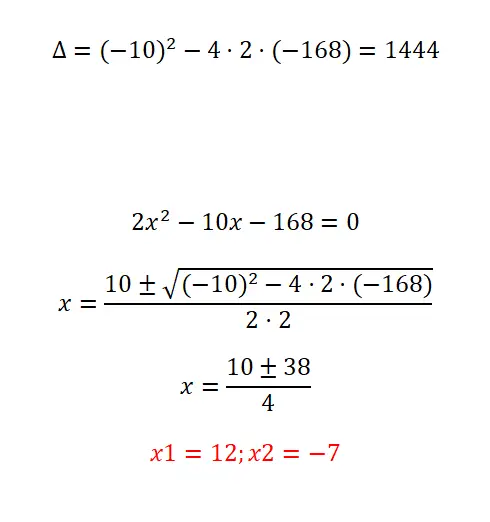
- Iniziamo calcolando il discriminante.
- Come puoi vedere, questa è una semplice equazione quadratica, sebbene abbia coefficienti piuttosto grandi. Dobbiamo quindi applicare la formula e fare attenzione quando eseguiamo le operazioni.
- Alla fine otteniamo entrambe le possibili soluzioni.