In questa pagina troverai le formule per tutte le equazioni del piano e come vengono calcolate. Scoprirai anche come trovare l’equazione di qualsiasi piano con il suo vettore normale. Inoltre, potrai vedere esempi ed esercitarti con esercizi risolti delle equazioni del piano.
Qual è l’equazione del piano?
Nella geometria analitica, l’ equazione di un piano è un’equazione che consente di esprimere matematicamente qualsiasi piano. Quindi, per trovare l’equazione di un piano, hai solo bisogno di un punto e di due vettori linearmente indipendenti appartenenti a quel piano.
Prima di continuare con la spiegazione delle equazioni del piano, è essenziale che tu capisca cos’è il piano (geometria) , perché altrimenti ci saranno cose che non capirai. Se non ti è del tutto chiaro, puoi verificarlo a questo link, dove abbiamo concentrato tutto ciò che devi sapere sul piano.
Quali sono le equazioni del piano?
Come abbiamo visto nella definizione dell’equazione del piano, qualsiasi punto su un piano piano può essere espresso come una combinazione lineare di 1 punto e 2 vettori.

Tuttavia, condizione necessaria affinché l’equazione corrisponda ad un piano è che i due vettori del piano siano indipendenti linearmente, cioè i due vettori non possano essere paralleli tra loro.
Pertanto, tutti i tipi di equazioni del piano sono: l’ equazione vettoriale , le equazioni parametriche , l’ equazione implicita (o generale) e l’ equazione canonica (o segmentale) del piano.
Poi vedremo nel dettaglio la spiegazione e la formula di tutte le equazioni del piano.
Equazione vettoriale del piano
Consideriamo un punto e due vettori di direzione di un piano:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
La formula per l’equazione vettoriale di un piano è:
![]()
O equivalente:
![]()
Oro
![]()
E
![]()
sono due scalari, cioè due numeri reali.
Equazioni parametriche del piano
L’equazione parametrica di un piano può essere determinata dalla sua equazione vettoriale. Qui sotto potete vedere la demo.
Sia l’equazione vettoriale di qualsiasi piano:
![]()
Operiamo e realizziamo prima i prodotti dei vettori per gli scalari:
![]()
Successivamente, aggiungiamo i componenti:
![]()
E, infine, otteniamo le equazioni parametriche del piano assimilando separatamente le coordinate corrispondenti a ciascuna variabile:
![]()
Oro:
-
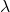
E
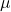
sono due scalari, cioè due numeri reali.
-
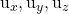
sono le componenti di uno dei due vettori guida del piano
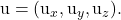
-
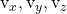
sono le componenti dell’altro vettore direttivo del piano
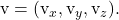
Equazione implicita o generale del piano
Consideriamo un punto e due vettori di direzione di un piano:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
L’equazione implicita, generale o cartesiana di un piano si ottiene risolvendo il seguente determinante e ponendo il risultato uguale a 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
Pertanto, l’ equazione implicita o generale del piano risultante sarà la seguente:
![]()
Questo tipo di equazione piana è anche chiamata equazione piana cartesiana.
Equazione canonica o segmentale del piano
La formula per l’equazione canonica o segmentale di un piano è la seguente:
![]()
Oro:
-

è il punto di intersezione tra il piano e l’asse X.
-

è il punto di intersezione tra il piano e l’asse Y.
-

Qui è dove il piano interseca l’asse Z.
L’equazione canonica (o segmentale) del piano si può ricavare anche dalla sua equazione generale:
![]()
Innanzitutto, risolviamo il coefficiente D dall’equazione:
![]()
Quindi dividiamo l’intera equazione del piano per il valore del parametro D cambiato segno:
![]()
![]()
E, utilizzando le proprietà delle frazioni, arriviamo alla seguente espressione:
![]()
Da questa espressione deduciamo quindi le formule che permettono di calcolare direttamente i termini dell’equazione canonica o segmentale di un piano:
![]()
di conseguenza, per poter formare questa variante delle equazioni del piano, i coefficienti A, B e C devono essere diversi da zero, evitando così indeterminazioni delle frazioni.
Come calcolare l’equazione di un piano dal suo vettore normale
Un problema molto tipico nelle equazioni di un piano è trovare come appare l’equazione di un dato piano dato un punto e il suo vettore normale (o perpendicolare). Quindi, vediamo come funziona.
Ma devi prima sapere che le componenti X, Y, Z del vettore normale ad un piano coincidono rispettivamente con i coefficienti A, B, C dell’equazione implicita (o generale) di detto piano.
![]()
Oro
![]()
è il vettore ortogonale al piano
![]()
Una volta conosciuta la relazione precedente, vediamo un esempio di risoluzione di questo tipo di problemi di equazioni piane:
- Determina l’equazione implicita o generale del piano che passa per il punto
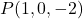
e uno dei suoi vettori normali lo è
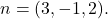
La formula per l’equazione implicita, generale o cartesiana di un piano è:
![]()
Quindi dal vettore normale possiamo ricavare i coefficienti A, B e C perché sono equivalenti alle componenti del suo vettore normale:
![]()
Mentre dobbiamo solo trovare il parametro D. Per fare ciò, sostituiamo nell’equazione le coordinate del punto che appartiene al piano:
![]()
![]()
![]()
![]()
![]()
Quindi l’equazione implicita o generale del piano è:
![]()
Problemi di equazioni del piano risolti
Esercizio 1
Determinare l’equazione vettoriale del piano che contiene il vettore
![]()
e passa attraverso i seguenti due punti:
![]()
E
![]()
Per conoscere l’equazione di un piano occorrono un punto e due vettori e in questo caso abbiamo un solo vettore, dobbiamo quindi trovare un altro vettore direttore del piano. Per fare ciò possiamo calcolare il vettore che definisce i due punti del piano:
![]()
Ora che conosciamo già due vettori di direzione del piano e un punto, utilizziamo quindi la formula per l’equazione vettoriale del piano:
![]()
E sostituiamo nell’equazione i due vettori e uno dei due punti del piano:
![]()
Esercizio 2
Trova le equazioni parametriche del piano che contiene i seguenti tre punti:
![]()
Per trovare le equazioni parametriche del piano, dobbiamo trovare due vettori linearmente indipendenti che si collegano nel piano. E, per questo, possiamo calcolare due vettori definiti dai 3 punti:
![]()
![]()
Le coordinate dei due vettori trovati non sono proporzionali, quindi sono linearmente indipendenti tra loro.
Ora che conosciamo già due vettori di direzione e un punto sul piano, applichiamo la formula per l’equazione parametrica del piano:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5adabb85c9285653d6b638f7c48ba50_l3.png)
E sostituiamo nell’equazione i due vettori e uno dei tre punti del piano:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=4 + \lambda \cdot (-2)+ \mu \cdot (-3) \\[1.7ex] y=1 + \lambda \cdot (-4) + \mu \cdot 4 \\[1.7ex] z=0 + \lambda\cdot (-1) + \mu \cdot 3 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f57edaf8a85108cffb796470ffca8484_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=4 -2 \lambda-3\mu } \\[1.7ex] \bm{y=1-4 \lambda+4 \mu } \\[1.7ex] \bm{z=-\lambda + 3\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4cab5ddc074bd7df6849d71854207cf5_l3.png)
Esercizio 3
Trova l’equazione implicita o generale del piano che passa per il punto
![]()
e contiene i vettori
![]()
E
![]()
Per calcolare l’equazione generale o implicita del piano è necessario risolvere il seguente determinante formato dai due vettori, dalle tre variabili e dalle coordinate del punto:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-917f1770ff2a17897e5df76998ec3519_l3.png)
Quindi sostituiamo i vettori e il punto nella formula:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-02e103601cd9992a8a8c087d016a08c1_l3.png)
E ora risolviamo il determinante della matrice 3×3 con il metodo che preferisci:
![]()
Infine, eseguiamo le operazioni e raggruppiamo termini simili:
![]()
![]()
![]()
Quindi l’equazione implicita o generale del piano è:
![]()
Esercizio 4
Determinare se il punto
![]()
appartiene al seguente piano:
![]()
Affinché il punto sia nel piano, è necessario verificarne l’equazione. Dobbiamo quindi sostituire le coordinate cartesiane del punto nell’equazione del piano e verificare se l’equazione è soddisfatta:
![]()
![]()
![]()
![]()
![]()
Il punto non rispetta l’equazione del piano, quindi non fa parte di questo piano.
Esercizio 5
Trova l’equazione segmentale del piano la cui equazione generale (o implicita) è:
![]()
Innanzitutto, eliminiamo il termine indipendente dall’equazione:
![]()
Quindi dividiamo l’intera equazione del piano per il valore del coefficiente D cambiato segno:
![]()
![]()
E, utilizzando le proprietà delle frazioni, arriviamo alla seguente espressione:
![]()
Quindi l’equazione segmentale (o canonica) del piano è:
![]()
Esercizio 6
Calcola l’equazione implicita o generale del piano nello spazio che passa per il punto
![]()
e uno dei suoi vettori normali lo è
![]()
La formula per l’equazione implicita, generale o cartesiana di un piano è:
![]()
Ebbene, dal vettore normale possiamo ricavare i coefficienti A, B e C, perché sono rispettivamente uguali alle componenti del vettore normale:
![]()
Quindi dobbiamo solo trovare il parametro D. Per fare ciò, sostituiamo nell’equazione le coordinate del punto che appartiene al piano:
![]()
![]()
![]()
![]()
![]()
In conclusione l’equazione implicita o generale del piano è:
![]()
Esercizio 7
Trova le equazioni parametriche del piano che contiene la retta
![]()
ed è parallelo a destra
![]()
essendo le linee:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=1+t \\[1.7ex] y=2-3t\\[1.7ex] z=4+2t \end{cases} \qquad \qquad s: \ \frac{x-4}{2} = \frac{y+3}{2}= \frac{z-2}{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-624f315685b292c4bb05e9cb4b931a97_l3.png)
Per trovare le equazioni parametriche del piano, dobbiamo conoscere due vettori di direzione e un punto sul piano. La dichiarazione ci dice che contiene la riga
![]()
Pertanto, possiamo prendere il vettore direzione e un punto su questa linea per definire il piano. Inoltre l’affermazione ci dice che il piano è parallelo alla retta
![]()
quindi possiamo anche usare il vettore direzione di questa linea per l’equazione del piano.
la destra
![]()
è espresso sotto forma di equazioni parametriche, quindi le componenti del suo vettore direzione sono i coefficienti dei termini del parametro
![]()
![]()
E le coordinate cartesiane di un punto su questa stessa linea sono i termini indipendenti delle equazioni parametriche:
![]()
D’altra parte, la linea retta
![]()
ha la forma di un’equazione continua, tale che le componenti del suo vettore di direzione sono i denominatori delle frazioni:
![]()
Pertanto le equazioni parametriche del piano sono:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5adabb85c9285653d6b638f7c48ba50_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=1 + \lambda \cdot 1+ \mu \cdot 2 \\[1.7ex] y=2 + \lambda \cdot (-3) + \mu \cdot 2 \\[1.7ex] z=4 + \lambda\cdot 2 + \mu \cdot (-3) \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c81f4d8e5aa907f111b3389d5137736e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=1 + \lambda+2\mu } \\[1.7ex] \bm{y=2-3 \lambda+2 \mu } \\[1.7ex] \bm{z=4+2\lambda -3\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fccd86ac9a3e4084e324d8e5b1071e59_l3.png)