Le equazioni di primo grado o equazioni lineari sono la base dell’algebra , perché se non le capisci, ti sarà molto difficile comprendere equazioni più complesse. Quindi la particolarità di questo tipo di equazioni è che la parte letterale dei monomi non può avere esponente. Pertanto in un’equazione lineare troveremo solo monomi senza parte letterale e monomi con parte letterale senza esponente, come ad esempio: 3 + x = -5 – 3x .
Tieni inoltre presente che queste equazioni di solito hanno una soluzione unica, anche se potrebbero non averla. Per sapere quale caso abbiamo di fronte, dobbiamo risolvere l’equazione e alla fine analizzare il risultato . Quindi, se otteniamo un’uguaglianza impossibile come 2 = 0, l’equazione non ha soluzione. Se invece otteniamo un’uguaglianza sempre vera, allora la soluzione è equivalente a tutti i numeri reali. E infine, se alla fine otteniamo l’uguaglianza di X e un valore numerico, in questo caso avremo un risultato unico.
Procedura per risolvere un’equazione lineare
Risolvere un’equazione equivale a calcolare il valore di una variabile, rappresentata da una lettera (x, y, a, b…). Quindi, per trovare questo valore dobbiamo seguire i seguenti passaggi:
- Risolvi parentesi e frazioni: per iniziare, rimuoviamo tutte le parentesi e i denominatori, in modo da ottenere un’equazione più facile da capire. Poiché possiamo apprezzare direttamente quali termini sono accompagnati dall’ignoto e quali no, questa lettura ci permette di continuare facilmente a risolvere l’espressione.
- Semplifichiamo l’espressione: raggruppiamo termini simili (termini indipendenti da un lato, termini con x dall’altro). Quindi lasceremo da una parte i numeri che hanno l’incognita e passeremo gli altri numeri dalla parte opposta. Ma ricorda, per cambiare lato dobbiamo cambiare segno.
- Operare su ciascun lato: Eseguiamo tutte le operazioni nel seguente ordine: potenze/radici, moltiplicazioni/divisioni e addizioni/sottrazioni. Lo facciamo finché non otteniamo un singolo termine su ciascun membro, e così otteniamo un’equazione con la stessa struttura di questa: 4x = 8.
- Isolamo la variabile: infine, basta passare il valore che accompagna la lettera dividendo dall’altra parte e troviamo così il suo valore finale. Alla fine di questo passaggio avremo risolto l’incognita e sapremo che tipo di risultato rimane: una soluzione unica, una soluzione non valida o una soluzione che soddisfa tutti i numeri interi.
Esempi di equazioni di primo grado
Di seguito troverai le equazioni di primo grado risolte , che sono organizzate in diverse categorie a seconda della complessità della loro struttura. Quindi, conoscendo la procedura teorica per risolvere le equazioni lineari e le diverse tipologie esistenti, avrai già le conoscenze necessarie per poterle risolvere facilmente e inizieremo con la pratica. Detto questo cominciamo con la spiegazione teorica:
Equazioni fondamentali di primo grado
Questo primo tipo di equazioni lineari consiste solo di operazioni aritmetiche di base (addizione, sottrazione, moltiplicazione e divisione). Ecco due esempi concreti, il primo è un po’ più basilare e il secondo è un po’ più complesso in termini di calcolo:
-6x + 4 – 1 = 6x -3
-6x + 3 = 6x – 3
-6x – 6x = -3 – 3
-12x = -6
x = 1 /2
-24x – 3 + 4x = -4x – 27
-20x – 3 = -4x – 27
-20x + 4x = -27 + 3
-16x = -24
x = 3/2
Equazioni di primo grado con parentesi
In secondo luogo, abbiamo le equazioni lineari tra parentesi. Queste sono un po’ più complicate da risolvere delle precedenti, anche se la loro unica difficoltà risiede nel calcolo, poiché le proprietà delle parentesi devono essere rispettate. Per renderlo più chiaro, vi mostriamo due esempi realizzati:
2(x + 3) – 4x = -4
2x + 6 – 4x = -4
-2x = -10
x = 5
-2 + 3 (4x + 5) = -1 (x + 2) + 2 (-3x + 2)
-2 + 12x + 15 = -x – 2 – 6x + 4
13 + 12x = -7x + 2
12x + 7x = -13 + 2
19x = -11
x = -11/19
Equazioni di primo grado con potenze e radici
Il terzo livello è abbastanza semplice, poiché aggiunge solo poteri e radici. L’unica difficoltà che potresti incontrare con queste equazioni è quando l’esponente o la radice influisce su una parentesi intera (come nel secondo esempio che ti mostreremo), ma tutto il resto rimane praticamente lo stesso. Di seguito sono riportati due esempi.
3² + √25 – 2x = 2³x + 4
9 + 5 – 2x = 8x + 4
14 – 2x = 8x + 4
-2x – 8x = -14 + 4
-10x = -10
x = 1
4x + (2 – 1 +5)² = 3x – √16
4x + 6² = 3x – 4
4x – 3x = -4 -36
x = -40
Equazioni di primo grado con frazioni
L’ultima categoria di equazioni lineari che possiamo trovare è questa, che è composta da tutti gli elementi che abbiamo commentato in precedenza e anche da frazioni. Questo livello è il più complesso ed esistono diversi metodi per risolverli. Il primo e più semplice è moltiplicare i denominatori per il lato opposto dell’uguaglianza, anche se possiamo usarlo solo quando abbiamo due frazioni. D’altra parte, se abbiamo più di due frazioni nell’equazione, dobbiamo trovare un denominatore comune e moltiplicare tutte le frazioni dividendo quel valore per il denominatore della stessa frazione. Di seguito è riportato un esempio di ciascun tipo:
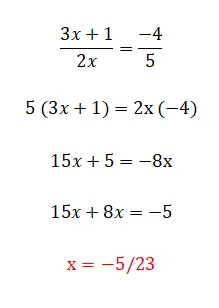
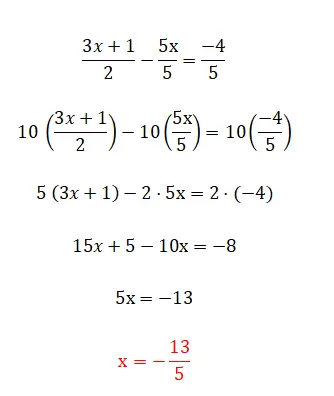
Esercizi sulle equazioni di primo grado
Ora offriamo alcuni esercizi di equazioni lineari. Sono organizzati in base alla difficoltà crescente, con le prime equazioni più facili delle ultime. Pertanto, ti consigliamo di iniziare dall’inizio e vedere fino a che punto puoi arrivare. Quindi, prova a risolvere le seguenti equazioni e poi confronta il tuo risultato con le soluzioni che forniamo.
Primo esercizio
Il primo esercizio è un’equazione lineare molto semplice, poiché consiste solo di addizioni e sottrazioni, e inoltre ha solo quattro termini tra i due membri dell’uguaglianza:
2x – 3 = 4x + 5
2x – 4x = 5 + 3
-2x = 8
x = 8 / (-2)
x = -4
- Raggruppiamo insieme termini simili.
- Semplifichiamo entrambi i lati.
- Cancelliamo l’ignoto e ne calcoliamo il valore.
secondo esercizio
In questo caso ci troviamo con un’equazione formata da parentesi, con la quale la nostra priorità assoluta è eliminarle, in modo da poter poi raggruppare insieme termini simili:
-4(x + 2) + 5x = 6 + 5x
-4x – 8 + 5x = 6 + 5x
-4x + 5x – 5x = 6 + 8
-4x = 14
x = 14/(-4) = -7/2
- Risolviamo le parentesi.
- Spostiamo le x a sinistra e i termini indipendenti a destra.
- Chiariamo l’ignoto.
Semplifichiamo il risultato.
terzo esercizio
Successivamente, dovrai risolvere un’altra equazione quadratica con parentesi, anche se questa è un po’ più difficile. Questo perché ha parentesi annidate (parentesi all’interno di altre parentesi). Occorre quindi seguire correttamente l’ordine di risoluzione: prima gli insider poi gli outsider.
3x + 2 (x – (4x – 5)) = 1 – (3 (2x + 7) – 2)
3x + 2 (x – 4x + 5) = 1 – (6x + 21 – 2)
3x + 2x – 8x + 10 = 1 – 6x – 21 + 2
-3x + 10 = -6x – 18
3x = -28
x = -28/3
- Iniziamo risolvendo le parentesi interne.
- Successivamente, risolviamo le parentesi esterne.
- Semplifichiamo entrambi i lati dell’uguaglianza e raccogliamo termini simili.
- Isoliamo x e calcoliamo il suo valore.
quarto esercizio
In questo esercizio cominciamo a vedere le frazioni, che sono probabilmente l’elemento più complicato delle equazioni lineari. Anche se non preoccuparti perché se hai letto la teoria saprai perfettamente come farlo:
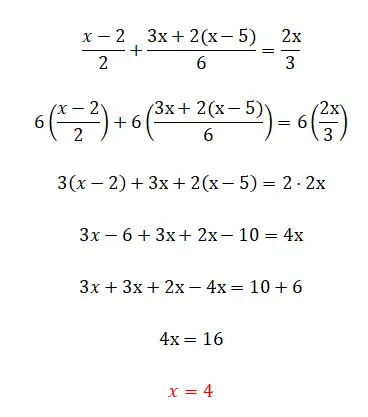
Quinto esercizio
In questo quinto esercizio vediamo le frazioni tra parentesi, il che significa che la gerarchia risolutiva diventa un po’ complicata. Vale la pena ricordare che questo esempio può essere risolto utilizzando due metodi: utilizzando il metodo dei minimi comuni multipli o operando direttamente con le frazioni. Di seguito potete vedere le due procedure complete:
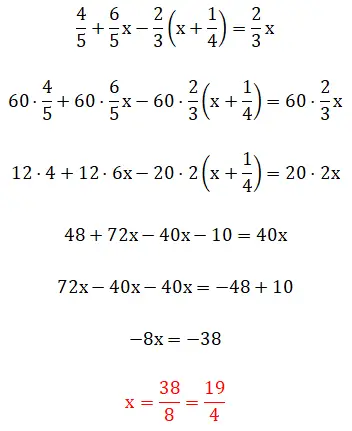
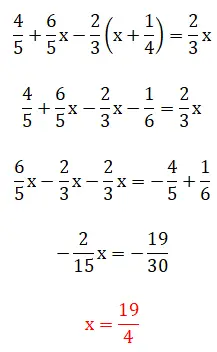
sesto esercizio
Successivamente andremo un po’ oltre con l’argomento delle frazioni e delle parentesi, poiché abbiamo le parentesi annidate. Questo esercizio non porta molte più complicazioni rispetto al precedente, è semplicemente un po’ più difficile in termini di calcoli e basta.
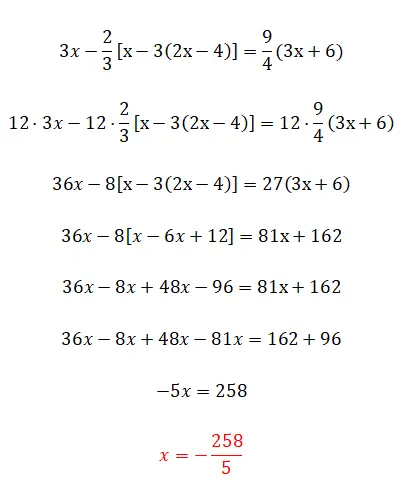
- Moltiplichiamo tutti i termini per lcmp dei denominatori.
- Semplifichiamo l’espressione eliminando le parentesi: prima quelle interne poi quelle esterne.
- Raggruppiamo termini simili su ciascun lato.
- Risolviamo le operazioni su ciascun lato.
- E calcoliamo il valore dell’ignoto.
settimo esercizio
Il seguente esercizio può sembrare molto semplice, ma ti consigliamo di provare comunque a risolverlo, poiché sicuramente ti darà un risultato un po’ insolito. Dopo averlo provato, guarda la soluzione e la spiegazione sotto l’esercizio.
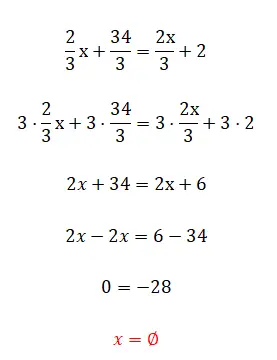
- Moltiplichiamo tutte le frazioni per i lcm dei denominatori.
- Semplifichiamo l’espressione ottenuta.
- E finalmente vediamo che ci dà una falsa uguaglianza, poiché abbiamo eliminato l’ignoto.
Come avrai notato, si tratta di una falsa uguaglianza o di un’uguaglianza senza risultato, poiché non esiste alcun valore che completi correttamente l’equazione. Questo è uno dei casi di cui abbiamo parlato nell’introduzione.
ottavo esercizio
Infine, ti proponiamo questo esercizio che è abbastanza complicato perché presenta tutte le complicazioni che abbiamo visto in questo articolo, anche se ha anche un piccolo trucco. Commenta che se riesci a risolvere questa equazione di primo grado, allora hai compreso perfettamente l’intera teoria. In caso contrario, non preoccuparti, perché questo esercizio è piuttosto complicato.
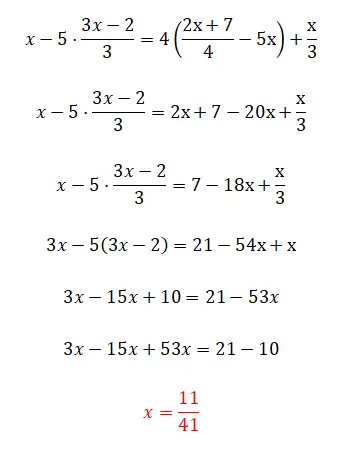
- Iniziamo eliminando i quattro sul lato destro dell’equazione.
- Quindi uniamo le x sul lato destro.
- Moltiplichiamo tutti i termini per tre, in modo da eliminare i denominatori.
- Togliamo le parentesi.
- Mettiamo insieme termini simili.
- Calcoliamo il valore dell’ignoto.
Altri esercizi sulle equazioni lineari
Ora che hai abbastanza pratica, dovresti essere in grado di risolvere equazioni lineari complesse . Tuttavia, se vuoi continuare a esercitarti, ti consigliamo di provare a risolvere questo foglio di lavoro . Ma se ritieni di aver trattato abbastanza, possiamo anche proporti un articolo che può aiutarti a comprendere la gerarchia delle operazioni . In questo modo saprai sempre quale calcolo risolvere per primo e non commetterai mai errori .