Equazioni di linea -

Qui troverai le formule per tutti i tipi di equazioni della retta. Inoltre, potrai vedere esempi di come vengono calcolati e, inoltre, esercitarti con esercizi risolti delle equazioni della retta.

Quali sono tutte le equazioni della retta?

Ricorda che la definizione matematica di linea è un insieme di punti consecutivi rappresentati nella stessa direzione senza curve o angoli.

Quindi, per esprimere analiticamente una qualsiasi retta nel piano (in R2) utilizziamo le equazioni della retta, e per trovarle basta un punto appartenente alla retta e il vettore direzione di detta retta. Solo con questi due elementi geometrici si possono trovare assolutamente tutte le diverse equazioni della retta, che sono le seguenti:

Le equazioni della retta sono l’equazione vettoriale, le equazioni parametriche, l’equazione continua, l’equazione implicita (o generale), l’equazione esplicita, l’equazione punto-pendenza e l’equazione canonica (o segmentale).

Tutti i tipi di equazioni di linea hanno lo stesso obiettivo: rappresentare matematicamente una linea. Ma ogni equazione della retta ha le sue proprietà e quindi, a seconda del problema, è meglio utilizzare l’una o l’altra.

Una volta visto il concetto di equazioni di linea, passiamo ora ad analizzare le caratteristiche di ciascun tipo di equazione di linea in particolare. Di seguito hai una spiegazione dettagliata dei diversi tipi di equazioni della riga, ma se vuoi puoi andare direttamente alla fine della tabella riassuntiva con le formule di tutte le equazioni della riga .

Equazione vettoriale della retta

Sì

$\vv{\text{v}}$

è il vettore direzione della linea e

$P$

un punto che appartiene a destra:

$\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P}_1,P_2)$

La formula per l’equazione vettoriale della retta è:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2) \end{empheq}$

Oro:

$x$

E

$y$

sono le coordinate cartesiane di ogni punto della retta.
$P_1$

E

$P_2$

sono le coordinate di un punto noto facente parte della linea

$P(P}_1,P_2).$
$\text{v}_1$

E

$\text{v}_2$

sono le componenti del vettore direzione della linea

$\vv{\text{v}}=(\text{v}_1,\text{v}_2).$
$t$

è uno scalare (un numero reale) il cui valore dipende da ciascun punto della linea.

È l’equazione vettoriale della retta nel piano, cioè quando si lavora con punti e vettori di 2 coordinate (in R2). Tuttavia, se eseguissimo i calcoli nello spazio (in R3), dovremmo aggiungere un’ulteriore componente all’equazione della retta:

$(x,y,z)=(P_1,P_2,P_3)+t\cdot (\text{v}_1,\text{v}_2,\text{v}_3)$

Equazioni parametriche della retta

Le equazioni parametriche di una linea possono essere ottenute dalla sua equazione vettoriale:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

Per prima cosa moltiplichiamo il parametro

$t$

dal vettore direzione di destra:

$(x,y)=(P_1,P_2)+ (t\cdot\text{v}_1,t\cdot\text{v}_2)$

Successivamente, aggiungiamo le coordinate X e Y:

$(x,y)=(P_1+t\cdot\text{v}_1,P_2+t\cdot\text{v}_2)$

E, infine, cancellando ciascuna variabile separatamente, otteniamo le equazioni parametriche della linea:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases} \end{empheq}$

Oro:

$x$

E

$y$

sono le coordinate cartesiane di ogni punto della retta.
$P_1$

E

$P_2$

sono le coordinate di un punto noto facente parte della linea

$P(P}_1,P_2).$
$\text{v}_1$

E

$\text{v}_2$

sono le componenti del vettore direzione della linea

$\vv{\text{v}}=(\text{v}_1,\text{v}_2).$
$t$

è uno scalare (un numero reale) il cui valore dipende da ciascun punto della linea.

Come prima, queste sono le equazioni parametriche della retta nel piano (in R2), ma per trovare le equazioni parametriche della retta nello spazio (in R3) sarebbe necessario aggiungere un’altra equazione per la terza variabile Z:

$\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \\[1.7ex] z=P_3+t\cdot\text{v}_3\end{cases}$

Equazione continua della retta

L’equazione continua di qualsiasi linea può essere dedotta dalle sue equazioni parametriche:

$\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

Se cancelliamo l’impostazione

$t$

da ciascuna equazione parametrica si ottengono le seguenti espressioni:

$t =\cfrac{x-P_1}{\text{v}_1}}$

$t =\cfrac{y-P_2}{\text{v}_2}}$

E Uguagliando le due equazioni risultanti, otteniamo l’equazione continua della retta:

$t= t$

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

In breve, l’ equazione continua della retta è:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2} \end{empheq}$

Oro:

$x$

E

$y$

sono le coordinate cartesiane di ogni punto della retta.
$P_1$

E

$P_2$

sono le coordinate di un punto noto facente parte della linea

$P(P}_1,P_2).$
$\text{v}_1$

E

$\text{v}_2$

sono le componenti del vettore direzione della linea

$\vv{\text{v}}=(\text{v}_1,\text{v}_2).$

Questa formula serve per l’equazione continua della linea quando si lavora in 2 dimensioni (in 2D). Ma se eseguissimo operazioni in 3 dimensioni (3D), dovremmo aggiungere un componente aggiuntivo all’equazione della linea:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}= \cfrac{z-P_3}{\text{v}_3}$

Equazione implicita o generale della retta

Sì

$\vv{\text{v}}$

è il vettore direzione della linea e

$P$

un punto che appartiene a destra:

$\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P}_1,P_2)$

La formula per l’ equazione implicita, generale o cartesiana della retta è:

Oro:

$x$

E

$y$

sono le coordinate cartesiane di ogni punto della retta.
il coefficiente
$A$

è la seconda componente del vettore direzione della retta:

$A=\text{v}_2}$
il coefficiente
$B$

è la prima componente del vettore di direzione cambiato segno:

$B=-\text{v}_1}$
il coefficiente
$C$

viene calcolato sostituendo il punto noto

$P$

nell’equazione della retta.

la formula, l’equazione implicita di una retta si può ottenere anche moltiplicando le frazioni dell’equazione continua.

Equazione esplicita della retta

La formula per l’ equazione esplicita della retta è:

Oro:

$m$

è la pendenza della retta.
$n$

la sua intercetta y, cioè l’altezza alla quale interseca l’asse Y.

Nella sezione seguente vedrai come vengono determinati i parametri

$m$

$n$

della retta Ma, in particolare, un altro modo per trovare l’equazione esplicita è utilizzare l’equazione implicita; per questo, l’incognita deve essere risolta

$y$

dell’equazione implicita.

Significato dei parametri m e n

Come abbiamo visto nella definizione dell’equazione esplicita della retta, il parametro

$m$

è la pendenza della retta e

$n$

la sua intercetta y. Ma cosa significa? Vediamolo dalla rappresentazione grafica di una linea:

Qual è l'equazione esplicita della retta y=mx+b

Il termine indipendente

$\bm{n}$

è il punto di intersezione della linea con l’asse del computer (asse OY). Ad esempio, nel grafico sopra

$n$

è uguale a 1 perché la linea interseca l’asse y in y=1.

D’altra parte, il termine

$\bm{m}$

indica la pendenza della retta , cioè la sua inclinazione. Come vedi nel grafico,

$m$

è uguale a 2 poiché la linea sale di 2 unità verticali per 1 unità orizzontale.

Ovviamente se la pendenza è positiva la funzione è crescente (sale), invece se la pendenza è negativa la funzione è decrescente (scende).

Calcolare la pendenza di una retta

Una volta che sappiamo esattamente qual è la pendenza di una retta, vediamo come viene calcolata. Pertanto, ci sono 3 modi diversi per determinare numericamente la pendenza di una linea:

Dati due punti diversi sulla retta
$P_1(x_1,y_1)$

E

$P_2(x_2,y_2),$

La pendenza della retta è pari a:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

Sì
$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

è il vettore direzione della retta, la sua pendenza è:

$m = \cfrac{\text{v}_2}{\text{v}_1}$

Sì
$\alpha$

è l’angolo formato dalla retta con l’asse delle ascisse (asse X), la pendenza della retta è equivalente alla tangente di detto angolo:

$m = \text{tg}(\alpha )$

formula per l'equazione esplicita della retta

Equazione punto-pendenza della retta

La formula per l’ equazione punto-pendenza della retta è:

Oro:

$m$

è la pendenza della retta.
$P_1, P_2$

sono le coordinate di un punto sulla retta

$P(P_1,P_2).$

Equazione canonica o segmentale della retta

Sebbene questa variante dell’equazione della retta sia meno conosciuta, l’equazione canonica della retta si può ottenere dai punti di intersezione della retta con gli assi cartesiani.

Siano i due punti di intersezione con gli assi di una data retta:

Tagliare con l’asse X:

$(a,0)$

Taglio con asse Y:

$(0,b)$

La formula per l’equazione canonica della retta è:

In matematica, l’equazione canonica della retta è anche chiamata equazione segmentale o equazione simmetrica.

D’altra parte, i coefficienti

$a$

$b$

Possono anche essere trovati dall’equazione generale della retta utilizzando le seguenti formule:

$Ax+By+C=0$

$a = -\cfrac{C}{A} \qquad \qquad b = -\cfrac{C}{B}$

Tutte le equazioni della retta (formule)

Riassumendo, ecco una tabella in cui sono riportate le formule di tutte le equazioni della retta:

Esempio di calcolo delle equazioni della retta

Ora che abbiamo visto tutta la spiegazione dell’equazione della retta, vediamo come si risolve un tipico problema delle equazioni della retta:

Trova tutte le equazioni della retta determinata dal punto
$P$

e il vettore

$\vv{\text{v}}.$

$P(3,-1) \qquad \qquad \vv{\text{v}}=(2,4)$

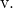
Innanzitutto troviamo l’equazione vettoriale della retta dalla sua formula:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

Sostituisci semplicemente le coordinate del punto e il vettore nella formula:

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(3,-1)+t\cdot (2,4)} \quad \vphantom{\Bigl(}}$

In secondo luogo, troviamo le equazioni parametriche della retta attraverso la sua formula corrispondente:

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=3+2t} \\[1.7ex] \bm{y=-1+4t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

E determiniamo anche l’equazione continua della retta con la sua formula:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-3}{2}=\cfrac{y-(-1)}{4}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x-3}}{\bm{2}}\bm{=}\cfrac{\bm{y+1}}{\bm{4}}\quad \vphantom{\Biggl(}}$

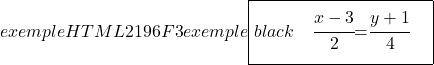
Come hai visto, le equazioni vettoriali, parametriche e continue sono facili da calcolare, basta utilizzare le rispettive formule.

Passiamo ora alla ricerca dell’equazione generale (o implicita) della retta. Per fare ciò, incrociamo le due frazioni dell’equazione continua:

$4\cdot (x-3)= 2 \cdot (y+1)$

$4x-12= 2y+2$

$4x-12-2y-2=0$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{4x-2y-14=0}\quad \vphantom{\Bigl(}}$

Ora possiamo determinare l’equazione esplicita della retta risolvendo l’incognita

$y$

dell’equazione implicita:

$4x-2y-14=0$

$-2y=-4x+14$

$y=\cfrac{-4x+14}{-2}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=2x-7}\quad \vphantom{\Bigl(}}$

Pertanto la pendenza della retta è pari a 2 (termine che accompagna la variabile indipendente

$x$

$m=2$

E con questo possiamo calcolare l’equazione punto-pendenza della retta con la sua formula:

$y-P_2=m(x-P_1)$

$y-(-1)=2(x-3)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y+1=2(x-3)}\quad \vphantom{\Bigl(}}$

Infine, per trovare l’equazione segmentale della retta calcoliamo i suoi punti di intersezione con gli assi OX e OY quindi applichiamo la sua formula:

$y=2x-7$

Punto di intersezione con l’asse delle ascisse (asse X)

$y=0$

$0=2x-7$

$-2x=-7$

$x=\cfrac{-7}{-2} = \cfrac{7}{2}$

$\displaystyle \left(\frac{7}{2}, 0\right)$

Punto di intersezione con l’asse y (asse Y)

$x=0$

$y=2\cdot 0-7$

$y=-7$

$\displaystyle \left(0,-7\right)$

$\cfrac{x}{a}+\cfrac{y}{b} = 1$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\cfrac{\bm{x}}{\frac{\bm{7}}{\bm{2}}}+\cfrac{\bm{y}}{\bm{-7}} \bm{= 1} \quad \vphantom{\Biggl(}}$

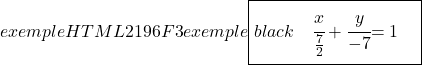
Equazione della retta passante per due punti

Un altro problema molto comune nelle equazioni delle rette è trovare l’equazione della retta determinata da due punti dati. Sebbene possiamo calcolare il vettore direzione della linea con i 2 punti e quindi l’equazione, di seguito ti forniamo una formula con la quale puoi trovare direttamente e facilmente l’equazione di detta linea.

Considera due punti situati su una linea:

$P_1(x_1,y_1) \qquad \qquad P_2(x_2,y_2)$

La formula per trovare l’equazione della retta dai suoi 2 punti è:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} y-y_1= \cfrac{y_2-y_1}{x_2-x_1} (x-x_1) \end{empheq}$

Questa formula ci permette di calcolare direttamente l’equazione punto-pendenza della retta quando ci vengono dati 2 punti attraverso i quali passa la retta.

Risolti problemi di equazioni della retta

Esercizio 1

Trova l’equazione vettoriale, le equazioni parametriche e l’equazione continua della linea definita dal punto

$P$

e il suo vettore direttivo

$\vv{\text{v}}.$

Sii entrambi:

$P(0,3) \qquad \qquad \vv{\text{v}}=(-1,5)$

vedi soluzione

Innanzitutto, calcoliamo l’equazione vettoriale della retta dalla sua formula:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(0,3)+t\cdot (-1,5)} \quad \vphantom{\Bigl(}}$

Troviamo quindi le equazioni parametriche della retta utilizzando la formula corrispondente:

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\begin{cases} x=0+t\cdot (-1) \\[1.7ex] y=3+t\cdot 5\end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-t} \\[1.7ex] \bm{y=3+5t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

E, infine, determiniamo l’equazione continua della retta con la rispettiva formula:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-0}{-1}=\cfrac{y-3}{5}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x}}{\bm{-1}}\bm{=}\cfrac{\bm{y-3}}{\bm{5}}\quad \vphantom{\Biggl(}}$

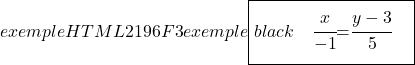
Esercizio 2

Trova l’equazione implicita, l’equazione esplicita e l’equazione punto-pendenza della linea determinata dal punto

$P$

e il suo vettore di direzione è

$\vv{\text{v}}.$

$P(-4,3) \qquad \qquad \vv{\text{v}}=(2,6)$

vedi soluzione

La formula per l’equazione implicita della retta è:

$Ax+By+C=0$

Dobbiamo quindi trovare i coefficienti A, B e C. Le incognite A e B si ottengono dalle coordinate del vettore direzione della retta, perché è sempre verificata la seguente uguaglianza:

$\vv{\text{v}}= (-B,A)$

Di conseguenza, il coefficiente A è la seconda coordinata del vettore, e il coefficiente B è la prima coordinata del vettore cambiato segno:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}= (2,6) \end{array} \right\}\longrightarrow \begin{array}{l}A=6 \\[2ex] B=-2 \end{array}$

Dobbiamo quindi trovare solo il coefficiente C. Per fare ciò, dobbiamo sostituire nella sua equazione il punto che sappiamo appartenere alla retta:

$P(-4,3)$

$6x-2y+C=0 \ \xrightarrow{x=-4 \ ; \ y=3} \ 6\cdot (-4)-2\cdot 3+C=0$

$-24-6+C=0$

$-30+C=0$

$C=30$

Quindi l’equazione implicita, generale o cartesiana della retta è:

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{6x-2y+30=0}\quad \vphantom{\Bigl(}}$

Ora possiamo determinare l’equazione esplicita della retta risolvendo l’incognita

$y$

dell’equazione implicita:

$6x-2y+30=0$

$-2y=-6x-30$

$y=\cfrac{-6x-30}{-2}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=3x+15}\quad \vphantom{\Bigl(}}$

Pertanto la pendenza della retta è pari a 3 (termine prima della variabile indipendente

$x$

$m=3$

E, dal valore della pendenza della retta, possiamo calcolare l’equazione punto-pendenza della retta con la sua formula:

$y-P_2=m(x-P_1)$

$y-3=3(x-(-4))$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y-3=3(x+4)}\quad \vphantom{\Bigl(}}$

Esercizio 3

Determina 3 punti sulla riga seguente, espressi come equazione implicita o generale:

$4x+2y-8 = 0$

vedi soluzione

Per calcolare un punto su una linea, dobbiamo semplicemente assegnare un valore a una delle variabili e poi trovare il valore dell’altra variabile in quel punto.

Calcoliamo un primo punto facendo

$x=0:$

$4\cdot 0+2y-8 = 0$

$2y = 8$

$y = \cfrac{8}{2}$

$y = 4$

$\bm{P_1(0,4)}$

Troviamo quindi un secondo punto che dà un altro valore alla variabile

$x,$

Per esempio

$x=1:$

$4\cdot 1+2y-8 = 0$

$2y = 8-4$

$2y = 4$

$y = \cfrac{4}{2}$

$y = 2$

$\bm{P_2(1,2)}$

E, infine, calcoliamo un terzo punto risolvendo

$x=2:$

$4\cdot 2+2y-8 = 0$

$2y = 8-8$

$2y = 0$

$y = \cfrac{0}{2}$

$y = 0$

$\bm{P_3(2,0)}$

Esercizio 4

Trova tutte le equazioni della retta definita dal punto

$P$

e il vettore

$\vv{\text{v}}.$

$P(-1,4) \qquad \qquad \vv{\text{v}}=(-3,6)$

vedi soluzione

Innanzitutto troviamo l’equazione vettoriale della retta dalla sua formula:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(-1,4)+t\cdot (-3,6)} \quad \vphantom{\Bigl(}}$

In secondo luogo, troviamo le equazioni parametriche della retta attraverso la sua formula corrispondente:

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-1-3t} \\[1.7ex] \bm{y=4+6t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

E determiniamo anche l’equazione continua della linea usando la sua formula:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-(-1)}{-3}=\cfrac{y-4}{6}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x+1}}{\bm{-3}}\bm{=}\cfrac{\bm{y-4}}{\bm{6}}\quad \vphantom{\Biggl(}}$

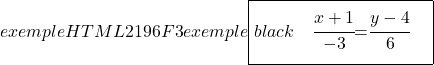
Passiamo ora a trovare l’equazione implicita o generale della retta. Per fare ciò, incrociamo le due frazioni dell’equazione continua:

$6\cdot (x+1)= -3 \cdot (y-4)$

$6x+6= -3y+12$

$6x+6+3y-12=0$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{6x+3y-6=0}\quad \vphantom{\Bigl(}}$

Ora possiamo determinare l’equazione esplicita della retta risolvendo l’incognita

$y$

dell’equazione implicita:

$6x+3y-6=0$

$3y=-6x+6$

$y=\cfrac{-6x+6}{3}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=-2x+2}\quad \vphantom{\Bigl(}}$

Pertanto la pendenza della retta equivale a -2 (termine che accompagna la variabile indipendente

$x$

$m=-2$

E con questo possiamo calcolare l’equazione punto-pendenza della retta con la sua formula:

$y-P_2=m(x-P_1)$

$y-4=-2(x-(-1))$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y-4=-2(x+1)}\quad \vphantom{\Bigl(}}$

Infine, per trovare l’equazione segmentale della retta, calcoliamo i punti di intersezione della retta con gli assi OX e OY quindi utilizziamo la sua formula:

$y=-2x+2$

Punto di intersezione con l’asse delle ascisse (asse X)

$y=0$

$0=-2x+2$

$2x=2$

$x=\cfrac{2}{2} =1$

$\displaystyle \left(1, 0\right)$

Punto di intersezione con l’asse y (asse Y)

$x=0$

$y=-2\cdot 0+2$

$y=2$

$\displaystyle \left(0,2\right)$

$\cfrac{x}{a}+\cfrac{y}{b} = 1$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\cfrac{\bm{x}}{\bm{1}}+\cfrac{\bm{y}}{\bm{2}} \bm{= 1} \quad \vphantom{\Biggl(}}$

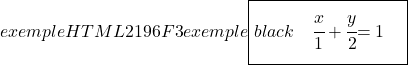
Esercizio 5

Trova l’equazione della retta che passa per i seguenti due punti:

$P_1 (4,-1) \qquad \qquad P_2(5,2)$

vedi soluzione

Poiché conosciamo già due punti sulla retta, applichiamo direttamente la formula per l’equazione della retta a 2 punti dati:

$y-y_1= \cfrac{y_2-y_1}{x_2-x_1} (x-x_1)$

Ora sostituiamo le coordinate cartesiane dei punti nella formula:

$y-(-1)= \cfrac{2-(-1)}{5-4} (x-4)$

E, infine, calcoliamo la pendenza della retta:

$y+1= \cfrac{3}{1} (x-4)$

$y+1= 3(x-4)$

L’equazione della retta che passa per questi due punti è quindi:

$\bm{y+1= 3(x-4)}$

Quali sono tutte le equazioni della retta?

Equazione vettoriale della retta

Equazioni parametriche della retta

Equazione continua della retta

Equazione implicita o generale della retta

Equazione esplicita della retta

Significato dei parametri m e n

Calcolare la pendenza di una retta

Equazione punto-pendenza della retta

Equazione canonica o segmentale della retta

Tutte le equazioni della retta (formule)

Esempio di calcolo delle equazioni della retta

Equazione della retta passante per due punti

Risolti problemi di equazioni della retta

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Lascia un commento Annulla risposta