Equazione della linea tangente -

In questo articolo vedremo come trovare l’equazione della tangente ad una curva. Inoltre, puoi allenarti con esercizi risolti di diversi livelli di difficoltà.

Equazione della retta tangente ad una funzione in un punto

L’ equazione della tangente alla funzione f(x) nel punto x=x ₀ è:

$y -y_0= m(x-x_0)$

Dove il punto P(x ₀ ,y ₀ ) è il punto in cui la tangente e la funzione coincidono. E la pendenza della tangente, m, è uguale alla derivata della curva nel punto x ₀ , cioè m=f'(x ₀ ).

Nell’immagine sopra puoi vedere una curva

$f(x)$

rappresentato in blu e una linea arancione tangente alla funzione

$f(x)$

$x=x_0$

, poiché hanno solo questo punto in comune. Bene, l’equazione di questa tangente è

$y -y_0= m(x-x_0)$

, e la sua pendenza è

$m=f'(x_0)$

Come trovare l’equazione della tangente

Per trovare l’equazione della tangente ad una funzione in un punto, devi fare:

Trova la pendenza della linea tangente calcolando la derivata della funzione nel punto di tangenza.
Determinare un punto sulla retta tangente.
Trova l’equazione della linea tangente utilizzando la pendenza calcolata e il punto della linea tangente.

Esempio dell’equazione della tangente ad una curva

Una volta vista la teoria sull’equazione della tangente, vediamo come calcolare l’equazione di una tangente risolvendo passo dopo passo un esempio:

Calcolare l’equazione della tangente alla curva
$f(x)=x^2+x$

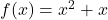
Di

$x=1$

.

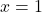
Sappiamo che l’equazione della tangente è sempre della forma seguente:

$y -y_0= m(x-x_0)$

La prima cosa da fare è calcolare la pendenza della retta. Pertanto, la pendenza della tangente,

$m$

, sarà il valore della derivata della curva nel punto di tangenza x=1, cioè

$m=f'(1).$

Pertanto differenziamo la funzione e poi calcoliamo

$f'(1):$

$f(x)=x^2+x \quad \longrightarrow \quad f'(x)=2x+1$

$f'(1)= 2\cdot 1+1=2+1=3$

$m=f'(1)=3$

Una volta che conosciamo il valore di

$m$

, dobbiamo trovare un punto

$(x_0,y_0)$

della retta tangente per completare l’equazione della retta tangente.

L’ equazione della tangente e della curva hanno sempre un punto in comune , che in questo caso è

$x=1$

. Quindi, come la curva

$f(x)$

passa per questo punto, possiamo trovare l’altra componente del punto facendo il calcolo

$f(1):$

$f(x)=x^2+x$

$f(1)=1^2+1=2$

Il punto di tangenza è quindi:

$P(1,2)$

Sia la curva che la tangente passano per questo punto, quindi possiamo usarlo anche per trovare l’equazione della tangente.

Non resta che sostituire i valori trovati della pendenza e del punto della tangente nella sua equazione:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=3 \qquad P(1,2) \end{array} \right\} \longrightarrow \ y -2= 3(x-1)$

In breve, l’equazione della tangente è:

$\bm{y-2=3(x-1)}$

Puoi anche esprimere l’equazione della retta tangente con l’equazione esplicita della retta:

$\bm{y=3x-1}$

Sotto potete vedere la curva rappresentata

$f(x)=x^2+x$

e la sua retta tangente a

$x=1,$

$y-2=3(x-1):$

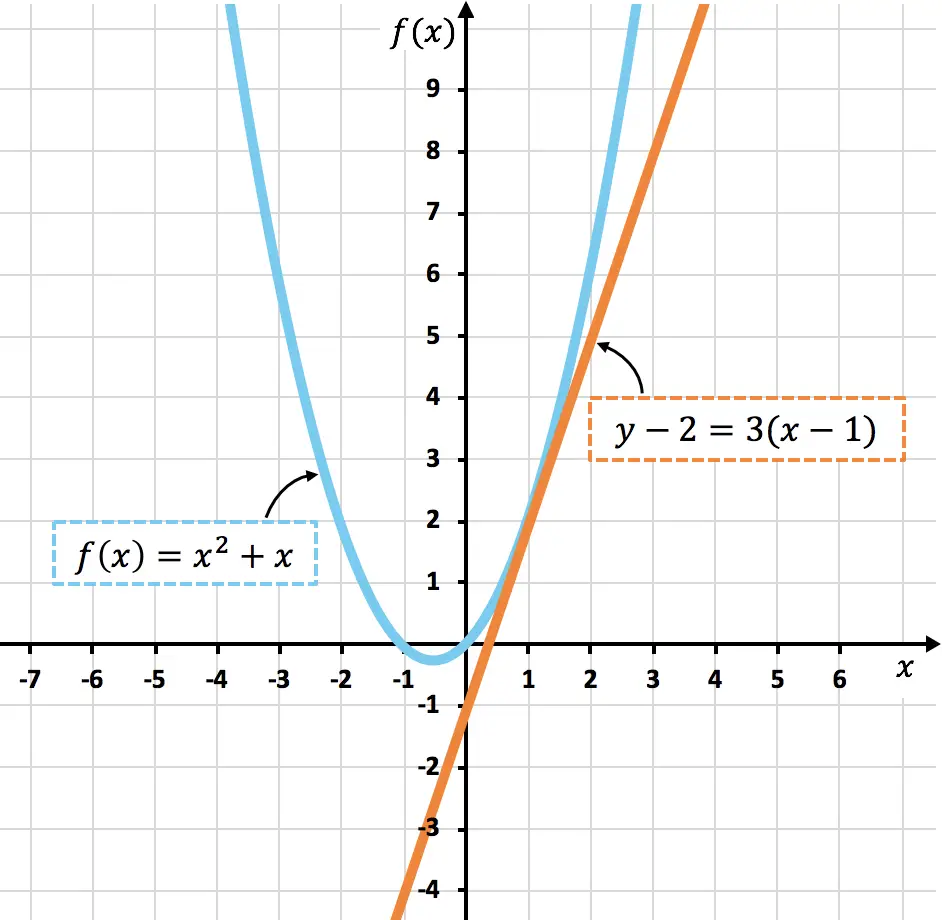
equazione della retta tangente ad una curva in un punto

Come puoi vedere, la curva

$f(x)=x^2+x$

e la tangente

$y-2=3(x-1)$

hanno in comune solo il punto

$(1,2)$

, esattamente come avevamo calcolato.

Esercizi risolti sull’equazione della tangente

Esercizio 1

Calcolare l’equazione della tangente alla curva

$f(x)=2x^2-4x+3$

$x=2 .$

Vedi la soluzione

L’equazione della tangente sarà sempre della forma seguente:

$y-y_0=m(x-x_0)$

Passaggio 1: calcolare la pendenza della linea tangente

La pendenza, m , è il valore della derivata della curva nel punto di tangenza. Pertanto, in questo caso

$m = f'(2):$

$f(x)=2x^2-4x+3 \ \longrightarrow \ f'(x)= 4x-4$

$f'(2)= 4\cdot 2-4=8-4=4$

$m=f'(2)=4$

Passaggio 2: trova un punto sulla linea tangente

L’equazione della tangente e della curva hanno sempre un punto in comune, che in questo caso è

$x=2$

. Quindi, come la curva

$f(x)$

passa per questo punto, possiamo trovare l’altra componente del punto facendo il calcolo

$f(2):$

$f(x)=2x^2-4x+3$

$f(2)=2\cdot 2^2-4\cdot 2+3 =2 \cdot 4 -8 +3 = 3$

Pertanto, il punto attraverso il quale passano sia la curva che la tangente è il punto

$(2,3).$

Passaggio 3: scrivere l’equazione della tangente

Non resta che sostituire i valori trovati della pendenza e del punto della tangente nella sua equazione:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(2,3) \end{array} \right\} \longrightarrow \ y -3= 4(x-2)$

L’equazione della tangente è quindi:

$\bm{y -3= 4(x-2)}$

Esercizio 2

Calcolare l’equazione della tangente alla curva

$\displaystyle f(x)=-3x^2+2x$

all’origine delle coordinate.

Vedi la soluzione

L’origine delle coordinate si riferisce al punto

$(0,0).$

Dobbiamo quindi calcolare la tangente alla funzione in quel punto

$(0,0) .$

Per prima cosa determiniamo il valore della pendenza della tangente calcolando la derivata all’origine delle coordinate:

$f(x)=-3x^2+2x \ \longrightarrow \ f'(x)= -6x+2$

$f'(0)= -6\cdot 0+2=2$

$m=f'(0)=2$

In questo caso conosciamo già il punto attraverso il quale passa la tangente. Perché l’affermazione ci dice che la retta deve essere tangente alla curva nell’origine delle coordinate, cioè nel punto

$(0,0).$

Quindi il punto in cui la curva e la tangente condividono è il punto

$(0,0).$

Infine, sostituisci semplicemente i valori trovati per la pendenza e il punto della tangente nella tua equazione:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=2 \qquad P(0,0) \end{array} \right\} \longrightarrow \ y -0= 2(x-0)$

In conclusione, l’equazione della tangente è:

$y -0= 2(x-0)$

$\bm{y = 2x}$

Esercizio 3

Calcola la linea tangente alla curva

$f(x)=x^2-2x-1$

che è parallelo a destra

$y-4x-6=0$

Vedi la soluzione

In questo problema ci viene detto che la tangente deve essere parallela alla retta

$y-4x-6=0 .$

E due rette sono parallele se hanno la stessa pendenza. La tangente deve quindi avere la stessa pendenza della retta

$y-4x-6=0.$

Ciò significa che dobbiamo trovare la pendenza della retta

$y-4x-6=0 .$

Per fare ciò, cancelliamo la variabile e:

$y-4x-6=0 \ \longrightarrow \ y =4x+6$

Quindi la pendenza della retta

$y=4x+5$

è 4, poiché la pendenza di una linea è il numero che moltiplica la x quando la y è chiara.

Quindi anche la pendenza della tangente deve essere 4, perché per essere parallele devono avere la stessa pendenza.

$m=4$

In questo caso non ci dicono il punto di tangenza tra la curva e la tangente. Ma sappiamo che la derivata della curva nel punto di tangenza è uguale alla pendenza della tangente, cioè

$m=f'(x_0)$

. Ebbene, come possiamo conoscere il valore di

$m$

, possiamo trovare x ₀ dall’equazione

$m=f'(x_0):$

Per fare ciò, calcoliamo prima la derivata di

$f(x):$

$f(x)= x^2-2x-1 \ \longrightarrow \ f'(x)=2x-2$

E ora risolviamo

$m=f'(x_0)$

sapendo che

$m = 4 :$

$m =f'(x_0)$

$4 =2(x_0)-2$

$4+2 =2x_0$

$6 =2x_0$

$\cfrac{6}{2} =x_0$

$3=x_0$

E una volta che conosciamo la coordinata x del punto, possiamo trovare l’altra coordinata del punto eseguendo i calcoli

$f(3):$

$f(3)=3^2-2\cdot 3-1= 9-6-1=2$

Pertanto, il punto attraverso il quale passano sia la curva che la tangente è il punto

$(3,2).$

Non resta che sostituire i valori trovati della pendenza e del punto della tangente nella sua equazione:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(3,2) \end{array} \right\} \longrightarrow \ y -2= 4(x-3)$

E l’equazione della tangente è:

$\bm{y -2=4(x-3)}$

Esercizio 4

Calcola la linea tangente alla curva

$f(x)=2x^2+5x+1$

che forma un angolo di 45º con l’asse X.

Vedi la soluzione

La formulazione del problema ci dice che la linea tangente deve formare un angolo di 45º con l’asse X. In questi casi è necessario applicare la seguente formula per trovare il valore della pendenza:

$m = \text{tg}\left(\alpha\right)$

$m = \text{tg}\left(45^{\text{o}}\right) = 1$

La dichiarazione non specifica il punto di tangenza tra la curva e la linea tangente. Ma sappiamo che la derivata della curva nel punto di tangenza è equivalente alla pendenza della tangente, cioè

$m=f'(x_0)$

. Possiamo quindi calcolare x ₀ risolvendo l’equazione

$m=f'(x_0):$

Per fare ciò, calcoliamo prima la derivata di

$f(x):$

$f(x)=2x^2+5x+1\ \longrightarrow \ f'(x)=4x+5$