Qui troverai come viene calcolata l’equazione (formula) dell’ellisse, indipendentemente dal fatto che abbia l’origine come centro o meno. Troverai anche quali sono gli elementi dell’ellisse, come calcolarli e a cosa servono. Inoltre, potrai vedere esempi ed esercizi risolti di equazioni dell’ellisse.
Formula dell’equazione dell’ellisse
La formula per l’ equazione dell’ellisse in coordinate cartesiane è:
![]()
Oro:
-

E

sono le coordinate del centro dell’ellisse:
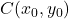
-

è il raggio orizzontale dell’ellisse.
-

è il raggio verticale dell’ellisse.
Equazione dell’ellisse centrata nell’origine
Un tipo molto comune di ellisse è quella il cui centro è all’origine delle coordinate, cioè nel punto (0,0). Ecco perché vedremo come trovare l’equazione dell’ellisse centrata nell’origine.
Seguendo la formula per l’equazione dell’ellisse:
![]()
Se l’ellisse è centrata sull’origine delle coordinate, significa che
![]()
E
![]()
sono uguali a 0, quindi la tua equazione sarà:
![]()
Ci sono matematici che chiamano questa espressione anche equazione canonica o equazione ridotta dell’ellisse.
elementi dell’ellisse
Una volta che vediamo come appare l’equazione dell’ellisse, vedremo quali sono i suoi elementi. Ma prima ricordiamo cos’è esattamente un’ellisse:
L’ellisse è una linea piatta, chiusa, curva, molto simile alla circonferenza, ma la sua forma è più ovale. In particolare, l’ellisse è il luogo di tutti i punti di un piano la cui somma delle distanze da altri due punti fissi (detti fuochi F e F’) è costante.
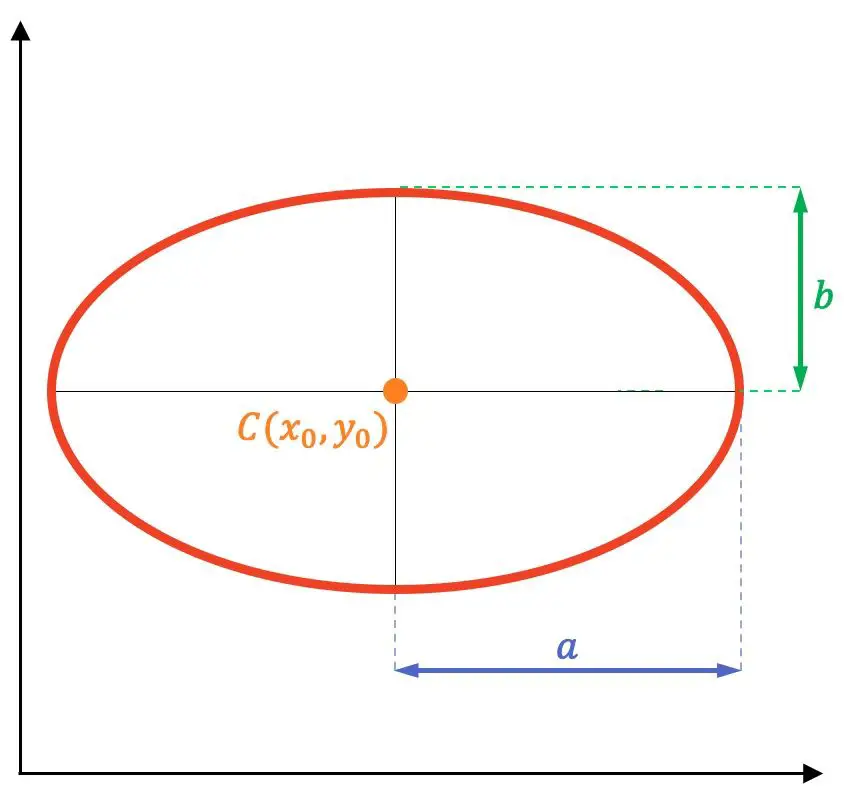
Quindi gli elementi di un’ellisse sono:
- I fuochi : questi sono i punti fissi F e F’ (punti colorati viola nell’immagine sotto). La somma delle distanze tra qualsiasi punto dell’ellisse e ciascun fuoco è costante per tutti i punti dell’ellisse.
- Asse principale o focale : è l’asse di simmetria dell’ellisse in cui si trovano i focali. Chiamato anche asse maggiore.
- Asse secondario : è l’asse di simmetria dell’ellisse perpendicolare all’asse principale. È detto anche asse minore e corrisponde alla bisettrice perpendicolare del segmento che congiunge i fuochi.
- Centro : è il punto di intersezione degli assi dell’ellisse. Inoltre, è il centro di simmetria dell’ellisse (punto arancione sul grafico).
- Vertici : punti di intersezione dell’ellisse con i suoi assi di simmetria (punti neri).
- Semiasse maggiore o asse principale: segmento che va dal centro dell’ellisse ai vertici dell’asse principale.
- Semiasse minore o asse secondario: segmento compreso tra il centro dell’ellisse ed i vertici dell’asse secondario.
- Lunghezza focale : questa è la distanza tra i due punti focali.
- Distanza semifocale : corrisponde alla distanza tra il centro e ciascuno dei punti focali.
- I radiovettori : sono i segmenti che congiungono un qualsiasi punto dell’ellisse ad ogni fuoco (segmenti blu nel grafico).

Relazione tra gli elementi di un’ellisse
I diversi elementi di un’ellisse sono collegati tra loro. Inoltre, le relazioni tra loro sono molto importanti per gli esercizi sulle ellissi, perché di solito sono necessarie per risolvere problemi sulle ellissi e determinare le loro equazioni.
Come abbiamo visto sopra nella definizione dell’ellisse, la distanza da qualsiasi punto dell’ellisse al fuoco F più la distanza dallo stesso punto al fuoco F’ è costante. Ebbene, questo valore costante è pari al doppio di quanto misura il semiasse maggiore. In altre parole, per ogni punto dell’ellisse vale la seguente uguaglianza:
![]()
Oro
![]()
E
![]()
è la distanza dal punto P al fuoco F e F’ rispettivamente e
![]()
è la lunghezza dell’asse semifocale.
Pertanto, poiché il vertice dell’asse secondario si trova proprio al centro dell’asse focale, la distanza da esso a uno dei fuochi è equivalente alla lunghezza dell’asse semiprimario (
![]()
):
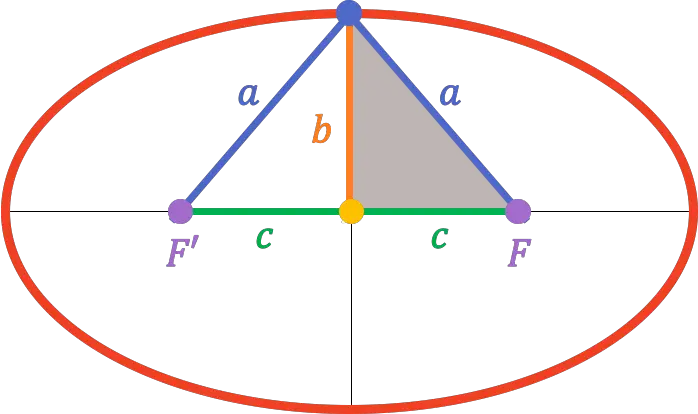
Quindi, dal teorema di Pitagora , è possibile ricavare la relazione che esiste tra il semiasse principale, il semiasse secondario e la semilunghezza focale:
![]()
Ricorda questa formula perché sarà molto utile per calcolare i risultati degli esercizi con i puntini di sospensione.
Eccentricità dell’ellisse
Ovviamente non tutte le ellissi sono uguali, ma alcune sono più allungate ed altre più appiattite. Quindi, esiste un coefficiente che viene utilizzato per misurare quanto è arrotondata una determinata ellisse. Questo coefficiente si chiama eccentricità e si calcola con la seguente formula:
![]()
Oro
![]()
è la distanza dal centro dell’ellisse a uno dei suoi fuochi e
![]()
la lunghezza del semiasse maggiore.
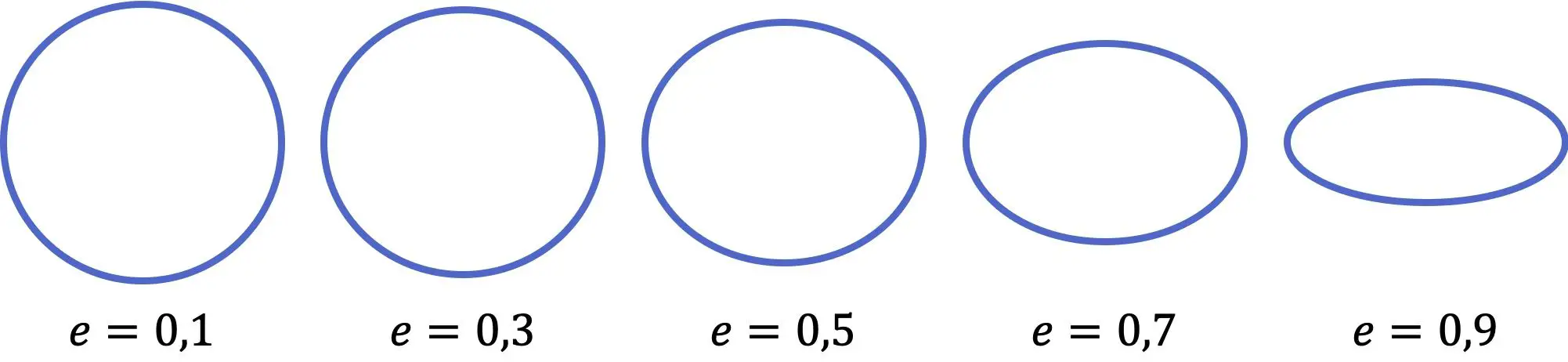
Come puoi vedere nella rappresentazione precedente, minore è il valore dell’eccentricità dell’ellisse, più assomiglia ad un cerchio, invece, maggiore è il coefficiente, più l’ellisse è appiattita. Inoltre, il valore dell’eccentricità varia da zero (cerchio perfetto) a uno (linea orizzontale), entrambi esclusi.

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-4)^2}{5^2 }+\cfrac{(y-(-1))^2}{3^2} = 1\cfrac{\bm{(x-4)^2}}{\bm{25}}+\cfrac{\ bm{(y+1)^2}}{\bm{9}} \bm{= 1}

![]()
\cfrac{(x-2)^2}{6^2}+\cfrac{(y-0)^2}{3^2} = 1\cfrac{\bm{(x-2)^2}} {\bm{36}}+\cfrac{\bm{y^2}}{\bm{9}} \bm{= 1}

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{13^2 }+\cfrac{(y-0)^2}{12^2} = 1\cfrac{\bm{x^2}}{\bm{169}}+\cfrac{\bm{y^2}} {\bm{144}} \bm{= 1}

![]()
d_v=6-(-4) =10 b =\cfrac{10}{2} = 5
![]()
C_x= \cfrac{10+(-4)}{2} = \cfrac{6}{2} =3 C_y= \cfrac{6+(-4)}{2} = \cfrac{2}{ 2} = 1C(3.1)
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-3)^2}{7^2 }+\cfrac{(y-1)^2}{5^2} =1\cfrac{\bm{(x-3)^2}}{\bm{49}}+\cfrac{\bm{( y-1)^2}}{\bm{25}} \bm{= 1}
![]()
a^2=b^2+c^2 c^2=a^2-b^2 c=\sqrt{a^2-b^2} = \sqrt{7^2-5^2}=\sqrt {24}
![]()
\qrt{24}
![]()
C(3,1) \bm{FA\sinistra(3+\quadrato{24},1}\destra)} \bm{FA\sinistra(3-\quadrato{24},1}\destra)}

![]()
d(P,F) + d(P,F’)= 2a 3+5= 2a 8= 2a \cfrac{8}{2}= a 4= a
![]()
a^2=b^2+c^2 b^2=a^2-c^2 b=\sqrt{a^2-c^2} = \sqrt{4^2-3^2}=\sqrt {7}
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{4^2 }+\cfrac{(y-0)^2}{\sinistra(\sqrt{7}\right)^2} =1\cfrac{\bm{x^2}}{\bm{16}}+\ cfrac{\bm{y^2}}{\bm{7}} \bm{= 1}$
Infine, se questo articolo ti è stato utile, sicuramente ti interesseranno anche le nostre pagine sulla formula dell’iperbole e sulla formula della parabola . Troverai una spiegazione dettagliata di cosa sono l’iperbole e la parabola, le loro equazioni, le loro caratteristiche, esempi, esercizi risolti,…