Equazione della circonferenza -

In questa pagina troverai tutto sull’equazione della circonferenza: equazione ordinaria, equazione generale, altri tipi di equazioni della circonferenza, quando l’equazione di una circonferenza è corretta,… Inoltre, vedrai esempi di come trovare l’equazione di una circonferenza e potrete esercitarvi con esercizi risolti.

Equazione ordinaria della circonferenza

Prima di vedere cos’è l’equazione della circonferenza, ricordiamo la nozione di circonferenza:

La circonferenza è il luogo dei punti del piano equidistanti da un punto fisso detto centro.

Pertanto tutti i punti di una circonferenza hanno la stessa distanza dal suo centro.

Inoltre, il cerchio è una delle quattro sezioni coniche insieme all’ellisse, alla parabola e all’iperbole. Cioè, un cerchio può essere ottenuto tagliando un cono con un piano parallelo alla sua base.

Il modo più semplice per descrivere un cerchio nel piano cartesiano è mediante la sua equazione ordinaria. Quindi, la formula per l’equazione ordinaria della circonferenza è la seguente:

L’ equazione ordinaria della circonferenza è:

$(x-a)^2+(y-b)^2=r^2$

Oro:

$r$

è il raggio del cerchio.
$a$

E

$b$

sono le coordinate del centro del cerchio:

$C(a,b)$

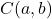
Anche se non lo dimostreremo perché è un po’ noioso, questa equazione può essere ottenuta dal teorema di Pitagora.

Vediamo come si calcola l’equazione ordinaria di una circonferenza con un esempio:

Determinare l’equazione ordinaria della circonferenza di raggio 5 il cui centro è il punto
$C(3,-1).$

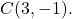
La formula per l’equazione ordinaria di una circonferenza è:

$(x-a)^2+(y-b)^2=r^2$

Pertanto, dobbiamo solo sostituire l’ignoto

$r$

dal valore del raggio e dalle incognite

$a$

$b$

dalle coordinate X e Y rispettivamente del centro della circonferenza:

$(x-3)^2+(y-(-1))^2=5^2$

Quindi l’equazione ordinaria della circonferenza è:

$\bm{(x-3)^2+(y+1)^2=25}$

Equazione generale della circonferenza

Un altro tipo di equazione della circonferenza è l’equazione generale, infatti è la più utilizzata. Vedremo poi come ottenere l’equazione generale di una circonferenza qualunque dalla sua equazione ordinaria.

Consideriamo l’equazione ordinaria di una circonferenza:

$(x-a)^2+(y-b)^2=r^2$

Se sviluppiamo le uguaglianze notevoli (o i prodotti notevoli):

$x^2+a^2-2ax+y^2+b^2-2by=r^2$

$x^2-2ax+y^2-2by+a^2+b^2-r^2=0$

Ora effettuiamo 3 cambi di variabili:

$A=-2a \qquad B=-2b \qquad C=a^2+b^2-r^2$

Ed infine otteniamo l’equazione generale della circonferenza:

$x^2+y^2+Ax+By+C=0$

La formula per l’ equazione generale della circonferenza è quindi:

$x^2+y^2+Ax+By+C=0$

dove il centro del cerchio è:

$\displaystyle C\left(-\frac{A}{2}, -\frac{B}{2}\right)$

E il raggio del cerchio è:

$\displaystyle r=\sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C}$

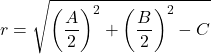
Quindi questa equazione della circonferenza si ottiene sempre con l’equazione ordinaria. Ecco un esempio per vedere come è fatto:

Determinare l’equazione generale della circonferenza di raggio 6 il cui centro è il punto
$C(2,4).$

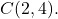
Per prima cosa dobbiamo trovare l’equazione ordinaria della circonferenza. Per fare questo, usiamo la sua formula:

$(x-a)^2+(y-b)^2=r^2$

$(x-2)^2+(y-4)^2=6^2$

Ed ora operiamo finché non troviamo l’equazione generale della circonferenza, vale a dire finché non possiamo più semplificare:

$x^2+2^2-2\cdot x \cdot 2+y^2+4^2-2\cdot y \cdot 4=36$

$x^2+4-4x+y^2+16-8y=36$

$x^2-4x+y^2-8y+4+16-36=0$

$x^2-4x+y^2-8y-16=0$

Quindi l’equazione generale della circonferenza è:

$\bm{x^2+y^2-4x-8y-16=0}$

Sebbene il problema non lo richiedesse, ora possiamo calcolare il centro e il raggio dell’equazione trovata per verificare che sia corretta.

Per determinare il centro del cerchio, usiamo la sua formula:

$\displaystyle C\left(-\frac{A}{2}, -\frac{B}{2}\right)$

$\displaystyle C\left(-\frac{-4}{2}, -\frac{-8}{2}\right)$

$\displaystyle C\bigl(-(-2), -(-4)\bigr)$

$\displaystyle C\left(2,4\right)$

Infatti il centro del cerchio coincide con quello dell’enunciato.

Controlliamo anche il raggio della circonferenza con la sua formula:

$\displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{-4}{2}\right)^2 +\left(\frac{-8}{2}\right)^2-(-16)} \\[2ex] & =\sqrt{\left(-2\right)^2 +\left(-4\right)^2+16} \\[2ex] &= \sqrt{4+16+16} \\[2ex] &= \sqrt{36} \\[2ex] & = 6 \end{aligned}$

E anche il raggio è uguale a quello dell’enunciato. Pertanto, l’equazione della circonferenza calcolata è corretta.

Esistenza di una circonferenza

Tutte le equazioni nella forma di

$x^2+y^2+Ax+By+C=0$

corrispondono ad un cerchio. Pertanto, affinché questo tipo di espressione sia veramente l’equazione di un cerchio, devono essere soddisfatte le seguenti 3 condizioni:

I coefficienti di
$x^2$

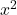
e di

$y^2$

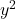
devono essere uguali a 1. Tieni presente che se entrambe le variabili fossero precedute da un numero diverso da uno ma avessero entrambe lo stesso numero, l’intera equazione potrebbe essere divisa per quel numero in modo che i loro coefficienti siano 1.
L’equazione non può avere un termine
$xy.$
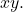
La seguente espressione deve essere positiva:

Le due equazioni della circonferenza che abbiamo visto, l’equazione ordinaria e l’equazione generale, sono le più utilizzate per esprimere matematicamente una circonferenza nel piano (in R2). Tuttavia, esistono diversi tipi di equazioni per descrivere questo oggetto geometrico, di seguito è riportata la spiegazione di ciascuna di esse.

Equazione canonica della circonferenza

L’equazione canonica, o equazione ridotta, di una circonferenza si usa per descrivere qualsiasi circonferenza il cui centro si trova nell’origine delle coordinate , cioè nel punto (0,0). Detta equazione è la seguente:

$x^2+y^2=r^2$

Se inoltre il raggio fosse equivalente all’unità (1), l’equazione della circonferenza sarebbe:

$x^2+y^2=1$

Quest’ultima equazione corrisponde alla circonferenza goniometrica, detta anche circonferenza unitaria o cerchio unitario. È il cerchio di raggio 1 centrato nell’origine delle coordinate.

Equazioni di due cerchi concentrici

Due equazioni concentriche sono quelle che hanno il centro nello stesso punto. E l’unica cosa diversa che hanno due cerchi concentrici è il raggio.

Quindi affinché questa condizione sia soddisfatta, le equazioni di due cerchi concentrici sono esattamente le stesse tranne che per i loro termini indipendenti, che devono essere diversi.

$x^2+y^2+Ax+By+C=0$

$x^2+y^2+Ax+By+C'=0$

Ad esempio, i seguenti due cerchi sono concentrici, poiché tutti i loro coefficienti sono identici tranne i termini indipendenti:

$x^2+y^2+3x-4y+1=0$

$x^2+y^2+3x-4y+5=0$

Equazione parametrica della circonferenza

Come la retta, anche l’equazione della circonferenza può essere parametrizzata con le funzioni trigonometriche seno e coseno. Pertanto le equazioni parametriche della circonferenza sono:

$\diplaystyle \begin{cases}x= a + r \cdot \text{cos}(t) \\[2ex] y= b + r\cdot \text{sen}(t)\end{cases} \qquad t\in[0,2\pi)$

dov’è il punto

$(a,b)$

è il centro del cerchio e

$r$

Questo è il tuo dipartimento.

Problemi risolti dell’equazione della circonferenza

Esercizio 1

Calcola l’equazione generale della circonferenza di raggio 5 il cui centro è nel punto

$C(-1,2).$

vedi soluzione

Per trovare l’equazione generale della circonferenza dobbiamo prima trovare la sua equazione ordinaria. Per fare ciò, usiamo la formula per l’equazione ordinaria di una circonferenza:

$(x-a)^2+(y-b)^2=r^2$

$(x-(-1))^2+(y-2)^2=5^2$

$(x+1)^2+(y-2)^2=25$

Una volta conosciuta l’equazione ordinaria, lavoriamo finché non troviamo l’equazione generale della circonferenza:

$x^2+1^2+2\cdot x \cdot 1+y^2+2^2-2\cdot y \cdot 2=25$

$x^2+1+2x+y^2+4-4y=25$

$x^2+2x+y^2-4y+1+4-25=0$

$x^2+2x+y^2-4y-20=0$

Quindi l’equazione generale della circonferenza è:

$\bm{x^2+y^2+2x-4y-20=0}$

Esercizio 2

Per ciascuno dei seguenti cerchi, trova le coordinate del suo centro e la lunghezza del suo raggio.

$\text{A)}\ (x-2)^2+(y+5)^2=36$

$\text{B)}\ x^2+y^2+8x-10y+1 = 0$

$\text{C)}\ x^2+y^2=4$

vedi soluzione

circonferenza A)

$(x-2)^2+(y+5)^2=36$

La circonferenza è espressa sotto forma di un’equazione ordinaria, la cui formula è:

$(x-a)^2+(y-b)^2=r^2$

Pertanto le coordinate del centro del cerchio sono:

$C(a,b)$

$\bm{C(2,-5)}$

E il suo raggio è:

$r^2=36$

$\bm{r=6}$

circonferenza B)

$x^2+y^2+8x-10y+1 = 0$

Questa circonferenza è espressa sotto forma di un’equazione generale, quindi per calcolare le coordinate del suo centro è necessario utilizzare la seguente formula:

$\displaystyle C\left(-\frac{A}{2}, -\frac{B}{2}\right)$

$\displaystyle C\left(-\frac{8}{2}, -\frac{-10}{2}\right)$

$\displaystyle C\bigl(-4, -(-5)\bigr)$

$\displaystyle \bm{C(-4, 5)}$

La formula per trovare il raggio del cerchio invece è:

$\displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{8}{2}\right)^2 +\left(\frac{-10}{2}\right)^2-1} \\[2ex] & =\sqrt{\left(4\right)^2 +\left(-5\right)^2-1} \\[2ex] &= \sqrt{16+25-1} \\[2ex] &= \bm{\sqrt{40}} \end{aligned}$

circonferenza C)

$x^2+y^2=4$

La circonferenza è espressa sotto forma di un’equazione ordinaria, la cui formula è:

$(x-a)^2+(y-b)^2=r^2$

Pertanto le coordinate del centro del cerchio sono:

$C(a,b)$

In questo caso l’equazione non ha termini.

$a$

nessuno dei due

$b,$

è quindi centrato sull’origine delle coordinate:

$\bm{C(0,0)}$

E il suo raggio è:

$r^2=4$

$\bm{r=2}$

Esercizio 3

Quale delle seguenti equazioni è l’equazione di una circonferenza?

$\text{A)}\ x^2+y^2+4x-6y-1=0$

$\text{B)}\ x^2+y^2+5x+5y+2xy-4 = 0$

$\text{C)}\ 2x^2+2y^2-8x+4y+2=0$

$\text{D)}\ x^2+y^2+x+2y+6=0$

vedi soluzione

Affinché un’espressione sia l’equazione di una circonferenza, devono essere vere le seguenti condizioni:

1. I coefficienti di

$x^2$

e di

$y^2$

Devono essere uguali a 1.
2. L’equazione non può avere un termine

$xy.$

Equazione A)

$x^2+y^2+4x-6y-1=0$

I coefficienti di

$x^2$

$y^2$

sono 1 e l’equazione non ha termini

$xy.$

Basta quindi verificare la terza condizione:

$\displaystyle \left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-C>0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”190″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”216″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”22″ width=”146″ style=”vertical-align: -5px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”103″ style=”vertical-align: -2px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”49″ style=”vertical-align: -2px;”> <p class=$ 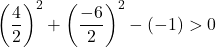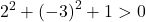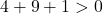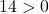L’equazione soddisfa le 3 condizioni, quindi è l’equazione di una circonferenza.

Equazione B)

$x^2+y^2+5x+5y+2xy-4 = 0$

L’equazione ha un termine con

$xy,$

con cui l’equazione non corrisponde ad un cerchio.

Equazione C)

$2x^2+2y^2-8x+4y+2=0$

I coefficienti di

$x^2$

$y^2$

non sono 1, ma possiamo trasformare l’equazione dividendo tutti i termini:

$x^2+y^2-4x+2y+1=0$

In questo modo ora i coefficienti di

$x^2$

$y^2$

sì, sono 1 e, inoltre, l’equazione non ha termini

$xy.$

Non ci resta quindi che corroborare la terza condizione:

$\displaystyle \left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-C>0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”190″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”189″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”22″ width=”158″ style=”vertical-align: -5px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”103″ style=”vertical-align: -2px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”42″ style=”vertical-align: -2px;”> <p class=$ 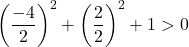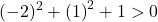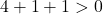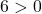L’equazione soddisfa le 3 condizioni, quindi è l’equazione di una circonferenza.

Equazione D)

$x^2+y^2+x+2y+6=0$

I coefficienti di

$x^2$

$y^2$

sono 1 e l’equazione non ha termini

$xy.$

Basta quindi verificare la terza condizione:

$\displaystyle \left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-C>0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”190″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”175″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”17″ width=”128″ style=”vertical-align: -4px;”> } \ 0″ title=”Rendered by QuickLaTeX.com” height=”17″ width=”82″ style=”vertical-align: -4px;”> <p class=$ 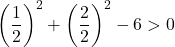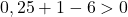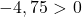L’equazione non soddisfa l’ultima condizione, quindi non è l’equazione di una circonferenza .

Esercizio 4

Determina l’equazione della circonferenza passante per i seguenti tre punti:

$A(0,0) \quad B(3,0) \quad C(2,-2)$

vedi soluzione

L’equazione generale di ogni circonferenza è:

$x^2+y^2+Ax+By+C=0$

Pertanto, dobbiamo sostituire le coordinate dei punti nell’equazione del cerchio per trovare i parametri

$A,$

$B$

$C.$

Con il primo punto troviamo il coefficiente

$C:$

$A(0,0) \ \longrightarrow \ 0^2+0^2+A\cdot 0 +B\cdot 0+C=0 \ \longrightarrow \ \bm{C = 0}$

Con il secondo punto troviamo il coefficiente

$A:$

$\begin{aligned}A(3,0) \ \longrightarrow \ & 3^2+0^2+A\cdot 3 +B\cdot 0+C=0 \\[2ex] & 9+A\cdot 3 =0\\[2ex]& \bm{A=-3} & \end{aligned}$

E dal terzo punto troviamo il coefficiente

$B:$

$\begin{aligned} A(2,-2) \ \longrightarrow \ & 2^2+(-2)^2+A\cdot 2 +B\cdot (-2)+C=0 \\[2ex] & 4+4+(-3)\cdot 2+ B\cdot (-2)+0=0 \\[2ex] & 8-6-2B=0 \\[2ex] & \bm{B=1} \end{aligned}$

In conclusione, l’equazione generale della circonferenza è:

$\bm{x^2+y^2-3x+y=0}$

Esercizio 5

Se gli estremi opposti di un cerchio sono i seguenti due punti:

$A(2,3) \qquad B(6,-1)$

Qual è l’equazione ordinaria della circonferenza?

vedi soluzione

Se i due punti sono gli estremi del cerchio, il suo centro sarà il punto medio tra questi due punti:

$\displaystyle C\left(\frac{2+6}{2} , \frac{3+(-1)}{2} \right)$

$\displaystyle C\left(\frac{8}{2} , \frac{2}{2} \right)$

$\displaystyle C\left(4,1 \right)$

Il diametro del cerchio sarà invece la distanza tra i due punti, che può essere calcolata utilizzando il modulo del vettore che formano i due punti:

$\vv{AB} = B-A=(6,-1) - (2,3) = (4,-4)$

$d = \lvert \vv{AB} \rvert =\sqrt{4^2+(-4)^2} = \sqrt{16+16} = \sqrt{32}$

E il raggio del cerchio è la metà del diametro:

$r = \cfrac{\sqrt{32}}{2}$

L’equazione ordinaria della circonferenza è quindi:

$(x-a)^2+(y-b)^2=r^2$

$\displaystyle (x-4)^2+(y-1)^2=\left(\frac{\sqrt{32}}{2}\right)^2$

$\displaystyle \bm{(x-4)^2+(y-1)^2=}\frac{\bm{32}}{\bm{4}}$

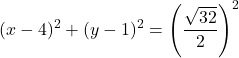
Infine, se questo articolo ti è stato utile, sicuramente ti interesseranno anche le nostre pagine sull’iperbole (matematica) e sulla parabola (matematica) . Troverai una spiegazione dettagliata di cosa sono l’iperbole e la parabola, le loro equazioni, le loro caratteristiche, esempi, esercizi risolti…

Equazione ordinaria della circonferenza

Equazione generale della circonferenza

Esistenza di una circonferenza

Equazione canonica della circonferenza

Equazioni di due cerchi concentrici

Equazione parametrica della circonferenza

Problemi risolti dell’equazione della circonferenza

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Lascia un commento Annulla risposta