Trasformazioni di funzioni: Traslazione, Espansione e Simmetria

Questa pagina spiega cosa sono le trasformazioni di funzioni e come trovarle. Esistono tre tipi di trasformazioni: traslazioni (o spostamenti), simmetrie ed espansioni (o contrazioni). Troverai anche esercizi risolti passo dopo passo così potrai esercitarti e comprendere i concetti senza lasciare dubbi.

Cosa sono le trasformazioni di funzioni?

A volte ci può essere chiesto di rappresentare graficamente funzioni elementari molto simili ad altre che già conosciamo. Ebbene, invece di rappresentare nuovamente la funzione simile, è possibile utilizzare delle tecniche per passare dalla rappresentazione di una funzione a un’altra in modo semplice e rapido.

Le trasformazioni di funzioni sono quindi tecniche che permettono di passare dalla rappresentazione grafica di una funzione alla rappresentazione grafica di un’altra funzione molto simile attraverso operazioni elementari.

Fondamentalmente esistono tre tipi di trasformazioni di funzioni elementari:

Traslazioni o movimenti : una funzione può essere spostata verticalmente e orizzontalmente.
Riflessioni o simmetrie : una funzione può essere riflessa utilizzando l’asse X o l’asse Y come asse di simmetria.
Espansioni e compressioni : una funzione può essere ingrandita o ridotta.

Una volta compreso il concetto di trasformazione di una funzione, approfondiremo ogni tipo di modifica.

Traslazioni o spostamenti di funzioni

Inizieremo con i turni di funzione. Ne esistono di due tipi: traslazioni verticali e traslazioni orizzontali.

Traslazione o movimento verticale di una funzione

Per traslare o spostare una funzione verticalmente (lungo l’asse Y), è necessario aggiungere o sottrarre una costante alla funzione:

Spostiamo una funzione di k unità verso l’alto aggiungendo ka alla funzione:

$\bm{f(x)+k}$

Spostiamo una funzione di k unità verso il basso sottraendo ka dalla funzione:

$\bm{f(x)-k}$

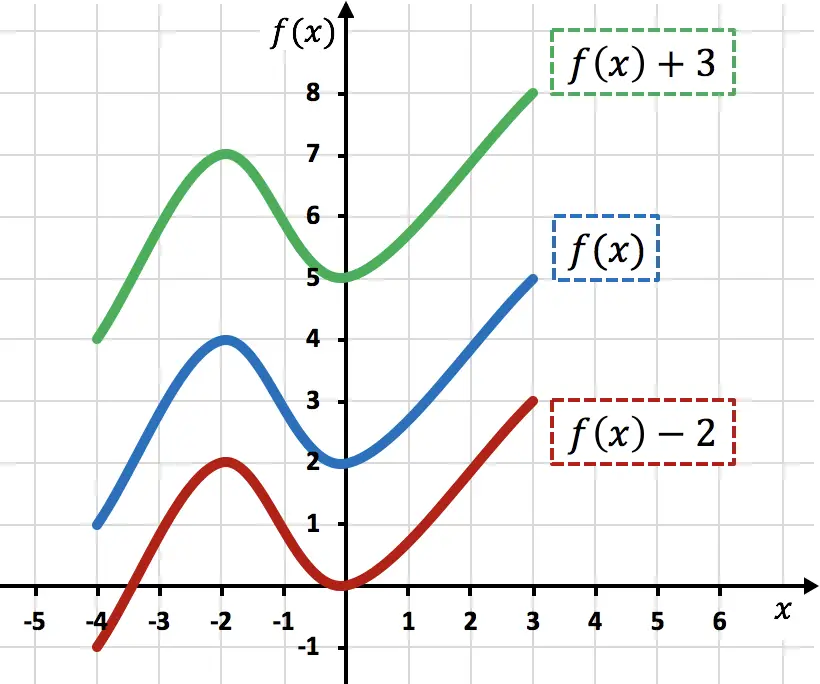
Traslazione o movimento verticale di una funzione

Come puoi vedere dal grafico, l’aggiunta di una costante a qualsiasi funzione sposta le unità aggiunte verso l’alto (funzione verde). Quando invece si sottrae un numero da una funzione, le unità sottratte vengono spostate verso il basso (funzione rossa).

Si noti che in questo tipo di movimenti vengono modificate solo le coordinate Y dei punti funzione, mentre le coordinate X rimangono le stesse.

Traslazione o spostamento orizzontale delle funzioni

Per traslare o spostare una funzione orizzontalmente (lungo l’asse X) è necessario aggiungere o sottrarre una costante alla variabile indipendente x :

Il grafico di

$\bm{f(x+k)}$

è il grafico di

$f(x)$

spostato k unità a sinistra.

Il grafico di

$\bm{f(x-k)}$

è il grafico di

$f(x)$

spostato k unità a destra.

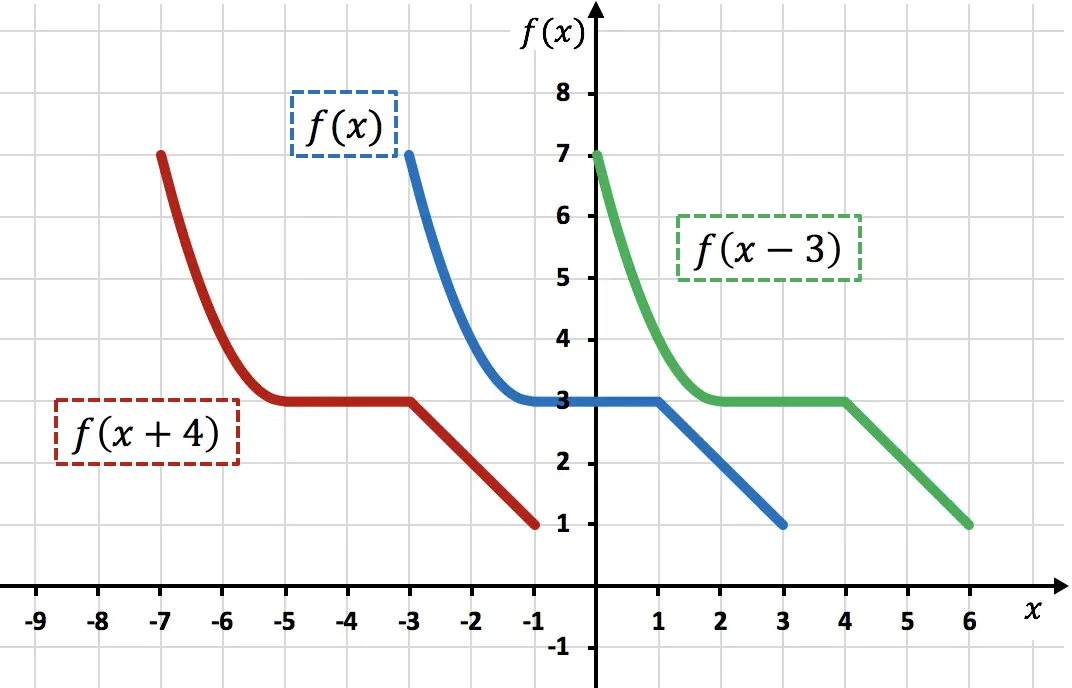
Traslazione o movimento orizzontale di una funzione

Come puoi vedere dal grafico, quando si aggiunge una costante direttamente alla variabile x , la funzione sposta le unità aggiunte a sinistra (funzione rossa). D’altra parte, quando si sottrae un numero dalla variabile x , la funzione sposta le unità sottratte verso destra (funzione verde).

Si noti che in questo tipo di movimenti vengono modificate solo le coordinate X dei punti funzione, mentre le coordinate Y continuano con lo stesso valore.

Esempio di traslazione o spostamento di una funzione

Sposta la seguente funzione di 4 unità in alto e di 3 unità a destra:

$f(x)=x^2$

Per spostare la funzione verso l’alto di 4 unità, dobbiamo aggiungere 4 unità alla funzione:

$f(x) + 4 = x^2 + 4$

E anche per spostare la funzione di 3 unità a destra dobbiamo calcolare

$f(x-3)$

. Pertanto, dove c’è a

$x$

noi possiamo

$x-3 :$

$f(x-3) = (x-3)^2 + 4$

La funzione spostata di 4 unità in alto e di 3 unità a destra è quindi:

$\bm{f(x) = (x-3)^2 + 4}$

Di seguito sono rappresentate graficamente la funzione originale e la funzione trasformata in modo da poter vedere la differenza tra loro:

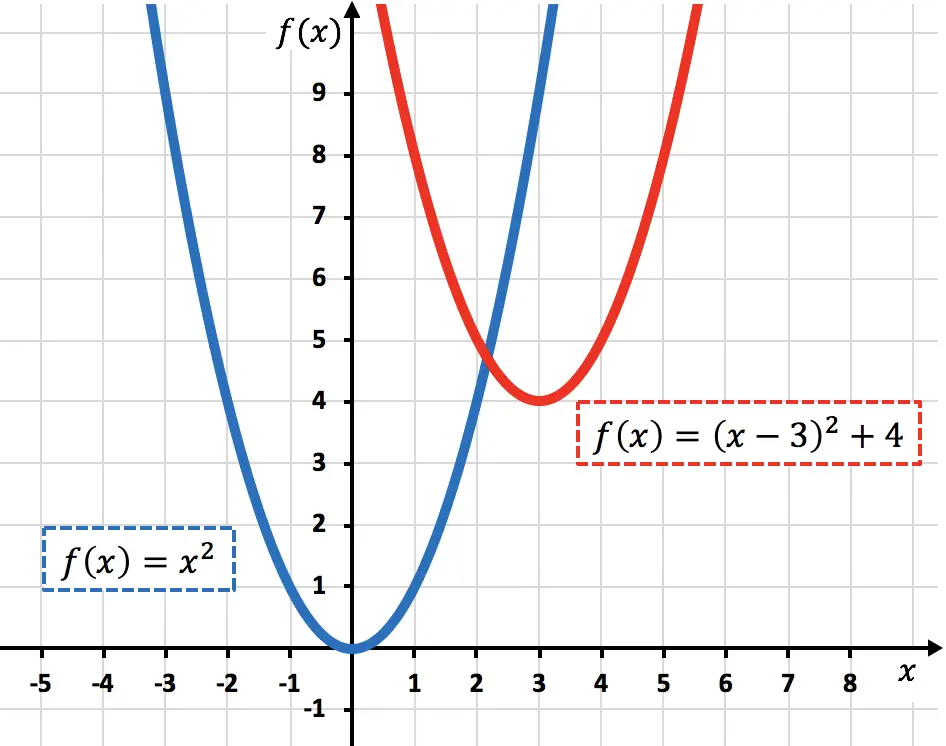
esempio di traslazione o movimento di una funzione

Alcuni matematici chiamano spostamento obliquo o traslazione quando entrambi i tipi di movimento si verificano contemporaneamente.

Riflessione o simmetria di una funzione rispetto agli assi coordinati

Possiamo rappresentare la funzione simmetrica rispetto a un qualsiasi asse cartesiano nel modo seguente:

Per riflettere una funzione rispetto all’asse x, dobbiamo cambiare il segno della funzione, cioè dobbiamo calcolare

$\bm{-f(x)}.$

Per riflettere una funzione rispetto all’asse y, dobbiamo negare la variabile indipendente x , cioè dobbiamo calcolare

$\bm{f(-x)}.$

riflessione o simmetria rispetto all'asse X

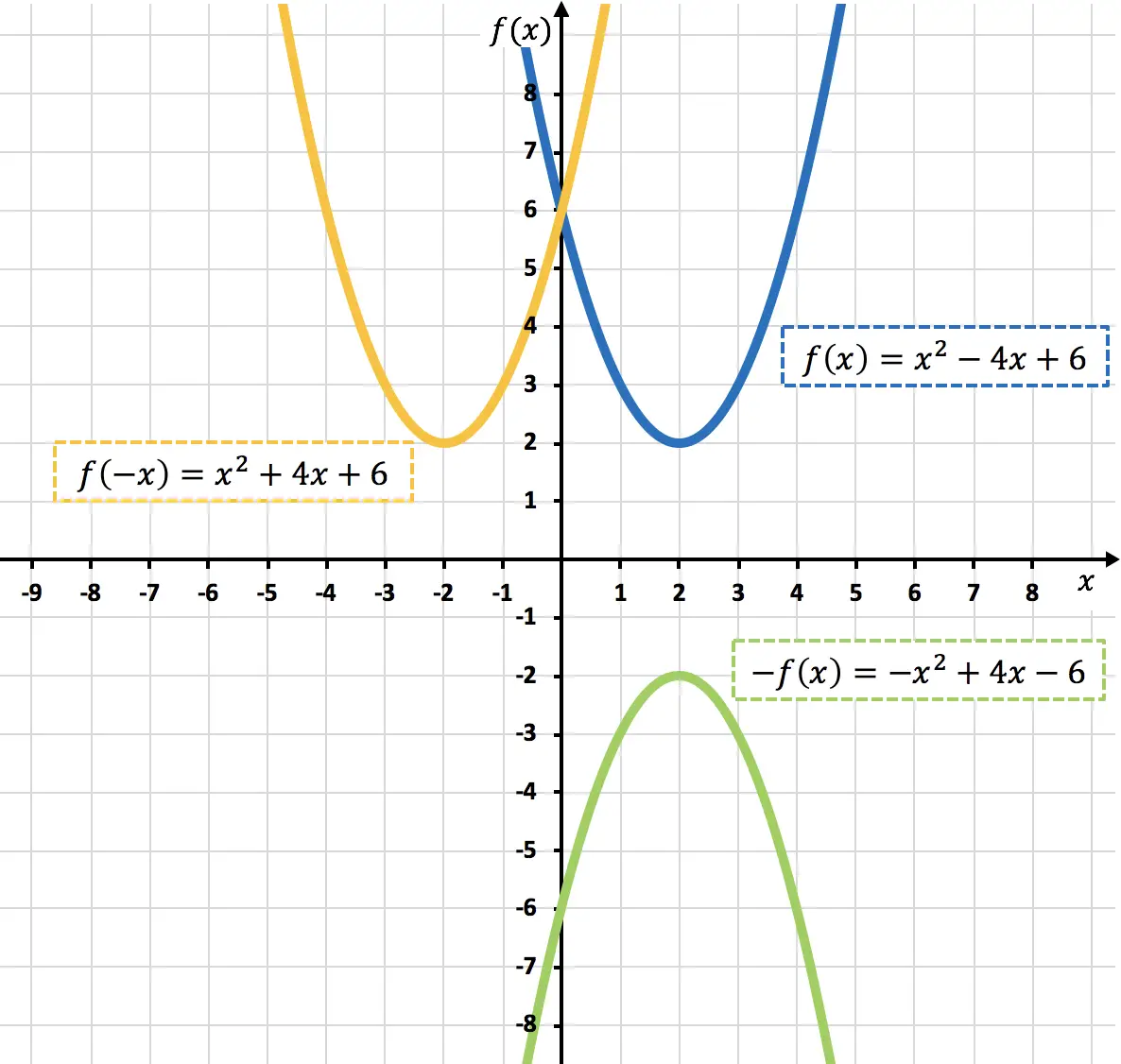
Come puoi vedere nel grafico precedente, moltiplicando una funzione per -1, la invertiamo graficamente (funzione arancione), o in altre parole la specchiamo rispetto all’asse X.

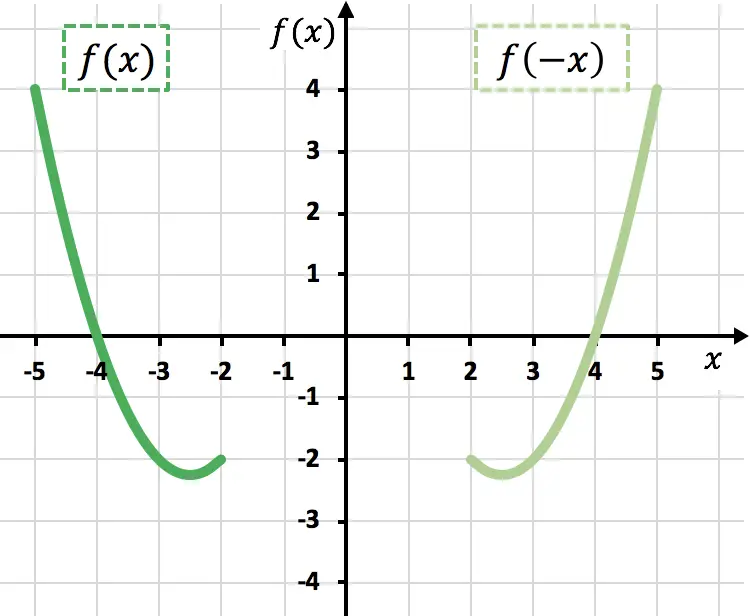
riflessione o simmetria attorno all'asse Y

Come si può vedere nel grafico precedente, negando la variabile x si specchia la funzione rispetto all’asse Y (funzione verde chiaro).

Esempio di mirroring di una funzione

Calcola la funzione simmetrica rispetto all’asse OX e la funzione simmetrica rispetto all’asse OY della seguente funzione quadratica:

$f(x)=x^2-4x+6$

Per trovare la funzione simmetrica rispetto all’asse X, dobbiamo fare

$-f(x)$

$-f(x)=-\bigl[x^2-4x+6\bigr]$

$\bm{-f(x)=-x^2+4x-6}$

E per trovare la funzione simmetrica rispetto all’asse Y dobbiamo farlo

$f(-x)$

. Pertanto, sostituiamo dove c’è a

$x$

nella funzione originale dal termine

$-x :$

$f(x)=x^2-4x+6$

$f(-x)=(-x)^2-4\cdot (-x)+6$

$f(-x)=x^2-4\cdot (-x)+6$

$\bm{f(-x)=x^2+4x+6}$

Di seguito hai rappresentato sia la funzione originale che le funzioni simmetriche trovate:

esempio di funzioni simmetriche rispetto agli assi xey

Espansioni e contrazioni di funzioni

Come per le traduzioni, ci sono due tipi di espansioni o contrazioni: verticale e orizzontale.

Espansione e contrazione verticale di una funzione

Moltiplicando una funzione intera per un coefficiente, possiamo farla espandere o contrarre:

Per espandere (o dilatare) una funzione sull’asse Y, dobbiamo moltiplicarla per un numero maggiore di 1:

$kf(x)\qquad k>1″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”121″ style=”vertical-align: -5px;”></p> </p> <p style=$ Per ridurre una funzione sull’asse Y, dobbiamo moltiplicarla per un numero positivo inferiore a 1:

$kf(x)\qquad 0</div> <div class="wp-block-image"> <figure class="aligncenter size-large is-resized"><img decoding="async" loading="lazy" src="http://mathority.org/wp-content/uploads/2023/07/expansion-et-contraction-d-une-fonction.webp" alt="expansion et contraction verticales d'une fonction" class="wp-image-320" width="442" height="438" srcset="" sizes="" data-src=""></figure> </div> <p> Comme vous pouvez le voir dans le graphique précédent, si on multiplie une fonction par un coefficient supérieur à 1 (fonction verte) on la rend plus grande le long de l’axe OY, en revanche, si on multiplie une fonction par un coefficient supérieur à 0 mais plus petit que 1 (fonction rouge), nous le rendons plus petit le long de l’axe OY.</p> <h3 class="wp-block-heading"> Expansion et contraction horizontales d’une fonction</h3> <p> Dans ce cas, au lieu de multiplier la fonction entière par un coefficient, pour qu’une fonction se dilate ou se contracte horizontalement, nous devons multiplier la variable indépendante <em>x</em> . </p> <div style="padding-top: 23px; padding-bottom: 0.5px; padding-right: 30px; padding-left: 30px; border: 2px dashed #FF9B28; border-radius:20px;"> Pour <strong>étendre (ou dilater) une fonction sur l’axe X,</strong> il faut multiplier tous les <em>x</em> par un nombre compris entre 0 et 1 :” title=”Rendered by QuickLaTeX.com” height=”392″ width=”2425″ style=”vertical-align: -4px;”></p> <p> f(kx)\qquad 0</p> <p style=$ Per ridurre una funzione sull’asse X, dobbiamo moltiplicare tutte le x per un numero maggiore di 1:

$f(kx)\qquad k>1″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”121″ style=”vertical-align: -5px;”></p> </p> </div> <div class=$

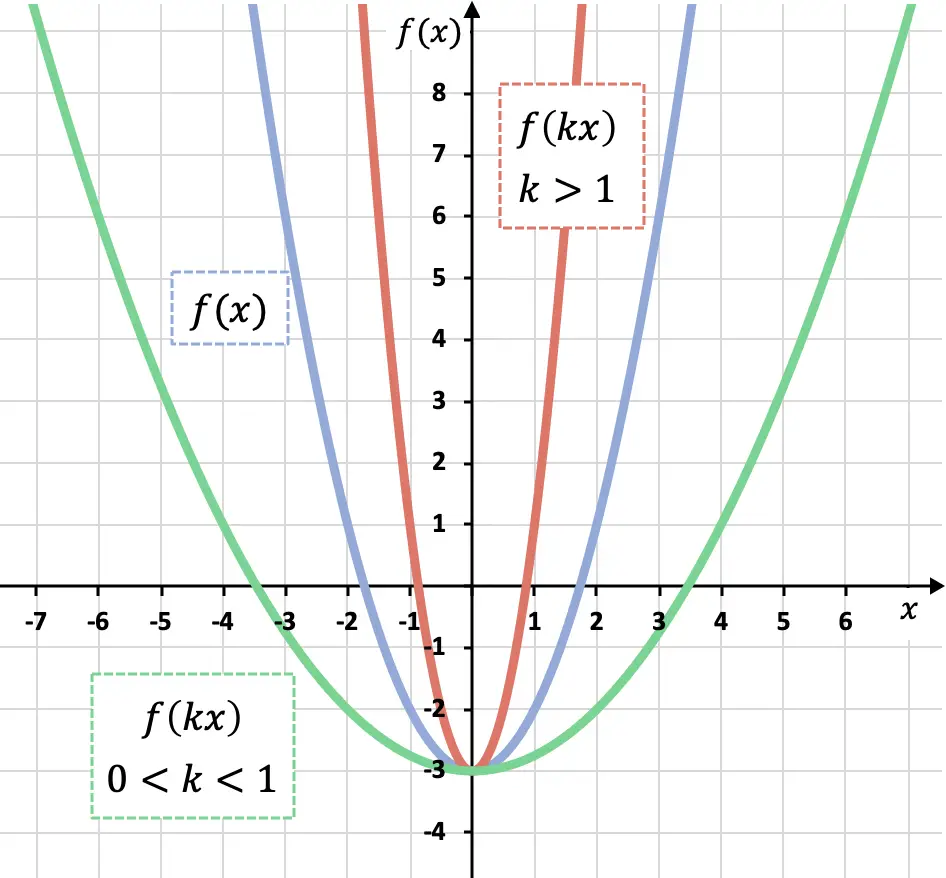
espansione o contrazione orizzontale di una funzione

Come puoi vedere nel grafico precedente, se moltiplichiamo tutte le x di una funzione per un coefficiente maggiore di 0 ma minore di 1 (funzione verde) la allarghiamo lungo l’asse OX, se invece moltiplichiamo una funzione per un coefficiente maggiore di 1 (funzione rossa) la riduciamo lungo l’asse OX.

Esempio di come espandere o comprimere una funzione

Duplica verticalmente e orizzontalmente la seguente funzione irrazionale:

$f(x)=\sqrt{9-x^2}$

Per estendere per due la funzione sull’asse y, dobbiamo moltiplicare l’intera funzione per 2:

$2f(x)=2\sqrt{9-x^2}$

E per espandere la funzione anche per due sull’asse x, dobbiamo moltiplicare tutte le x della funzione per

$\displaystyle \frac{1}{2}:$

$\displaystyle f\left(\frac{1}{2}x\right)=2\sqrt{9-\left(\frac{1}{2}x\right)^2}$

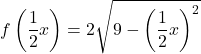
La funzione duplicata sui due assi coordinati è quindi:

$\displaystyle\bm{f(x) = 2\sqrt{9-\left(\frac{1}{2}x\right)^2}}$

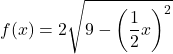
Di seguito hai rappresentato graficamente la funzione originale e quella trasformata in modo da poter vedere le differenze tra loro:

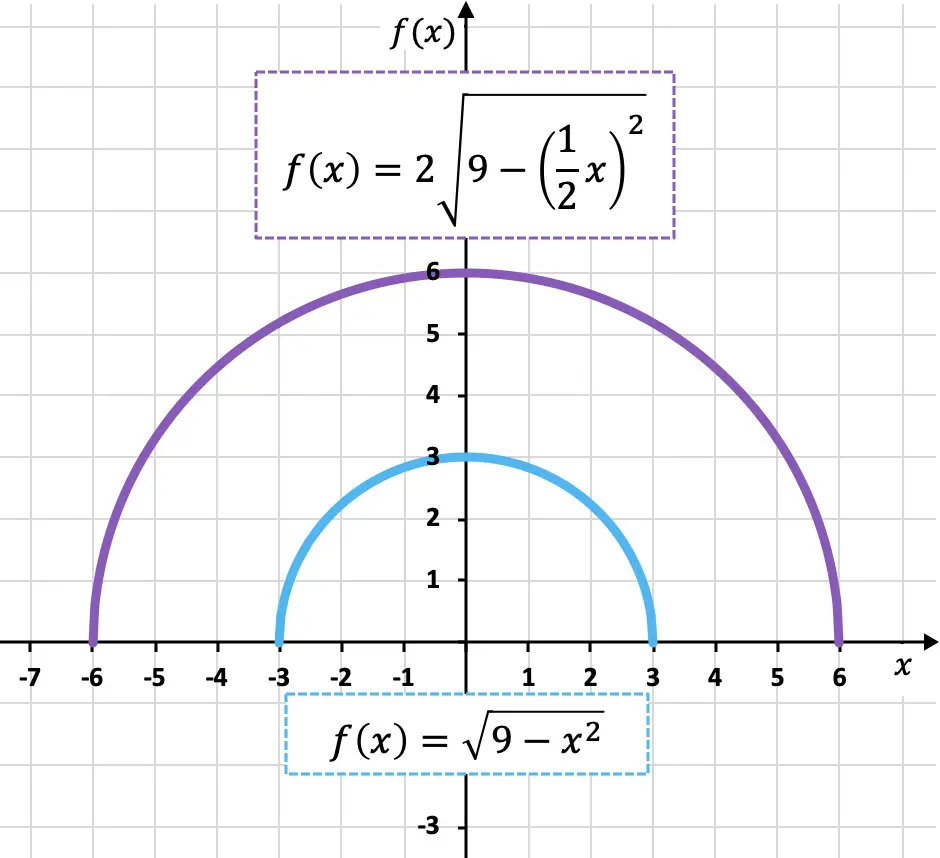
esempio di come espandere e comprimere una funzione

Come puoi vedere, la nuova funzionalità (colore viola) è due volte più grande della funzionalità originale (colore blu) sia verticalmente che orizzontalmente, pertanto la funzionalità si è espansa.

Esercizi risolti sulle trasformazioni di funzioni

Esercizio 1

Sposta la seguente funzione di terzo grado verso l’alto di 5 unità:

$f(x) = 4x^3-9x-2$

Vedi la soluzione

Per spostare la funzione su 5 unità, aggiungi 5 alla funzione:

$\begin{aligned} f(x) + 5 & = 4x^3-9x-2 + 5 \\[2ex] & = 4x^3-9x+3 \end{aligned}$

La funzione spostata di 5 unità è quindi:

$\bm{f(x) = 4x^3-9x+3}$

Esercizio 2

Trova la funzione simmetrica attorno all’asse Y della seguente funzione quadratica:

$f(x) = 2x^2-3x+6$

Vedi la soluzione

Per trovare la funzione simmetrica rispetto all’asse Y è necessario calcolare

$f(-x)$

, cioè dobbiamo sostituire

$x$

Per

$-x$

nella funzione:

$f(-x) = 2(-x)^2-3\cdot (-x)+6$

$f(-x) = 2x^2+3x+6$

La funzione simmetrica rispetto all’asse OY è quindi:

$\bm{f(x) = 2x^2+3x+6}$

Esercizio 3

Esegui una compressione orizzontale della seguente funzione a un terzo della sua rappresentazione:

$f(x) = x^3-4x^2-5x+1$

Vedi la soluzione

Per ridurre una funzione attraverso il

$f(3x) = (3x)^3-4(3x)^2-5(3x)+1$

$f(3x) = 27x^3-4\cdot 9 x^2-15x+1$

$f(3x) = 27x^3-36 x^2-15x+1$

La funzione ridotta è quindi:

$\bm{f(x) = 27x^3-36 x^2-15x+1}$

Esercizio 4

Calcola la funzione simmetrica rispetto all’asse OX della seguente funzione traslata di 4 unità a destra:

$f(x) = 3x^3-x^2+5x+8$

Vedi la soluzione

Prima di calcolare la funzione simmetrica dobbiamo prima spostare la funzione di 4 unità verso destra, quindi:

$f(x-4) = 3(x-4)^3-(x-4)^2+5(x-4)+8$

$f(x-4) = 3(x-4)^3-(x-4)^2+5x-20+8$

$f(x-4) = 3(x-4)^3-(x-4)^2+5x-12$

E una volta spostata la funzione, calcoliamo la funzione simmetrica rispetto all’asse X. Per fare ciò dobbiamo negare la funzione ottenuta:

$\displaystyle -f(x) = -\Bigl[3(x-4)^3-(x-4)^2+5x-12\Bigr]$

$-f(x) = -3(x-4)^3+(x-4)^2-5x+12$

In breve la funzione dopo aver applicato tutte le operazioni elementari è:

$\bm{f(x) =-3(x-4)^3+(x-4)^2-5x+12}$

Esercizio 5

Sposta la seguente funzione di 2 unità a sinistra, quindi espandila verticalmente di un fattore 4:

$f(x) = x^4-5x^3-x-3$

Vedi la soluzione

Per prima cosa spostiamo la funzione di due unità a sinistra:

$f(x+2) = (x+2)^4-5(x+2)^3-(x+2)-3$

$f(x-4) = (x+2)^4-5(x+2)^3-x-2-3$

$f(x-4) = (x+2)^4-5(x+2)^3-x-5$

E poi espandiamo la funzione lungo l’asse Y con un fattore 4:

$4\cdot f(x) = 4\cdot \Bigl[(x+2)^4-5(x+2)^3-x-5\Bigr]$

$f(x) = 4(x+2)^4-20(x+2)^3-4x-20$

In conclusione, la funzione dopo aver applicato tutte le trasformazioni elementari è:

$\bm{f(x) =4(x+2)^4-20(x+2)^3-4x-20}$

Esercizio 6

Dalla funzione

$f(x)=x,$

determinare quale delle rappresentazioni sul grafico corrisponde alla funzione

$f(x)=x-3 .$

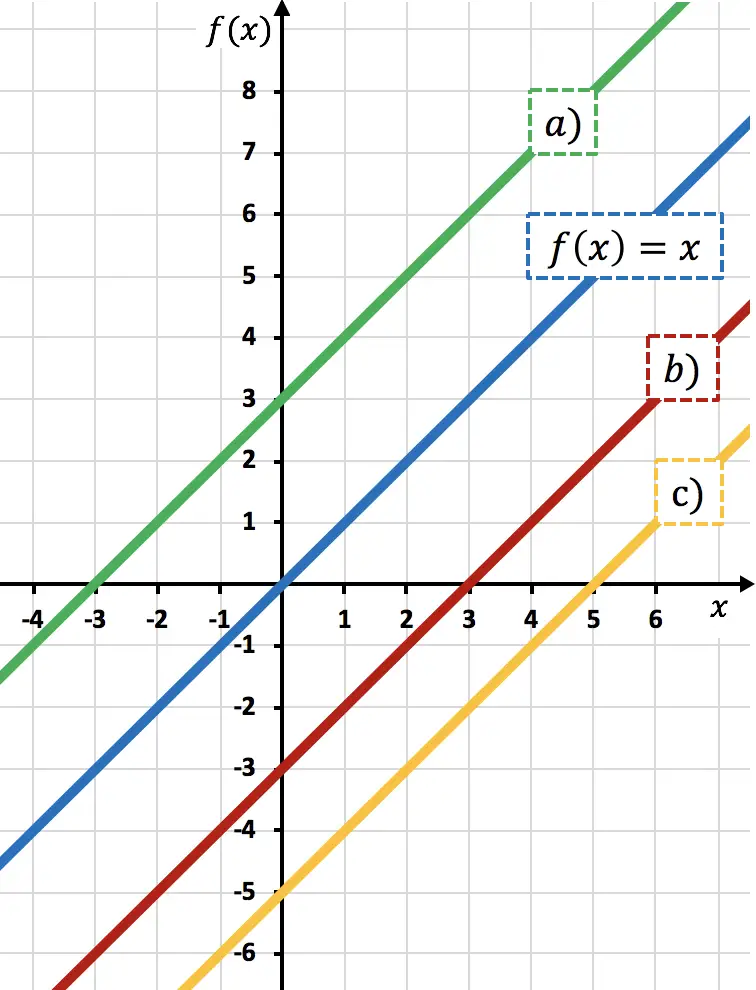
esercizi risolti passo passo sulle trasformazioni di funzioni

Vedi la soluzione

Funzione

$f(x)=x-3$

è la funzione

$f(x)=x$

spostato di 3 unità verso il basso. Perché sottraendo un numero da una funzione, sposti la funzione verso il basso.

Pertanto, la rappresentazione di

$f(x)=x-3$

corrisponde alla linea b) , perché è spostata di 3 unità verso il basso rispetto a

$f(x)=x .$

Questo può essere visto guardando l’asse verticale: quando

$f(x)=x$

passa per 0, la linea rossa passa per -3, quindi viene spostata di 3 unità verso il basso.

Esercizio 7

Dalla funzione

$f(x)=x^2+2,$

determinare quale parabola è la rappresentazione della funzione

$f(x)=(x-6)^2+2 .$

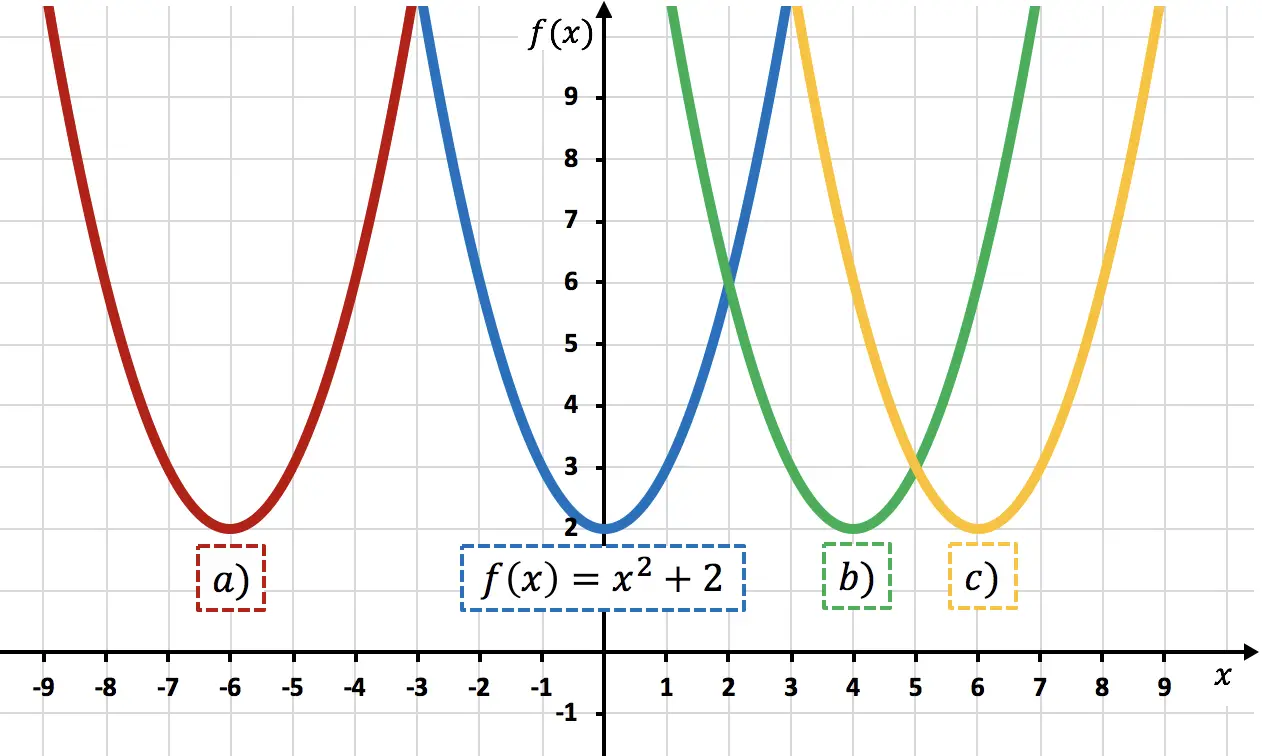
risolto problemi di trasformazione di funzioni

Vedi la soluzione

Funzione

$f(x)=(x-6)^2+2$

è la funzione

$f(x)=x^2+2$

spostato di 6 unità a destra. Possiamo verificarlo calcolando

$f(x-6):$

$f(x)=x^2+2$

$f(x-6)=(x-6)^2+2$

Pertanto, la rappresentazione di

$f(x)=(x-6)^2+2$

corrisponde alla parabola c) , perché è spostata di 6 unità a destra rispetto a

$f(x)=x^2+2$

Questo può essere visto guardando i vertici delle parabole: la distanza tra i vertici della parabola

$f(x)=x^2+2$

ed il vertice della parabola c) è di 6 unità, quindi quest’ultima è spostata di 6 unità a destra rispetto alla prima.

Trasformazioni di funzioni: traslazioni, simmetria, espansione e compressione

Cosa sono le trasformazioni di funzioni?

Traslazioni o spostamenti di funzioni

Traslazione o movimento verticale di una funzione

Traslazione o spostamento orizzontale delle funzioni

Esempio di traslazione o spostamento di una funzione

Riflessione o simmetria di una funzione rispetto agli assi coordinati

Esempio di mirroring di una funzione

Espansioni e contrazioni di funzioni

Espansione e contrazione verticale di una funzione

Esempio di come espandere o comprimere una funzione

Esercizi risolti sulle trasformazioni di funzioni

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Esercizio 6

Esercizio 7

Lascia un commento Annulla risposta