Distanza tra un punto e una linea

Qui troverai la formula utilizzata per calcolare la distanza tra un punto e una linea. Inoltre, potrai vedere diversi esempi ed esercizi risolti sulle distanze tra punti e linee e, anche, le applicazioni che ha questa operazione (ad esempio, trovare la distanza tra linee parallele).

Formula per la distanza tra un punto e una linea

La distanza tra un punto e una linea è la distanza più breve tra quel punto e la linea. Matematicamente questa distanza minima equivale alla lunghezza del segmento tracciato dal punto alla linea e che è perpendicolare alla linea.

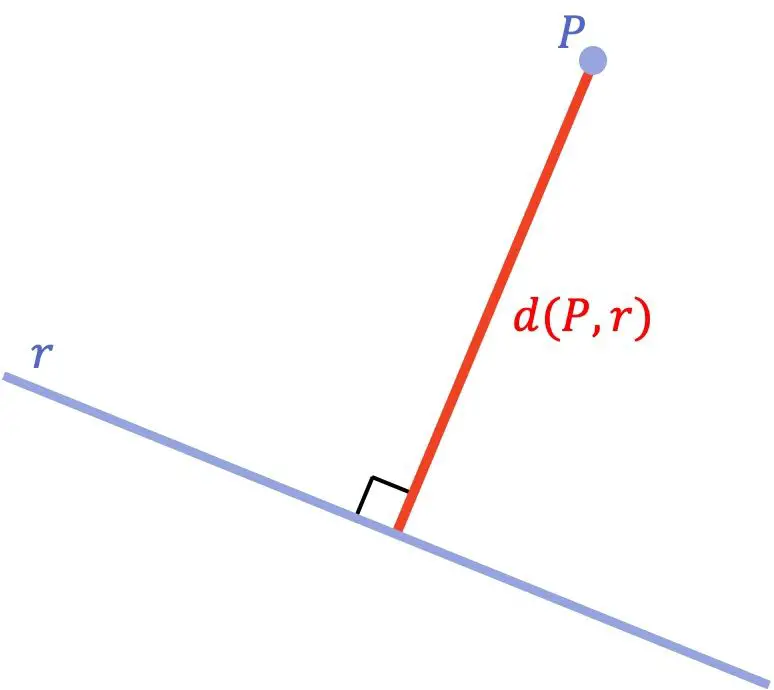
qual è la distanza tra un punto e una linea

Una volta visto il concetto geometrico di distanza tra un punto e una linea, vediamo qual è la formula utilizzata per calcolare tale distanza:

Data l’equazione implicita (o generale) di una linea e le coordinate di qualsiasi punto su un piano:

$r: \ Ax+By+C=0 \qquad \qquad P(p_x,p_y)$

La formula per la distanza tra un punto e una linea è:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Importante: notare che l’equazione della retta nella formula è sotto forma di equazione implicita (o generale), quindi se abbiamo la retta espressa in un altro tipo di equazione, dobbiamo passarla prima alla sua equazione implicita e poi possiamo applicare la formula.

Esempio di calcolo della distanza tra un punto e una linea

Di seguito puoi vedere un esempio di calcolo della distanza tra un punto e una linea:

Trova la distanza tra il punto
$P$

e la legge

$r:$

$P(2,-1) \qquad \qquad r: \ 3x+4y-5=0$

Per calcolare la distanza tra il punto e la linea, applica semplicemente la sua formula:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Ora sostituiamo ogni termine con il suo valore:

$d(P,r)= \cfrac{\lvert 3\cdot 2 + 4\cdot (-1)-5\rvert}{\sqrt{3^2+4^2}}$

E infine calcoliamo la distanza:

$d(P,r)= \cfrac{\lvert 6 -4-5\rvert}{\sqrt{9+16}} =\cfrac{\lvert -3 \rvert}{\sqrt{25}} = \mathbf{\cfrac{3}{5}}$

Distanza tra due rette parallele

Una delle applicazioni del calcolo della distanza tra una linea e un punto è trovare la distanza tra linee parallele.

Ovviamente, per comprendere il concetto che spiegheremo di seguito, devi sapere cosa sono le rette parallele , quindi se non conosci esattamente la loro definizione, ti lasciamo un link dove lo spieghiamo in dettaglio e potrai anche vedere degli esempi di rette parallele.

Per trovare la distanza tra due linee parallele, basta prendere un punto su una delle due linee e calcolare la distanza da quel punto all’altra linea.

Quindi, per determinare la distanza tra due linee parallele, viene utilizzata anche la formula per la distanza tra una linea e un punto.

D’altra parte, se utilizzando la formula otteniamo una distanza di 0 unità, ciò significa che le linee si toccano in un punto e, quindi, le linee non sono parallele, ma si intersecano, coincidenti o perpendicolari. Se vuoi, puoi verificare le differenze tra questo tipo di linee sul nostro sito.

Vediamo quindi come risolvere un problema di distanza tra due rette parallele attraverso un esempio:

Trova la distanza tra le seguenti due rette parallele:

$r: \ 2x-4y-6=0 \qquad \qquad s: \ -x+2y+4=0$

La prima cosa che dobbiamo fare è ottenere un punto su una delle linee (quella che desideri). In questo caso, calcoleremo un punto sulla linea

$s.$

Per fare ciò, devi dare un valore a una delle variabili, ad esempio faremo

$x=0:$

$-x+2y+4 =0 \ \xrightarrow{x \ = \ 0} \ -0+2y+4=0$

E ora cancelliamo l’altra variabile (

$y$

) dell’equazione ottenuta per sapere quanto vale a questo punto:

$2y=-4$

$y= \cfrac{-4}{2}$

$y= -2$

Pertanto il punto ottenuto dalla retta

$s$

Est:

$P(0,-2)$

E una volta che abbiamo già un punto su una linea, calcoliamo la distanza da quel punto all’altra linea usando la formula:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 2\cdot 0 + (-4)\cdot (-2) +(-6)\rvert}{\sqrt{2^2+(-4)^2}}= \cfrac{2}{\sqrt{20}}=\bm{0,45}$

Risolti problemi di distanza tra un punto e una linea

Esercizio 1

Calcola la distanza tra i punti

$P$

e la legge

$r:$

$P(4,2) \qquad \qquad r: \ 5x-3y+6=0$

vedi soluzione

Per trovare la distanza tra un punto e una linea, applica semplicemente la sua formula:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Sostituiamo ogni termine con il suo valore e calcoliamo la distanza:

$d(P,r)= \cfrac{\lvert 5\cdot 4 + (-3)\cdot 2+6\rvert}{\sqrt{5^2+(-3)^2}}=\cfrac{20}{\sqrt{34}}= \bm{3,43}$

Esercizio 2

Qual è la distanza tra il punto

$P$

e la legge

$r$

$P(-3,-1) \qquad \qquad r: \ y=-3x+5$

vedi soluzione

In questo caso l’equazione della retta è in forma implicita (o generale). Invece, per utilizzare la formula per la distanza da un punto a una linea, la linea deve essere espressa come un’equazione implicita. Dobbiamo quindi prima trasformare la retta e passarla ad un’equazione implicita (basta passare tutti i termini dallo stesso lato dell’equazione):

$r: \ 3x+y-5=0$

E una volta che la linea è già in forma esplicita, possiamo ora usare la formula per la distanza tra un punto e una linea:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Sostituiamo quindi ad ogni termine il suo valore e calcoliamo la distanza:

$d(P,r)= \cfrac{\lvert 3\cdot (-3) + 1\cdot (-1)-5\rvert}{\sqrt{3^2+1^2}}=\cfrac{\lvert -9-1-5\rvert}{\sqrt{9+1}}=\cfrac{15}{\sqrt{10}}= \bm{4,74}$

Esercizio 3

Qual è la distanza tra le due linee seguenti?

$r: \ x+3y-4=0 \qquad \qquad s: \ 2x+6y+6=0$

vedi soluzione

Per prima cosa verificheremo che si tratti di due rette parallele. Per questo, i coefficienti delle variabili

$x$

$y$

devono essere proporzionali tra loro ma non ai termini indipendenti:

$\cfrac{1}{2} = \cfrac{3}{6}\neq \cfrac{-4}{6} \ \longrightarrow \ \text{Paralelas}$

In effetti le rette sono parallele, possiamo quindi applicare il procedimento.

Ora dobbiamo ottenere un punto da una delle linee (quella che desideri). In questo caso, calcoleremo un punto sulla linea

$s.$

Per fare ciò, è necessario assegnare un valore a una delle variabili, ad esempio faremo

$x=0:$

$2x+6y+6=0 \ \xrightarrow{x \ = \ 0} \ 2\cdot 0+6y+6=0$

E ora cancelliamo l’altra variabile (

$y$

) dell’equazione ottenuta per conoscerne il valore a questo punto:

$6y=-6$

$y= \cfrac{-6}{6}$

$y= -1$

In modo che il punto ottenuto dalla linea

$s$

Est:

$P(0,-1)$

Una volta conosciuto un punto su una linea, calcoliamo la distanza da quel punto all’altra linea con la formula:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 1\cdot 0 + 3\cdot (-1) +(-4)\rvert}{\sqrt{1^2+3^2}}= \cfrac{7}{\sqrt{10}}=\bm{2,21}$

Esercizio 4

Calcolare il valore dell’incognita

$k$

in modo che la distanza tra il punto

$P$

e la legge

$r$

cioè 5 unità.

$P(-2,5) \qquad \qquad r: \ 12x-5y+k=0$

vedi soluzione

Dobbiamo prima applicare la formula per la distanza tra un punto e una linea:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Ora sostituiamo ogni termine con il suo valore e semplifichiamo l’espressione:

$d(P,r)= \cfrac{\lvert 12\cdot (-2) + (-5)\cdot 5+k\rvert}{\sqrt{12^2+(-5)^2}}= \cfrac{\lvert -24-25+k\rvert}{\sqrt{169}}=\cfrac{\lvert -49+k\rvert}{13}$

La formulazione del problema ci dice che la distanza tra il punto e la linea deve essere uguale a 5, quindi uguagliamo l’espressione precedente a 5:

$\cfrac{\lvert -49+k\rvert}{13}=5$

E risolviamo l’equazione risultante. Al numeratore della frazione c’è un valore assoluto, quindi dobbiamo analizzare separatamente quando il valore assoluto è positivo e quando è negativo:

$\cfrac{+(-49+k)}{13}=5$