Distanza tra due linee nello spazio (in R3)

In questa pagina troverai come si calcola la distanza tra due linee nello spazio (in R3), qualunque sia la loro tipologia (linee parallele, secanti, coincidenti, secanti, perpendicolari, ecc.). Inoltre, potrai vedere esempi ed esercizi risolti passo dopo passo.

Come calcolare la distanza tra due linee

La distanza tra due linee è la distanza minima tra qualsiasi punto su una linea e qualsiasi punto sull’altra linea. Questa distanza corrisponde alla lunghezza del segmento che va da una linea all’altra e che, allo stesso tempo, è perpendicolare ad entrambe le linee.

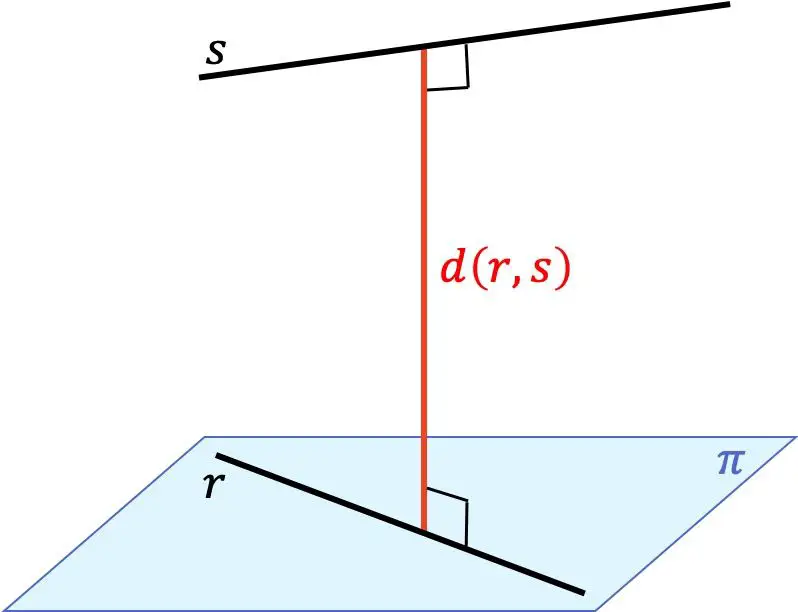
distanza tra due linee nello spazio (in R3)

Quindi, trovare la distanza tra due linee diverse nello spazio tridimensionale (3D) dipende dalla posizione relativa tra loro:

Se le due linee coincidono o si intersecano , la distanza tra le due linee è zero, perché si intersecano (almeno) in un punto.
Quando le due linee sono parallele , dobbiamo prendere un punto qualsiasi su una delle linee e calcolare la distanza tra quel punto e l’altra linea (sotto hai un esempio di come farlo).
Se le due linee si intersecano nello spazio, dobbiamo applicare la formula per la distanza tra due linee che si intersecano (vedi sotto per una spiegazione dettagliata).

Quindi, per calcolare la distanza tra due linee, bisogna prima sapere di che tipo di linee sono e poi, a seconda dei casi, utilizzare una formula o un’altra. Pertanto è importante che tu sappia già come trovare la posizione relativa di due linee nello spazio prima di continuare, ma se non ricordi come è stato fatto nel link vedrai una spiegazione molto completa oltre ad esempi ed esercizi risolti passo dopo passo.

Come trovare la distanza tra due linee parallele nello spazio

Il calcolo della distanza tra due linee parallele nello spazio (in R3) si fa allo stesso modo che nel piano (in R2): devi prendere un punto su una qualsiasi delle due linee e trovare la distanza di questo punto sull’altra linea.

Pertanto, la formula per calcolare la distanza da un punto a una linea in 3 dimensioni (e che viene utilizzata per determinare la distanza tra due linee parallele) è:

$d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}$

Oro:

$\lvert \vv{\text{v}}_r \rvert$

è il modulo del vettore direzione della linea

$r.$
$Q$

è un punto sulla linea

$r,$

$P$

un punto sulla linea

$s$

E

$\vv{QP}$

il vettore definito dai due punti
$\lvert \vv{QP} \times \vv{\text{v}}_r \rvert$

è l’entità del prodotto vettoriale tra i vettori

$\vv{QP}$

E

$\vv{\text{v}}_r$

Ad esempio, risolveremo un problema di distanza tra 2 linee parallele nello spazio:

Qual è la distanza tra le seguenti due rette parallele?

$r: \ (x,y,z) = (2,1,1) + t(-1,3,2)$

$s: \ (x,y,z) = (-2,4,1) + t(2,-6,-4)$

Entrambe le linee sono espresse sotto forma di un’equazione vettoriale, quindi possiamo facilmente trovare il vettore direzione e un punto di ciascuna di esse:

$\displaystyle r : \ \begin{cases}\vv{\text{v}}_r=(-1,3,2) \\[1.7ex] Q(2,1,1) \end{cases} \qquad \qquad s: \ \begin{cases}\vv{\text{v}}_s=(2,-6,-4) \\[1.7ex] P(-2,4,1) \end{cases}$

Se hai dei dubbi su come determinare il vettore direzione e un punto di una retta, ti consigliamo di dare un’occhiata alla spiegazione dell’equazione della retta . Lì lo abbiamo spiegato per tutte le equazioni della retta, perché trovare il vettore direzione e un punto che appartiene ad una retta dipende dal tipo di equazione in cui è espressa la retta.

Ora, per trovare la distanza tra due rette parallele, dobbiamo applicare la formula per la distanza da un punto a una retta:

$d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}$

Quindi da un lato calcoliamo il modulo del vettore risultante dal prodotto vettoriale. Se hai dubbi su come viene calcolato, puoi consultare la formula del prodotto vettoriale , dove, inoltre, potrai vedere esempi ed esercizi risolti di questa operazione tra vettori.

$\vv{QP} = Q - P = (2,1,1)-(-2,4,1) = (4,-3,0)$

$\vv{QP} \times \vv{\text{v}}_r =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 4&-3&0 \\[1.1ex] -1&3&2 \end{vmatrix}=-6\vv{i} -8\vv{j}+9\vv{k}$

$\left|\vv{QP} \times \vv{\text{v}}_r \right| =\sqrt{(-6)^2+(-8)^2+9^2} = \sqrt{36+64+81} = \sqrt{181}$

E, d’altra parte, troviamo la grandezza del vettore della linea

$r:$

$\lvert \vv{\text{v}}_r \rvert = \sqrt{(-1)^2+3^2+2^2} = \sqrt{1+9+4} = \sqrt{14}$

Infine, sostituiamo il valore di ciascun termine nella formula e calcoliamo la distanza tra le linee:

$d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}=\cfrac{\sqrt{181}}{\sqrt{14}} = \bm{3,60}$

Pertanto la distanza tra le due linee è pari a 3,60 unità.

Come determinare la distanza tra due linee che si intersecano nello spazio

Come abbiamo visto all’inizio, il metodo per determinare la distanza tra due linee che si intersecano è diverso dal procedimento per le distanze tra linee parallele.

distanza tra linee incrociate nello spazio

Pertanto, esistono diversi metodi per determinare la distanza tra due linee che si intersecano nello spazio. In questa pagina spiegheremo solo una procedura, la più semplice, perché gli altri due metodi sono più lunghi e complicati, infatti, praticamente non vengono utilizzati.

Sia il vettore direzione e qualsiasi punto di due linee che si intersecano:

$\displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}$

La formula per la distanza tra due linee che si intersecano è:

$d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}$

Oro

$\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|$

è il valore assoluto del prodotto misto dei vettori

$\vv{\text{u}}, \vv{\text{v}}$

e il vettore definito dai punti

$A$

$B$

. E d’altra parte,

$\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert$

è l’ampiezza del prodotto vettoriale tra i vettori di direzione delle due linee incrociate.

Affinché tu possa vedere come determinare la distanza tra due linee incrociate, risolveremo un problema come esempio:

Qual è la distanza tra le prossime due linee che si intersecano?

$r: \ \cfrac{x-1}{2} = \cfrac{y-2}{4} = \cfrac{z+2}{-1}$

$s: \ \cfrac{x-3}{1} = \cfrac{y+1}{3} = \cfrac{z-1}{-2}$

Per prima cosa dobbiamo identificare il vettore direzione e un punto su ciascuna linea. Le due rette sono espresse sotto forma di equazione continua, quindi:

$\displaystyle r: \ \begin{cases} \vv{\text{u}} =(2,4,-1) \\[2ex] A(1,2,-2) \end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}}=(1,3,-2) \\[2ex] B(3,-1,1)\end{cases}$

E ora applichiamo la formula per la distanza tra due linee che si intersecano:

$d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}$

Da un lato risolviamo il prodotto misto (o triplo prodotto scalare):

$\vv{AB} = B - A = (3,-1,1) - (1,2,-2) = (2,-3,3)$

$\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right| =\left| \begin{vmatrix} 2&4&-1 \\[1.1ex] 1&3&-2 \\[1.1ex] 2&-3&3 \end{vmatrix}\right| = \left| -13 \right| =13$

E, d’altra parte, troviamo il modulo del prodotto incrociato (o prodotto incrociato):

$\vv{\text{u}} \times \vv{\text{v}} =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 2&4&-1 \\[1.1ex] 1&3&-2 \end{vmatrix}=-5\vv{i} +3\vv{j}+2\vv{k}$

$\left| \vv{\text{u}} \times \vv{\text{v}} \right| =\sqrt{5^2+3^2+2^2} = \sqrt{25+9+4} = \sqrt{38}$

Infine, sostituiamo il valore di ciascun termine nella formula per la distanza tra due linee incrociate:

$d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} = \cfrac{13}{\sqrt{38}}= \bm{2,11}$

Distanza tra due linee nello spazio (in r3)

Come calcolare la distanza tra due linee

Come trovare la distanza tra due linee parallele nello spazio

Come determinare la distanza tra due linee che si intersecano nello spazio

Lascia un commento Annulla risposta