Distanza da una linea a un piano nello spazio

Qui troverai come si calcola la distanza da una linea a un piano e, inoltre, potrai vedere esempi ed esercizi risolti passo dopo passo.

Qual è la distanza tra una linea e un piano?

Nella geometria analitica, la distanza tra una linea e un piano nello spazio dipende dalla posizione relativa tra questi due elementi geometrici:

Se la linea è compresa nel piano oppure se la linea e il piano sono paralleli , la distanza che li separa è zero.
Se la linea è parallela al piano , la distanza dalla linea al piano si trova prendendo un punto qualsiasi della linea e calcolando la distanza da quel punto al piano.

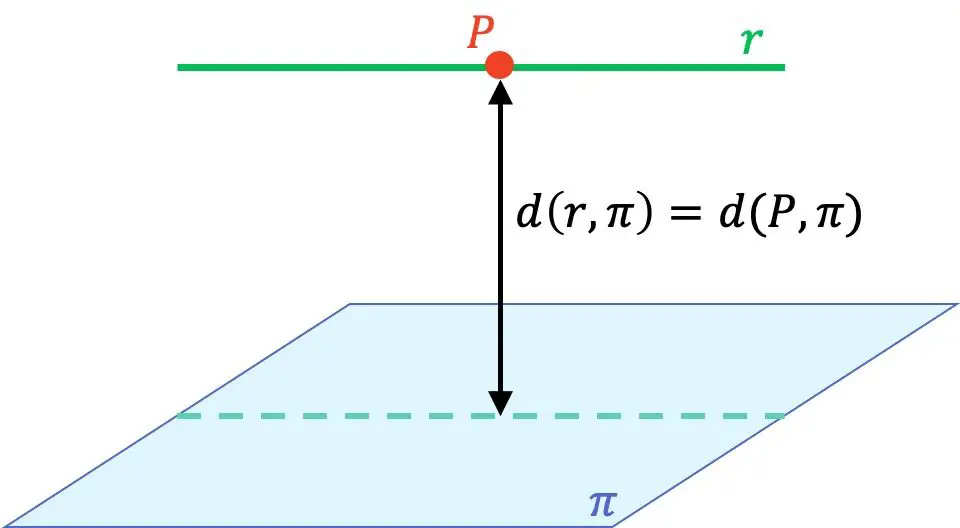
distanza da una linea ad un piano nello spazio

Pertanto, per calcolare la distanza da una linea a un piano, è essenziale sapere come determinare la posizione relativa tra una linea e un piano e come calcolare la distanza tra un punto e un piano . Quindi se non vi sono del tutto chiare o non conoscete le formule, vi consigliamo di dare prima un’occhiata alle pagine collegate, dove troverete spiegazioni, esempi ed esercizi risolti passo dopo passo.

Esempio di calcolo della distanza tra una linea e un piano

Affinché tu possa vedere come trovare la distanza tra una linea e un piano nello spazio (in R3), risolveremo un problema come esempio:

Quanto è lontana la linea?
$r$

sull’aereo

$\pi$

?

$\displaystyle r: \ \begin{cases}x=-2+t \\[1.7ex] y=1-3t \\[1.7ex] z=-1+2t\end{cases}$

$\pi : \ 4x+2y+z-6=0$

Per trovare la distanza tra la linea e il piano, devi prima conoscere la posizione relativa tra i due.

Da un lato, la linea è definita sotto forma di equazioni parametriche, quindi il suo vettore direzione e il punto attraverso il quale passa sono:

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(1,-3,2) \\[2ex] P(-2,1,-1) \end{cases}$

E, d’altra parte, il vettore normale al piano è:

$\vv{n} =(4,2,1)$

Pertanto, per determinare la posizione relativa tra il piano e la linea, è necessario calcolare il prodotto scalare tra il vettore direzione della linea e il vettore normale al piano:

$\begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (1,-3,2) \cdot (4,2,1) \\[2ex] & = 1 \cdot 4-3 \cdot 2 +2\cdot 1 \\[2ex] &= 4 -6 +2 \\[2ex] & = 0\end{aligned}$

Il risultato del prodotto scalare è zero, quindi la linea può essere contenuta solo nel piano o essere parallela ad esso. Quindi, per scoprire di quale caso si tratta, sostituiamo le coordinate cartesiane del punto sulla retta nell’equazione del piano:

$4x+2y+z-6=0 \ \xrightarrow{P(-2,1,-1)} \ 4\cdot (-2) +2\cdot 1 -1-6= 0$

$-8+2-1-6 = 0$

$-13 \neq 0$

Sostituendo il punto della retta nell’equazione del piano otteniamo una disuguaglianza, quindi il punto non rispetta l’equazione del piano e, di conseguenza, la retta e il piano sono paralleli.

Una volta che sappiamo che la linea e il piano sono paralleli, possiamo calcolare la distanza geometrica tra loro. Per fare ciò, prendiamo il punto sulla linea e calcoliamo la distanza da quel punto all’aereo.

$P(-2,1,-1) \qquad \qquad \pi: \ 4x+2y+z-6=0$

Quindi usiamo la formula per la distanza da un punto a un piano:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Ora sostituiamo il valore di ciascuna incognita nella formula:

$d(P,\pi) = \cfrac{\lvert 4\cdot (-2)+2\cdot 1+1\cdot (-1)-6\rvert}{\sqrt{4^2+2^2+1^2}}$

E, infine, eseguiamo le operazioni:

$d(P,\pi) = \cfrac{\lvert -8+2-1-6\rvert}{\sqrt{16+4+1}}$

$d(P,\pi) = \cfrac{\lvert -13\rvert}{\sqrt{21}}$

$d(P,\pi) = \cfrac{13}{\sqrt{21}}$

In modo che la distanza tra la linea e il piano sia equivalente alla distanza tra il punto e il piano calcolata:

$\bm{d(r,\pi)=d(P,\pi) = }\cfrac{\bm{13}}{\bm{\sqrt{21}}}$

Ovviamente la distanza deve darci sempre un valore positivo, perché le distanze sono sempre positive. Se otteniamo un risultato negativo significa che abbiamo commesso un errore nel fare un passo.

Qual è la distanza tra una linea e un piano?

Esempio di calcolo della distanza tra una linea e un piano

Lascia un commento Annulla risposta