In questa sezione vedremo come discutere e risolvere un sistema di equazioni con il metodo di Gauss-Jordan . Cioè, determinare se si tratta di un sistema compatibile determinato (DCS), un sistema compatibile indeterminato (ICS) o un sistema incompatibile. Inoltre, troverai esempi ed esercizi risolti per poter praticare e assimilare perfettamente i concetti.
Per capire cosa spiegheremo dopo, è importante che tu sappia già come risolvere un sistema utilizzando il metodo di Gauss , quindi ti consigliamo di dare un’occhiata prima di continuare.
Sistemi compatibili determinati con il metodo di Gauss
Finché lo è l’ultima riga della matrice gaussiana
![]()
, Essere
![]()
E
![]()
due numeri qualsiasi, questo è un SCD (System compatibile determinato). Pertanto, il sistema ha una soluzione unica .
La stragrande maggioranza dei sistemi sono SCD.
Esempio:
Ad esempio, abbiamo questo sistema:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bab5d5823e45833aa691a3510a2a23eb_l3.png)
La cui matrice espansa è:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}} \ \longrightarrow \ \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f8daea11edeedfd6b86bb251fe19032_l3.png)
Per risolvere il sistema dobbiamo operare sulle righe della matrice e convertire a 0 tutti gli elementi sotto la diagonale principale. Quindi dalla seconda riga sottraiamo la prima riga e dalla terza riga sottraiamo la prima riga moltiplicata per 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3 -2f_1} & \end{array} \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-d68ac25745ddc71d1e7f55f68dd4ea7a_l3.png)
Una volta che tutti i numeri sotto la diagonale principale sono 0, torniamo a trasformare il sistema in forma di equazione:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 6y+2z=0\\[2ex] 1z=-3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4457f1b034e72c6945bfe609eff52b9a_l3.png)
Quindi questo sistema è SCD , poiché la matrice è spostata e l’ultima riga è del tipo
![]()
. Pertanto lo risolviamo come sempre: eliminando le incognite dalle equazioni dal basso verso l’alto.
![]()
![]()
![]()
Ora che conosciamo z, inseriamo il suo valore nella seconda equazione per trovare il valore di
![]()
:
![]()
![]()
![]()
![]()
![]()
E infine facciamo lo stesso con la prima equazione: sostituiamo i valori delle altre incognite e risolviamo
![]()
:
![]()
![]()
![]()
![]()
![]()
![]()
La soluzione del sistema di equazioni è quindi:
![]()
Sistemi incompatibili secondo il metodo di Gauss
Quando nella matrice di Gauss abbiamo una riga con tre 0 di seguito e un numero
![]()
, è un IS (Sistema Incompatibile) e, pertanto, il sistema non ha soluzione .
Esempio:
Ad esempio, immagina che dopo aver operato con la matrice gaussiana di un sistema, ci ritroviamo:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & 1 & -1 & 0 \\[2ex] 0 & 3 & 1 & -1 \\[2ex] 0 & 0 & 0 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-defe65fa616eff800314ebc6dc6f552b_l3.png)
Come l’ultima riga
![]()
, cioè tre 0 seguiti da un numero finale, è un IF (Sistema Incompatibile) e quindi il sistema non ha soluzione .
Sebbene non sia necessario saperlo, di seguito vedrai perché non ha una soluzione.
Se prendiamo l’ultima riga, avremmo questa equazione:
![]()
Questa equazione non sarà mai soddisfatta, perché qualunque valore assuma z , moltiplicandolo per 0 non darà mai 2 (qualsiasi numero moltiplicato per 0 dà sempre 0). E poiché questa equazione non sarà mai soddisfatta, il sistema non ha soluzione.
Sistemi compatibili indeterminati dal metodo gaussiano
Ogni volta che una riga della matrice gaussiana è riempita con 0
![]()
, è un SCI (Sistema Compatibile Indeterminato), e, quindi, il sistema ha infinite soluzioni .
Vediamo un esempio di come risolvere un ICS:
Esempio:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-18a63dfebc1f23923714e475aad2e808_l3.png)
Come sempre, realizziamo prima la matrice espansa del sistema :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\} \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f273040101827fdfea5c9a4858be5567_l3.png)
Ora vogliamo che tutti i numeri sotto la diagonale principale siano 0. Quindi, alla seconda riga aggiungiamo la prima riga moltiplicata per -2:
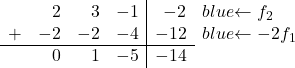
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c889a6f147c6b0430731aa778121af52_l3.png)
Per convertire 3 in 0, nella terza riga aggiungiamo la prima riga moltiplicata per -3:
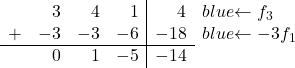
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -3f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c5acccc51108267fef6d3320068743aa_l3.png)
Per convertire l’1 nell’ultima riga in 0, nella terza riga aggiungiamo la seconda riga moltiplicata per -1:

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a02e4819adfbe7b80d2952f87f113757_l3.png)
Poiché l’ultima riga è tutta 0 , possiamo rimuoverla:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6aea469dceab08e6aa62571922eb2824_l3.png)
E poiché abbiamo un’intera riga piena di 0, questo è uno SCI.
Ci ritroviamo quindi con il seguente sistema:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y+2z=6 \\[2ex] y-5z=-14 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-598c031f4cba5a865952a57ed46f0f95_l3.png)
Quando il sistema è uno SCI è necessario prendere il valore del parametro da un’incognita
![]()
. E dobbiamo risolvere il sistema in base a questo parametro
![]()
.
Pertanto assegniamo il valore di
![]()
alla z :
![]()
Anche se avremmo potuto scegliere anche qualsiasi altra incognita di cui apprezzare il valore
![]()
.
Ora isoliamo y dalla seconda equazione e lasciamo che sia una funzione di
![]()
:
![]()
![]()
![]()
E infine eliminiamo x dalla prima equazione e la lasciamo anche in funzione di
![]()
:
![]()
![]()
![]()
![]()
Le soluzioni del sistema sono quindi:
![]()
Come puoi vedere, quando il sistema è SCI lasciamo le soluzioni a seconda del parametro
![]()
. E ricorda che ha infinite soluzioni, perché a seconda del valore che assume
![]()
, la soluzione sarà l’una o l’altra.
Prima di passare agli esercizi risolti, devi sapere che sebbene in questo articolo utilizziamo il metodo di Gauss, un altro modo per discutere e risolvere sistemi di equazioni lineari è il teorema di Rouche . In effetti, probabilmente è più usato.
Esercizi risolti per la discussione di sistemi di equazioni utilizzando il metodo Gauss-Jordan
Esercizio 1
Determina quale tipo di sistema è coinvolto e risolvi il seguente sistema di equazioni utilizzando il metodo di Gauss:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-be4ba1bd1ce7452e66c5189d995d948c_l3.png)
La prima cosa che dobbiamo fare è la matrice estesa del sistema:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex] 3 & 3 & 6 & 9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b600f3fc0d79a06eb972dbacb673a780_l3.png)
Ora dobbiamo rendere 0 tutti i numeri sotto l’array principale.
Eseguiamo quindi operazioni sulle righe per cancellare gli ultimi due termini della prima colonna:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex]3 & 3 & 6 & 9 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 2f_1} \\[2ex] \xrightarrow{f_3 - 3f_1}& \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & 1 & -4 \\[2ex] 0 & 0 & 0 & -9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a1d832d5bb115666614ae96822c360eb_l3.png)
Abbiamo ottenuto una riga della matrice composta da tre 0 seguiti da un numero. Si tratta quindi di un IS (Sistema Incompatibile) e il sistema non ha soluzione.
Esercizio 2
Determina di che tipo di sistema si tratta e trova la soluzione del seguente sistema di equazioni utilizzando il metodo di Gauss:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7f5aba495f2c6a301e923ee3c6238012_l3.png)
La prima cosa che dobbiamo fare è la matrice estesa del sistema:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f8bb5e5ab85946bddad72067fe17d937_l3.png)
Ora dobbiamo rendere 0 tutti i numeri sotto l’array principale.
Eseguiamo quindi operazioni sulle righe per cancellare gli ultimi due termini della prima colonna:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 2f_1} \\[2ex] \xrightarrow{f_3 + f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-83e48becaaa6683719ac57eb7d118943_l3.png)
Ora proviamo a rimuovere l’ultimo elemento dalla seconda colonna:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-16a1afc0eb224ee5f05c9e313586854d_l3.png)
Ma otteniamo un’intera riga di 0. Quindi questo è uno SCI e il sistema ha infinite soluzioni.
Ma poiché si tratta di un ICS, possiamo risolvere il sistema in base a
![]()
. Eliminiamo quindi la riga 0:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-5c838c5f1b229d4c8a43ac9ddd8e3629_l3.png)
Esprimiamo ora la matrice sotto forma di un sistema di equazioni in incognite:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-2y+3z=1 \\[2ex] 1y+5z=7 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b3fd941d33fec646d16b8181430c9986_l3.png)
Diamo il valore di
![]()
Per
![]()
![]()
Sostituiamo il valore di
![]()
nella seconda equazione per trovare il valore di
![]()
![]()
![]()
![]()
E facciamo lo stesso con la prima equazione: sostituiamo i valori delle altre incognite e cancelliamo
![]()
![]()
![]()
![]()
![]()
La soluzione del sistema di equazioni è quindi:
![]()
Esercizio 3
Trova di che tipo di sistema si tratta e risolvi il seguente sistema di equazioni con il metodo di Gauss:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b04370b42854e53c650ca0eae14aadb5_l3.png)
La prima cosa che dobbiamo fare è la matrice estesa del sistema:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff2c7644e19fdf405f3c5c42ffc0ee98_l3.png)
Per applicare il metodo di Gauss, è più semplice se il primo numero nella prima riga è 1. Cambieremo quindi l’ordine delle righe 1 e 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 \rightarrow f_2} \\[2ex] \xrightarrow{f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-471d89605d4bf6ddef1896a8fbe4c5ea_l3.png)
Ora dobbiamo rendere 0 tutti i numeri sotto l’array principale.
Eseguiamo quindi operazioni sulle righe per cancellare gli ultimi due termini della prima colonna:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 4f_1} \\[2ex] \xrightarrow{f_3 -f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f4d5cbc50b87927077018175c4678e90_l3.png)
Ora convertiamo l’ultimo elemento della seconda colonna in zero:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{8f_3 + f_2} \end{array} \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-9013720883fd719e2bd0779bfbaa7a9f_l3.png)
Questo sistema è SCD , poiché siamo riusciti a spostare la matrice e l’ultima riga è del tipo
![]()
. Pertanto, avrà una soluzione unica.
Una volta che tutti i numeri sotto la diagonale principale sono 0, possiamo risolvere il sistema di equazioni. Per fare ciò, esprimiamo nuovamente la matrice sotto forma di un sistema di equazioni in incognite:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+1z=2 \\[2ex] -16y-3z=-12 \\[2ex] 5z=20 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0f0433738d5d0a22bdd3b04dbd44fd1e_l3.png)
E risolviamo le incognite delle equazioni dal basso verso l’alto. Risolviamo prima l’ultima equazione:
![]()
![]()
Ora sostituiamo il valore di z nella seconda equazione per trovare il valore di y:
![]()
![]()
![]()
![]()
![]()
E facciamo lo stesso con la prima equazione: sostituiamo i valori delle altre incognite e risolviamo per x:
![]()
![]()
![]()
![]()
La soluzione del sistema di equazioni è quindi:
![]()
Esercizio 4
Determina di che tipo di sistema si tratta e risolvi il seguente sistema di equazioni con il metodo di Gauss:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e8a133547b4719d7833a792550fd322_l3.png)
La prima cosa che dobbiamo fare è la matrice estesa del sistema:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-cc41f78456a922a0fbff419d336b0b46_l3.png)
Ora dobbiamo rendere 0 tutti i numeri sotto l’array principale.
Eseguiamo quindi operazioni sulle righe per cancellare gli ultimi due termini della prima colonna:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 3f_1} \\[2ex] \xrightarrow{f_3 + 2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff92912f653c6aca7ceb7c990c9635a3_l3.png)
Ora proviamo a rimuovere l’ultimo elemento dalla seconda colonna:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c6904a64a721f3a92bef8c6b7d713cf_l3.png)
Ma otteniamo un’intera riga di 0. Quindi questo è uno SCI e il sistema ha infinite soluzioni.
Ma poiché si tratta di un ICS, possiamo risolvere il sistema in base a
![]()
. Eliminiamo quindi la riga 0:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6d856e2c1246f3629d68a7bcd3cd759a_l3.png)
Esprimiamo ora la matrice sotto forma di un sistema di equazioni in incognite:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-1y+4z=2 \\[2ex] -6y+15z=13 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a4cf1265bfc12f94580de183230c8b7c_l3.png)
Diamo il valore di
![]()
Per
![]()
![]()
Sostituiamo il valore di
![]()
nella seconda equazione per trovare il valore di
![]()
![]()
![]()
![]()
![]()
E facciamo lo stesso con la prima equazione: sostituiamo i valori delle altre incognite e cancelliamo
![]()
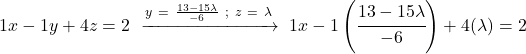
![]()
![]()
Abbiamo una somma con frazioni. Pertanto, riduciamo tutti i termini a un denominatore comune:
![]()
![]()
Dato che ora hanno tutti lo stesso denominatore, possiamo raggrupparli in un’unica frazione:
![]()
Ed infine operiamo sul numeratore:
![]()
![]()
La soluzione del sistema di equazioni è quindi:
![]()