Discussione dei sistemi di equazioni con parametri -

In questa pagina vedremo come discutere e risolvere un sistema di equazioni con parametri . Inoltre, troverai esempi ed esercizi risolti di sistemi di equazioni lineari con cui esercitarti.

D’altra parte, per analizzare sistemi di equazioni lineari è importante che tu sappia qual è la regola di Cramer e qual è il teorema di Rouché–Frobenius , perché li useremo costantemente.

Esempio di sistema di equazioni lineari con parametri

Discuti e risolvi il seguente sistema di equazioni in termini del parametro m :

$\begin{cases} x+y+2z= 2 \\[1.5ex] -x+my+2z=0 \\[1.5ex] 3x+mz = 4\end{cases}$

Per prima cosa realizziamo la matrice A e la matrice estesa A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & m & 2 & 0 \\[1.1ex] 3 & 0 & m & 4 \end{array} \right)$

Ora risolviamo il determinante di A utilizzando la regola di Sarrus, per vedere di che rango è la matrice:

$\displaystyle\begin{aligned} \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} & =m^2+6+0-6m-0+m \\ & = m^2-5m+6 \end{aligned}$

Quindi il risultato del determinante di A dipende dal valore di m . Vedremo quindi per quali valori di m il determinante svanisce. Per fare ciò impostiamo il risultato uguale a 0 :

$\displaystyle m^2-5m+6 = 0$

E risolviamo l’equazione quadratica con la formula:

$\displaystyle m = \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle m = \cfrac{-(-5) \pm \sqrt{(-5)^2-4\cdot 1 \cdot 6}}{2 \cdot 1} = \cfrac{5 \pm \sqrt{25-24}}{2} =\cfrac{5 \pm 1}{2} = \begin{cases} \bm{m = 3} \\[2ex] \bm{m =2} \end{cases}$

Quindi quando m è uguale a 2 o 3, il determinante di A sarà 0. E quando m è diverso da 2 e diverso da 3, il determinante di A sarà diverso da 0.

Dobbiamo quindi analizzare ogni caso separatamente:

m≠3 e m≠2:

Come abbiamo appena visto, quando il parametro m è diverso da 2 e 3, il determinante della matrice A è diverso da 0. Pertanto il rango di A è 3 .

$\displaystyle rg(A)=3$

Inoltre, anche il rango della matrice A’ è 3 , perché al suo interno c’è una sottomatrice 3×3 il cui determinante è diverso da 0. E non può essere di rango 4 poiché ‘non possiamo fare un determinante 4×4.

$\displaystyle rg(A')=3$

Allora, poiché il rango della matrice A è pari al rango della matrice A’ e al numero di incognite del sistema (3), per il teorema di Rouché-Frobenius sappiamo che si tratta di un Sistema Determinato Compatibile (SCD) :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

Una volta che sappiamo che il sistema è un sistema determinato compatibile (DCS), applichiamo la regola di Cramer per risolverlo. Per fare ciò ricordiamo che la matrice A, il suo determinante e la matrice A’ sono:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} = m^2-5m+6$

Per calcolare x con la regola di Cramer, cambiamo la prima colonna del determinante della matrice A nella colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle\bm{x} = \cfrac{\begin{vmatrix} 2 & 1 & 2\\[1.1ex]0&m&2 \\[1.1ex] 4 & 0 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{2m^2+8-8m}{m^2-5m+6}$

Per calcolare y con la regola di Cramer, cambiamo la seconda colonna del determinante di A nella colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 0 & 2 \\[1.1ex] 3 & 4 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-4+2m}{m^2-5m+6}$

Per calcolare z con la regola di Cramer, cambiamo la terza colonna del determinante di A nella colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-2m+4}{m^2-5m+6}$

Pertanto, la soluzione del sistema di equazioni per il caso m≠3 e m≠2 è:

$\displaystyle \bm{x =} \cfrac{\bm{2m^2+8-8m}}{\bm{m^2-5m+6}} \qquad \bm{y=} \cfrac{\bm{-4+2m}}{\bm{m^2-5m+6}} \qquad \bm{z =} \cfrac{\bm{-2m+4}}{\bm{m^2-5m+6}}$

Come puoi vedere, in questo caso la soluzione del sistema di equazioni è una funzione di m.

Una volta trovata la soluzione per quando m è diverso da 2 e 3, risolveremo il sistema per quando m è uguale a 2:

m=2:

Analizzeremo ora il sistema quando il parametro m è uguale a 2. In questo caso le matrici A e A’ sono:

$\displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 2 & 2 \\[1.1ex] 3 & 0 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 2 & 2 & 0 \\[1.1ex] 3 & 0 & 2 & 4 \end{array} \right)$

Come abbiamo visto in precedenza, quando m=2 il determinante di A è 0. Pertanto la matrice A non è di rango 3. Ma al suo interno ha 2×2 determinanti diversi da 0, ad esempio:

$\displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0$

Quindi, in questo caso , il rango di A è 2 :

$\displaystyle rg(A)=2$

Una volta noto il rango della matrice A, calcoliamo il rango di A’. Il determinante delle prime 3 colonne dà 0, quindi proviamo gli altri possibili determinanti 3×3 nella matrice A’:

$\displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 0 & 2 & 4 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 2 & 4 \end{vmatrix}=0\qquad \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}=0$

Tutti i possibili determinanti della dimensione 3×3 danno 0. Ma, ovviamente, la matrice A’ ha lo stesso determinante 2×2 non 0 della matrice A:

$\displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0$

Pertanto anche la matrice A’ è di rango 2 :

$\displaystyle rg(A')=2$

Quindi, poiché il rango della matrice A è uguale al rango della matrice A’ ma questi due sono inferiori al numero di incognite del sistema (3), sappiamo dal teorema di Rouché-Frobenius che è Questo è un sistema indeterminatamente compatibile (ICS):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

Poiché si tratta di un ICS, dobbiamo trasformare il sistema per risolverlo. Per fare ciò dobbiamo prima eliminare un’equazione dal sistema, in questo caso elimineremo l’ultima equazione:

$\begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \\[1.5ex] \cancel{3x+2z = 4} \end{cases} \longrightarrow \quad \begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0\end{cases}$

Ora convertiamo la variabile z in λ:

$\begin{cases}x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+y+2\lambda= 2 \\[1.5ex] -x+2y+2\lambda=0\end{cases}$

E mettiamo i termini con λ con i termini indipendenti:

$\begin{cases}x+y=2-2\lambda \\[1.5ex] -x+2y=-2\lambda \end{cases}$

Pertanto la matrice A e la matrice A’ del sistema restano:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 1 \\[1.1ex] -1 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 1 & 2 -2\lambda \\[1.1ex] -1 & 2 & -2\lambda \end{array} \right)$

Infine, una volta trasformato il sistema, applichiamo la regola di Cramer . Per fare ciò, risolviamo prima il determinante di A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 \\[1.1ex] -1 & 2\end{vmatrix} =2-(-1)=3$

Per calcolare x con la regola di Cramer, cambiamo la prima colonna del determinante di A nella colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 -2\lambda & 1 \\[1.1ex] -2\lambda & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{4-4\lambda-(-2\lambda)}{3} = \cfrac{\bm{4-2\lambda}}{\bm{3}}$

Per calcolare y con la regola di Cramer, cambiamo la seconda colonna del determinante di A nella colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 2 -2\lambda \\[1.1ex] -1 & -2\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-2\lambda -(-2+2\lambda)}{3} = \cfrac{\bm{2-4\lambda} }{\bm{3}}$

Quindi quando m=2 la soluzione del sistema di equazioni è funzione di λ, poiché è uno SCI e quindi ha infinite soluzioni:

$\displaystyle \bm{x =} \cfrac{\bm{4-2\lambda}}{\bm{3}} \qquad \bm{y=}\cfrac{\bm{2-4\lambda}}{\bm{3}} \qquad \bm{z=\lambda}$

Abbiamo già analizzato la soluzione del sistema quando il parametro m è diverso da 2 e 3, e quando è uguale a 2. Ci serve quindi solo l’ultimo caso: quando m assume il valore 3:

m=3:

Analizzeremo ora cosa succede quando il parametro m è 3. In questo caso le matrici A e A’ sono:

$\displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 3 & 2 \\[1.1ex] 3 & 0 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 3 & 2 & 0 \\[1.1ex] 3 & 0 & 3 & 4 \end{array} \right)$

Come abbiamo visto in precedenza, quando m=3 il determinante di A è 0. Quindi la matrice A non è di rango 3. Ma al suo interno ha 2×2 determinanti diversi da 0, ad esempio:

$\displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 3 \end{vmatrix} = 3 - (-1)=4 \neq 0$

Quindi, in questo caso , il rango di A è 2 :

$\displaystyle rg(A)=2$

Una volta noto il rango della matrice A, calcoliamo il rango di A’. Il determinante delle prime 3 colonne dà 0, proviamo quindi un altro determinante 3×3 che sia interno alla matrice A’, ad esempio quello delle ultime 3 colonne:

$\displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 3 & 2 & 0 \\[1.1ex] 0 & 3 & 4\end{vmatrix}=2$

D’altra parte, la matrice A’ contiene un determinante il cui risultato è diverso da 0, quindi la matrice A’ è di rango 3 :

$\displaystyle rg(A')=3$

Pertanto, quando m = 3, il rango della matrice A è inferiore al rango della matrice A’. Quindi, dal teorema di Rouché-Frobenius, deduciamo che il sistema è un Sistema Incompatibile (SI) :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas}=3\end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A)=2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

Pertanto il sistema di equazioni non ha soluzione quando m = 3.

Riepilogo dell’esempio:

Come abbiamo visto, la soluzione del sistema di equazioni dipende dal valore del parametro m . Ecco il riepilogo di tutti i casi possibili:

m≠3 e m≠2:

$\displaystyle \bm{SCD} \longrightarrow \begin{cases} x = \cfrac{2m^2+8-8m}{m^2-5m+6} \\[3.5ex] y =\cfrac{-4+2m}{m^2-5m+6} \\[3.5ex] z = \cfrac{-2m+4}{m^2-5m+6} \end{cases}$

m=2:

$\displaystyle \bm{SCI} \longrightarrow \begin{cases} x = \cfrac{4-2\lambda}{3} \\[3.5ex] y= \cfrac{2-4\lambda}{3} \\[3.5ex] z = \lambda \end{cases}$

m=3:

$\displaystyle \bm{SI} \longrightarrow$

Il sistema non ha soluzione.

Qui abbiamo svolto l’intero procedimento utilizzando il teorema di Rouche e la regola di Cramer, ma i sistemi di equazioni con parametri possono anche essere discussi e risolti con il metodo di Gauss (con esercizi) . Puoi approfondire questo metodo nella pagina collegata, dove troverai una spiegazione dettagliata della procedura oltre ad esempi ed esercizi risolti passo dopo passo.

Problemi di discussione risolti di sistemi di equazioni lineari con parametri

Esercizio 1

Discuti e risolvi il seguente sistema di equazioni lineari dipendenti dai parametri:

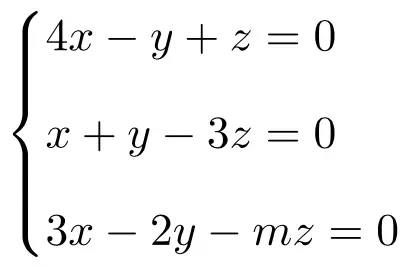
esercizio risolto di sistemi di equazioni con parametri

vedi soluzione

Per prima cosa realizziamo la matrice A e la matrice estesa A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)$

Dobbiamo ora trovare il rango della matrice A. Per fare ciò controlliamo se il determinante dell’intera matrice è diverso da 0:

$\displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{vmatrix} & =-4m+9-2-3-24-m \\ & =-5m-20 \end{aligned}$

Il risultato del determinante di A dipende dal valore di m. Vedremo quindi per quali valori di m il determinante svanisce. Per fare ciò, uguagliamo il risultato risultante a 0 e risolviamo l’equazione:

$-5m-20 = 0$

$-5m = 20$

$m = \cfrac{20}{-5} = -4$

Quindi, quando m è -4, il determinante di A sarà 0. E quando m è diverso da -4, il determinante di A sarà diverso da 0. Dobbiamo quindi analizzare ciascun caso separatamente:

m≠-4:

Come abbiamo appena visto, quando il parametro m è diverso da -4, il determinante della matrice A è diverso da 0. Pertanto il rango di A è 3.

$\displaystyle rg(A)=3$

Inoltre anche il rango della matrice A’ è 3, perché al suo interno c’è una sottomatrice 3×3 il cui determinante è diverso da 0. E non può essere di rango 4 poiché ‘non possiamo fare un determinante 4×4.

$\displaystyle rg(A')=3$

Pertanto, applicando il teorema di Rouché-Frobenius, sappiamo che questo è un sistema determinato compatibile (SCD), perché l’intervallo di A è uguale all’intervallo di A’ e al numero di incognite.

Una volta che sappiamo che il sistema è una SCD, applichiamo la regola di Cramer per risolverlo. Per fare ciò ricordiamo che la matrice A, il suo determinante e la matrice A’ sono:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)$

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m\end{vmatrix} =-5m-20$

Per calcolare xatex] con la regola di Cramer, sostituiamo la prima colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 0 & -1 & 1 \\[1.1ex] 0 & 1 & -3 \\[1.1ex] 0 & -2 & -m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}$

Per calcolare l’incognita e con la regola di Cramer, sostituiamo la seconda colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & 0 & 1 \\[1.1ex] 1 & 0 & -3 \\[1.1ex] 3 & 0 & -m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}$

Per calcolare z con la regola di Cramer, cambiamo la terza colonna del determinante di A nella colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}$

Pertanto, la soluzione del sistema di equazioni per il caso m≠-4 è:

x=0 y=0 z=0

m=-4:

Analizzeremo ora il sistema quando il parametro m è -4. In questo caso le matrici A e A’ sono:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & 4 & 0\end{array} \right)$

Come abbiamo visto in precedenza, quando m=-4 il determinante di A è 0. Quindi la matrice A non è di rango 3. Ma al suo interno ha 2×2 determinanti diversi da 0, ad esempio:

$\displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0$

Poiché la matrice ha un determinante di ordine 2 diverso da 0, la matrice A è di rango 2:

$\displaystyle rg(A)=2$

Una volta conosciuto il rango di A, calcoliamo il rango di A’. Sappiamo già che il determinante delle prime 3 colonne dà 0, quindi proviamo gli altri possibili determinanti 3×3:

$\displaystyle \begin{vmatrix} -1 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] -2 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] 3 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0\end{vmatrix} = 0$

Tutti i determinanti 3×3 della matrice A’ sono 0, quindi neanche la matrice A’ sarà di rango 3. Tuttavia, al suo interno ha determinanti di ordine 2 diversi da 0. Ad esempio:

$\displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0$

Quindi la matrice A’ sarà di rango 2:

$\displaystyle rg(A')=2$

L’estensione della matrice A è uguale all’estensione della matrice A’ ma queste due sono inferiori al numero di incognite nel sistema (3), quindi, secondo il teorema di Rouché-Frobenius, c è un Sistema Compatibile Indeterminato (ICS):

È un sistema ICS, quindi dobbiamo trasformare il sistema per risolverlo. Eliminiamo prima un’equazione, che in questo caso sarà l’ultima:

$\begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0 \\[1.5ex] \cancel{3x-2y+4z = 0} \end{cases} \longrightarrow \quad \begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0\end{cases}$

Ora convertiamo la variabile z in λ:

$\begin{cases}4x-y+z= 0 \\[1.5ex] x+y-3z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 4x-y+\lambda= 0 \\[1.5ex] x+y-3\lambda=0\end{cases}$

E mettiamo i termini con λ con i termini indipendenti:

$\begin{cases} 4x-y=-\lambda \\[1.5ex] x+y=3\lambda \end{cases}$

Tali che la matrice A e la matrice A’ del sistema rimangono:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 \\[1.1ex] 1 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 4 & -1 & -\lambda \\[1.1ex] 1 & 1 & 3\lambda \end{array} \right)$

Infine, una volta trasformato il sistema, applichiamo la regola di Cramer. Per fare ciò, risolviamo prima il determinante di A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} = 4-(-1)=5$

Per calcolare x con la regola di Cramer, cambiamo la prima colonna del determinante di A nella colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix}-\lambda & -1 \\[1.1ex] 3\lambda & 1 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-\lambda-(-3\lambda)}{5} =\cfrac{\bm{2\lambda}}{\bm{5}}$

Per calcolare l’incognita e con la regola di Cramer, sostituiamo la seconda colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & -\lambda \\[1.1ex] 1 & 3\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12\lambda-(-\lambda)}{5}=\cfrac{\bm{13\lambda}}{\bm{5}}$

Quindi quando m=-4 la soluzione del sistema di equazioni è funzione di λ, poiché è uno SCI e quindi ha infinite soluzioni:

$\displaystyle \bm{x =}\cfrac{\bm{2\lambda}}{\bm{5}}\qquad \bm{y=}\cfrac{\bm{13\lambda}}{\bm{5}} \qquad \bm{z=\lambda}$

Esercizio 2

Discuti e trova la soluzione del seguente sistema di equazioni lineari dipendenti dai parametri:

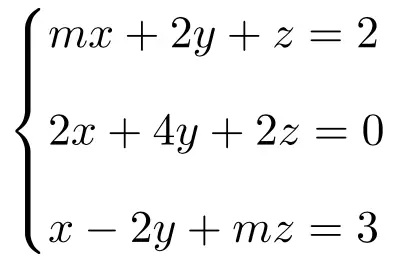
esercizio risolto passo dopo passo sistema di equazioni lineari con parametri

vedi soluzione

La prima cosa da fare è la matrice A e la matrice estesa A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}m & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & m & 3\end{array} \right)$

Dobbiamo ora trovare il rango della matrice A. Per fare ciò controlliamo se il determinante dell’intera matrice è diverso da 0:

$\displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix} & =4m^2+4-4-4+4m-4m \\ & =4m^2-4 \end{aligned}$

$4m^2-4 = 0$

$4m^2=4$

$m^2 = \cfrac{4}{4}$

$m^2 = 1$

$m = \pm 1$

Quindi, quando m è +1 o -1, il determinante di A sarà 0. E quando m è diverso da +1 e -1, il determinante di A sarà diverso da 0. Dobbiamo quindi analizzare ciascun caso mediante:

m≠+1 e m≠-1:

Come abbiamo appena visto, quando il parametro m è diverso da +1 e -1, il determinante della matrice A è diverso da 0. Pertanto il rango di A è 3.

$\displaystyle rg(A)=3$

$\displaystyle rg(A')=3$

Una volta che sappiamo che il sistema è una SCD, applichiamo la regola di Cramer per risolverlo. Per fare ciò ricordiamo che la matrice A, il suo determinante e la matrice A’ sono:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix}=4m^2-4$

Per calcolare x con la regola di Cramer, cambiamo la prima colonna del determinante di A nella colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2& 2 & 1 \\[1.1ex] 0 & 4 & 2 \\[1.1ex] 3 & -2 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{8m+8}}{\bm{4m^2-4}}$

Per calcolare l’incognita e con la regola di Cramer, sostituiamo la seconda colonna del determinante di A con la colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} m & 2 & 1 \\[1.1ex] 2 & 0 & 2 \\[1.1ex] 1 & 3 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{-10m+10}}{\bm{4m^2-4}}$

Per calcolare z con la regola di Cramer, cambiamo la terza colonna del determinante di A nella colonna dei termini indipendenti e la dividiamo per il determinante di A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix}m & 2 & 2 \\[1.1ex] 2 & 4 & 0 \\[1.1ex] 1 & -2 & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{12m-28}}{\bm{4m^2-4}}$

Pertanto, la soluzione del sistema di equazioni per il caso m≠+1 e m≠-1 è:

$\displaystyle \bm{x = }\cfrac{\bm{8m+8}}{\bm{4m^2-4}} \qquad \bm{y=}\cfrac{\bm{-10m+10}}{\bm{4m^2-4}}\qquad \bm{z =} \cfrac{\bm{12m-28}}{\bm{4m^2-4}}$

m=+1:

Analizzeremo ora il sistema quando il parametro m è uguale a 1. In questo caso le matrici A e A’ sono:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & 1 & 3\end{array} \right)$

Come abbiamo visto in precedenza, quando m=+1 il determinante di A è 0. Quindi la matrice A non è di rango 3. Ma al suo interno ha 2×2 determinanti diversi da 0, ad esempio:

$\displaystyle \begin{vmatrix}2 & 4\\[1.1ex] 1 & -2 \end{vmatrix} =-4-4=-8 \neq 0$

Poiché la matrice ha un determinante di ordine 2 diverso da 0, la matrice A è di rango 2:

$\displaystyle rg(A)=2$

Una volta conosciuto il rango di A, calcoliamo il rango di A’. Sappiamo già che il determinante delle prime 3 colonne dà 0, quindi ora proviamo, ad esempio, con il determinante delle ultime 3 colonne:

$\displaystyle \begin{vmatrix} 2 & 1 & 2 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -2 & 1 & 3 \end{vmatrix} = 16$

D’altra parte, la matrice A’ contiene un determinante 3×3 il cui risultato è diverso da 0, quindi la matrice A’ è di rango 3:

$\displaystyle rg(A')=3$

Pertanto, quando m=+1 il rango della matrice A è inferiore al rango della matrice A’. Quindi, dal teorema di Rouché-Frobenius, deduciamo che il sistema è un Sistema Incompatibile (SI):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

Pertanto il sistema di equazioni non ha soluzione quando m=+1 , poiché è un sistema incompatibile.

m=-1:

Analizzeremo ora il sistema quando il parametro m è -1. In questo caso le matrici A e A’ sono:

$\displaystyle A= \left( \begin{array}{ccc} -1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}-1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & -1 & 3\end{array} \right)$

Come abbiamo visto in precedenza, quando m=-1 il determinante di A è 0. Quindi la matrice A non è di rango 3. Ma al suo interno ha 2×2 determinanti diversi da 0, ad esempio:

$\displaystyle \begin{vmatrix}-1 & 2\\[1.1ex] 2 & 4 \end{vmatrix} =-4-4=-8 \neq 0$

Poiché la matrice ha un determinante di ordine 2 diverso da 0, la matrice A è di rango 2:

$\displaystyle rg(A)=2$

$\displaystyle \begin{vmatrix} -1 & 1 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 1 & -1 & 3\end{vmatrix} = -20$

D’altra parte, la matrice A’ contiene un determinante 3×3 il cui risultato è diverso da 0, quindi la matrice A’ è di rango 3:

$\displaystyle rg(A')=3$

Pertanto, quando m = -1, il rango della matrice A è inferiore al rango della matrice A’. Quindi, dal teorema di Rouché-Frobenius, deduciamo che il sistema è un Sistema Incompatibile (SI):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

Pertanto il sistema di equazioni non ha soluzione quando m=-1 , poiché è un sistema incompatibile.

Discussione di sistemi di equazioni con parametri

Esempio di sistema di equazioni lineari con parametri

Riepilogo dell’esempio:

Problemi di discussione risolti di sistemi di equazioni lineari con parametri

Esercizio 1

Esercizio 2

Lascia un commento Annulla risposta