In questo articolo imparerai come studiare la differenziabilità di una funzione, cioè se una funzione è differenziabile o meno. Inoltre, vedremo la relazione tra differenziabilità e continuità di una funzione. Infine studieremo la differenziabilità di una funzione a tratti.
Differenziabilità e continuità di una funzione
La continuità e la differenziabilità di una funzione in un punto sono correlate come segue:
- Se una funzione è differenziabile in un punto, in quel punto la funzione è continua.
- Se una funzione non è continua in un punto, in quel punto non è nemmeno differenziabile.
Tuttavia, il contrario di questo teorema è falso: solo perché una funzione è continua in un punto non significa che sia sempre differenziabile in quel punto.
Puoi anche vedere se una funzione è differenziabile o meno in un punto dalla sua rappresentazione grafica:
- Se è un punto liscio, la funzione a questo punto è differenziabile.
- Se è un punto angolare, la funzione è continua ma non differenziabile in questo punto.

Punto di livellamento a x=0:
funzione continua e differenziabile in questa fase.

Punto angolare in x=2:
funzione continua ma non differenziabile in questa fase.
Differenziabilità di una funzione a tratti
Una volta conosciuta la relazione tra continuità e differenziabilità di una funzione, vedremo come studiare la differenziabilità di una funzione definita a tratti.
Puoi capire se una funzione a tratti è differenziabile in un punto calcolando le derivate laterali in quel punto:
- Se le derivate laterali in un punto non sono uguali, la funzione in quel punto non è differenziabile:
![]()
Non è deducibile
![]()
- Se le derivate laterali in un punto coincidono, la funzione in quel punto è differenziabile:
![]()
Sì, è differenziabile in
![]()
Nota: affinché una funzione sia differenziabile in un punto, la funzione deve essere continua in quel punto. Pertanto, prima di calcolare le derivate laterali, dobbiamo assicurarci che la funzione sia continua in quel punto. Se non sai come si studia la continuità in un punto, puoi vedere come si fa nel seguente link:
Vediamo ora un esempio di come calcolare la derivata di una funzione definita a tratti in un punto:
- Studia la continuità e la differenziabilità della seguente funzione definita a tratti nel punto x=2:
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} 3x^2-6x & \text{si} & x<2 \\[2ex] 6\ln (x-1) & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-a98eee72521c68fd394eb6209a7d0a59_l3.png)
Le funzioni delle due parti sono continue nei rispettivi intervalli, occorre però vedere se la funzione è continua nel punto critico x=2. Per fare ciò risolviamo i limiti laterali della funzione nel punto:
![]()
![]()
I limiti laterali nel punto critico ci hanno dato lo stesso risultato, quindi la funzione è continua nel punto x=2.
Una volta che sappiamo che la funzione è continua in x=2, studieremo la differenziabilità della funzione in quel punto. Per fare ciò, calcoliamo le derivate laterali della funzione definita in pezzi:
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 6x-6 & \text{si} & x<2 \\[2ex] \cfrac{6}{x-1} & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3709995609d0f69f382ff651e397c00a_l3.png)
Valutiamo ora ciascuna derivata laterale nel punto critico:
![]()
![]()
Le due derivate laterali ci hanno dato lo stesso risultato, quindi la funzione è differenziabile in x=2 e il valore della derivata è 6:
![]()
D’altra parte, se le derivate laterali ci avessero dato un risultato diverso, ciò significherebbe che la funzione non è differenziabile in x=2. In altre parole, a questo punto la derivata non esisterebbe.
Ricordiamo infine che questa procedura è valida anche per studiare la differenziabilità di una funzione a valore assoluto, poiché le funzioni a valore assoluto possono essere definite anche a tratti. Puoi vedere come convertire una funzione di valore assoluto in blocchi qui:
➤ Vedi: come definire a tratti una funzione con valore assoluto
Esercizi risolti sulla differenziabilità di una funzione
Esercizio 1
Studiare la continuità e la differenziabilità della seguente funzione a tratti:
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} x^3-4x^2 + 5 & \text{si} & x<1 \\[2ex] -x^2+3x & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3656065bb8de98bd07da153f26fd326e_l3.png)
Le funzioni delle due parti sono continue, ma dobbiamo vedere se la funzione è continua nel punto critico x=1. Per fare questo risolviamo i limiti laterali della funzione nel punto:
![]()
![]()
I due limiti laterali nel punto critico danno lo stesso risultato, quindi la funzione è continua in x=1.
Una volta che sappiamo che la funzione è continua nel punto critico, studieremo se è differenziabile nello stesso punto. Calcoliamo quindi le derivate laterali:
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 3x^2-8x & \text{si} & x<1 \\[2ex] -2x+3 & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-42451fa799527167fe9a2e2259248870_l3.png)
E valutiamo le due derivate laterali in x=1;
![]()
![]()
Le derivate laterali non coincidono nel punto x=1 quindi la funzione non è differenziabile in questo punto.
![]()
Esercizio 2
Analizzare la differenziabilità e la continuità della seguente funzione definita nelle sezioni:
![\displaystyle f(x)= \left\{ \begin{array}{lcl} \sqrt{4x} & \text{si} & x\leq 1 \\[2ex] 2+\ln x & \text{si} & x> 1 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”226″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-0d118e3904c810abd15e427e9c7d0504_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} \cfrac{4}{2\sqrt{4x}} & \text{si} & x<1 \\[4ex] \cfrac{1}{x} & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-8261f3d268b47d9171710997c8cc70bd_l3.png)
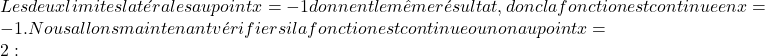
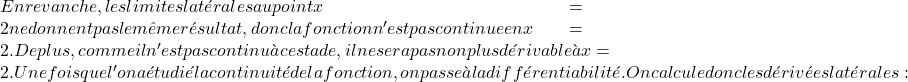
^2 & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce34d5d8a949fb3a0b904e9bf7d32f5b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 2e^{x-3} & \text{si} & x< 3 \\[2ex]2(x-b) & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-d542fc9488644f0c144059ae1403d961_l3.png)