In questa pagina imparerai qual è il determinante di una matrice quadrata 3×3. Vedrai come risolvere le determinanti dell’ordine 3 utilizzando la regola di Sarrus. E, inoltre, hai esempi ed esercizi risolti passo dopo passo, così puoi esercitarti e capirlo perfettamente.
Qual è il determinante di una matrice 3×3?
Un determinante di ordine 3 è una matrice di dimensione 3×3 rappresentata da una barra verticale su ciascun lato della matrice. Se ad esempio abbiamo la seguente matrice:
![\displaystyle A = \begin{pmatrix} 2 & 0 & 4 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 1 & 6 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7b5e89b706893e88dd15882e3685afb1_l3.png "Rendered by QuickLaTeX.com")
Il determinante della matrice A è rappresentato come segue:
![\displaystyle \lvert A \rvert = \begin{vmatrix} 2 & 0 & 4 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 1 & 6 & -2 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41db04327de87a80f1e0e4dd6dcb220a_l3.png "Rendered by QuickLaTeX.com")
Come hai visto, scrivere il determinante di una matrice quadrata di ordine 3 è facile. Ora vediamo come risolverlo:
Come calcolare un determinante di ordine 3?
Per ricavare i determinanti delle matrici 3×3 bisogna applicare la regola di Sarrus :
Regola Sarrus
La regola di Sarrus dice che per calcolare un determinante di ordine 3 bisogna sommare il prodotto degli elementi della diagonale maggiore e il prodotto delle sue diagonali parallele con i corrispondenti vertici opposti, quindi sottrarre il prodotto degli elementi della diagonale minore e il prodotto delle loro diagonali parallele con i corrispondenti vertici opposti.
Scritto così può essere un po’ difficile da capire, ma guarda come viene eseguito il calcolo dei determinanti 3×3 con il seguente diagramma ed esempi:
Esempi di determinanti 3×3:
![\begin{aligned} \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] -1 & 1 & 0 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} & = 2 \cdot 1 \cdot 1 + 1 \cdot 0 \cdot (-2) + (-1) \cdot 4 \cdot 3 - (-2) \cdot 1 \cdot 3 - 4 \cdot 0 \cdot 2- (-1) \cdot 1 \cdot 1 \\ & = 2 + 0 -12 +6 - 0 +1 \\[2ex] & = \bm{-3} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-98e60cf465cd0eb7662d47770cd38231_l3.png "Rendered by QuickLaTeX.com")
![\begin{aligned} \begin{vmatrix} 1 & 0 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 4 & -3 & -1 \end{vmatrix} & = 1\cdot 2 \cdot (-1) + 0 \cdot 1 \cdot 4 +3 \cdot (-3) \cdot 2 - 4 \cdot 2 \cdot 2 - (-3) \cdot 1 \cdot 1- 3 \cdot 0 \cdot (-1) \\ & = -2 +0 -18 - 16 +3- 0 \\[2ex] & = \bm{-33} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41a53c1fd6eae1b51a280a6ce1e2ab91_l3.png "Rendered by QuickLaTeX.com")
Risolti problemi di determinanti di matrici 3 × 3
Esercizio 1
Risolvi il seguente determinante 3×3:
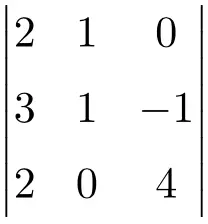
Per risolvere il determinante di una matrice 3×3 dobbiamo applicare la regola di Sarrus:
![\displaystyle\begin{aligned} \begin{vmatrix} 2 & 1 & 0 \\[1.1ex] 3 & 1 & -1 \\[1.1ex] 2 & 0 & 4 \end{vmatrix} & = 2 \cdot 1 \cdot 4 + 1 \cdot (-1) \cdot 2 + 3 \cdot 0 \cdot 0 - 2 \cdot 1 \cdot 0 - 0 \cdot (-1) \cdot 2- 3 \cdot 1 \cdot 4 \\ & = 8 -2 +0 -0- 0-12 \\[2ex] & = \bm{-6} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8f288312b72f3bbabc35ee64bf580d8c_l3.png "Rendered by QuickLaTeX.com")
Esercizio 2
Calcolare il seguente determinante di ordine 3:
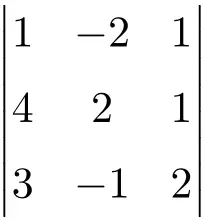
Per calcolare il determinante di una matrice del terzo ordine dobbiamo utilizzare la regola di Sarrus:
![\displaystyle\begin{aligned} \begin{vmatrix} 1 & -2 & 1 \\[1.1ex] 4 & 2 & 1 \\[1.1ex] 3 & -1 & 2 \end{vmatrix} & = 1 \cdot 2 \cdot 2 + (-2) \cdot 1 \cdot 3 + 4 \cdot (-1) \cdot 1 - 3 \cdot 2 \cdot 1 - (-1) \cdot 1 \cdot 1 - 4 \cdot (-2) \cdot 2 \\ & = 4 -6 -4 -6+1+16 \\[2ex] & = \bm{5} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-64078968233ec50d2e793309d55e55fc_l3.png "Rendered by QuickLaTeX.com")
Esercizio 3
Trova la soluzione del determinante della seguente matrice 3×3:
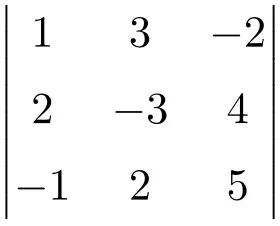
Per creare un determinante di una matrice 3×3, dobbiamo utilizzare la regola di Sarrus:
![\displaystyle\begin{aligned} \begin{vmatrix}1 & 3 & -2 \\[1.1ex] 2 & -3 & 4 \\[1.1ex] -1 & 2 & 5 \end{vmatrix} & = \\ & = 1 \cdot (-3) \cdot 5 + 3 \cdot 4 \cdot (-1) + 2 \cdot 2 \cdot (-2) \ - \\[1.1ex] & \phantom{=} - (-1) \cdot (-3) \cdot (-2) - 2 \cdot 4 \cdot 1 - 2 \cdot 3 \cdot 5 \\[2.5ex] & = -15 -12 -8 +6-8-30 \\[2.5ex] & = \bm{-67} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fd4494ae66a604834b8f9f47fcbbe41d_l3.png "Rendered by QuickLaTeX.com")
Esercizio 4
Trova la soluzione del determinante della seguente matrice di ordine 3:
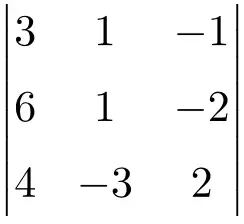
Per trovare la soluzione di un determinante di una matrice 3×3 dobbiamo applicare la formula di Sarrus:
![\displaystyle\begin{aligned} \begin{vmatrix} 3 & 1 & -1 \\[1.1ex] 6 & 1 & -2 \\[1.1ex] 4 & -3 & 2 \end{vmatrix} & = \\ & = 3 \cdot 1 \cdot 2 + 1 \cdot (-2) \cdot 4 + 6 \cdot (-3) \cdot (-1) \ - \\[1.1ex] & \phantom{=} - 4 \cdot 1 \cdot (-1) - (-3) \cdot (-2) \cdot 3 - 6 \cdot 1 \cdot 2 \\[2.5ex] & =6 -8 +18 +4-18-12 \\[2.5ex] & = \bm{-10} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e811024d460a60a1df59983b1f700e8_l3.png "Rendered by QuickLaTeX.com")
Esercizio 5
trovare il valore di
che annulla il seguente determinante del terzo ordine:
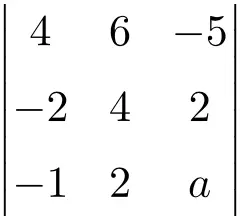
Calcoliamo innanzitutto, con la regola di Sarrus, il valore del determinante in funzione di
![\displaystyle\begin{aligned}\begin{vmatrix} 4 & 6 & -5 \\[1.1ex] -2 & 4 & 2 \\[1.1ex] -1 & 2 & a \end{vmatrix} & = \\ & = 4 \cdot 4 \cdot a + 6 \cdot 2 \cdot (-1) + (-2) \cdot 2 \cdot (-5) \ - \\[1.1ex] & \phantom{=}- (-1) \cdot 4 \cdot (-5) - 2 \cdot 2 \cdot 4 - (-2) \cdot 6 \cdot a \\[2.5ex] & = 16a -12 + 20 - 20 - 16 +12a \\[2.5ex] & = 28a -28 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-07e67cfc5e45c0a11c35d643cd4c1c78_l3.png "Rendered by QuickLaTeX.com")
Perché il determinante scompaia, il risultato deve essere 0. Pertanto, impostiamo il risultato uguale a 0 e risolviamo l’equazione:
