Come calcolare il determinante di una matrice 2×2

In questa pagina imparerai qual è il determinante di una matrice 2×2. Inoltre, troverai esempi ed esercizi risolti passo dopo passo su come risolvere i determinanti dell’ordine 2, così potrai esercitarti e comprenderlo perfettamente.

Cos’è un determinante 2×2?

Un determinante di ordine 2 è una matrice di dimensione 2 × 2 rappresentata da una barra verticale su ciascun lato della matrice. Se ad esempio abbiamo la seguente matrice:

\displaystyle A = \begin{pmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}

Il determinante della matrice A è rappresentato come segue:

\displaystyle \lvert A \rvert = \begin{vmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{vmatrix}

Come hai visto, scrivere il determinante di una matrice quadrata 2×2 è facile. Ora vediamo come viene calcolato:

Come risolvere un determinante di ordine 2?

Per calcolare il determinante di una matrice 2×2 dobbiamo moltiplicare gli elementi della diagonale principale e sottrarre il prodotto della diagonale secondaria.

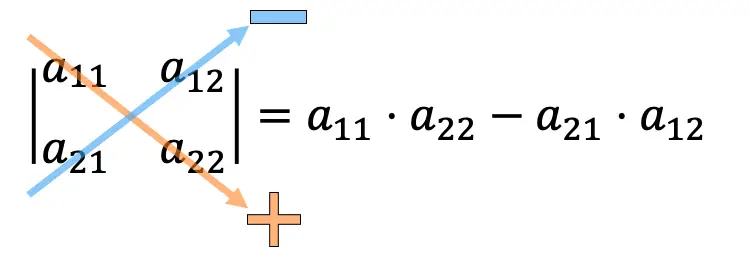
esempio di calcolo del determinante di una matrice 2x2

Esempi di calcolo dei determinanti 2×2:

\displaystyle\begin{vmatrix} 3 & 4 \\[1.1ex] 2 & 1 \end{vmatrix} = 3 \cdot 1 - 2 \cdot 4 = 3 - 8 = \bm{-5}

\displaystyle\begin{vmatrix} 2 & -3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot (-3) =10-(-3) = 10+3= \bm{13}

Risolti problemi di determinanti di matrici 2 × 2

Esercizio 1

Calcolare il seguente determinante 2×2:

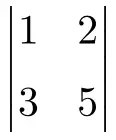
esercizio risolto passo passo del determinante 2x2

Per creare un determinante 2×2, devi moltiplicare gli elementi della diagonale principale e sottrarre il prodotto della diagonale secondaria:

\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 3 & 5 \end{vmatrix} = 1 \cdot 5 - 3 \cdot 2 = 5 - 6 = \bm{-1}

Esercizio 2

Risolvi il seguente determinante della dimensione 2×2:

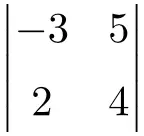
esercizi risolti passo dopo passo sui determinanti 2x2

Per trovare la soluzione di un determinante di ordine 2, devi moltiplicare gli elementi della diagonale principale e sottrarre il prodotto della diagonale secondaria:

\displaystyle \begin{vmatrix} -3 & 5 \\[1.1ex] 2 & 4 \end{vmatrix} = -3 \cdot 4 - 2 \cdot 5 = -12 - 10 = \bm{-22}

Esercizio 3

Trovare la soluzione del seguente determinante di ordine 2:

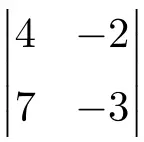
esercizio risolto passo passo di un determinante di una matrice 2x2

Per trovare la soluzione di un determinante di dimensione 2, devi moltiplicare gli elementi della diagonale principale e sottrarre il prodotto della diagonale secondaria:

\displaystyle \begin{vmatrix} 4 & -2 \\[1.1ex] 7 & -3\end{vmatrix} = 4 \cdot (-3) - 7 \cdot (-2) = -12 - (-14) =-12+14= \bm{2}

Esercizio 4

Calcolare il seguente determinante 2×2:

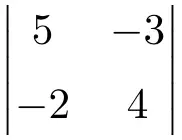
come risolvere il determinante di una matrice 2x2, esercizio risolto passo dopo passo

Per calcolare i determinanti delle matrici 2×2, dobbiamo moltiplicare gli elementi della diagonale principale e sottrarre il prodotto della diagonale secondaria:

\displaystyle \begin{vmatrix} 5 & -3 \\[1.1ex] -2 & 4\end{vmatrix} = 5 \cdot 4 - (-2) \cdot (-3) = 20 - (+6) = \bm{14}

Esercizio 5

Determinare il risultato del seguente determinante 2×2:

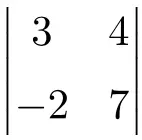
Esercizio risolto sulla risoluzione passo passo del determinante di una matrice di ordine 2

Per trovare la soluzione di un determinante 2×2 dobbiamo moltiplicare gli elementi della diagonale principale e sottrarre il prodotto della diagonale secondaria:

\displaystyle \begin{vmatrix} 3 & 4 \\[1.1ex] -2 & 7\end{vmatrix} = 3 \cdot 7 - (-2) \cdot 4 = 21 - (-8)=21+8 = \bm{29}

Luminoso! Ora sai come creare determinanti della dimensione 2×2! Ora sicuramente sei già in grado di capire come si calcola il determinante 3×3 e anche come si risolve il determinante di una matrice 4×4 .

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *

Torna in alto