Derivato da una radice: Mathority

Qui spieghiamo come derivare una radice (o una funzione radicale). Troverai la formula per dividere le radici e gli esercizi risolti passo passo per le derivate delle radici.

Formula per la derivata di una radice

La derivata di una radice, o funzione irrazionale, è uguale alla derivata del radicando (espressione sotto il radicale) divisa per il prodotto dell’indice della radice per la radice stessa, sottraendo 1 dall’esponente del radicando.

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

Tuttavia, se il radicando radice è solo una x, le formule si semplificano. La derivata radice di x è quindi la seguente:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

In breve, ci sono due formule per derivare una radice: la prima che può essere usata sempre e la seconda che può essere usata solo quando il radicando è x.

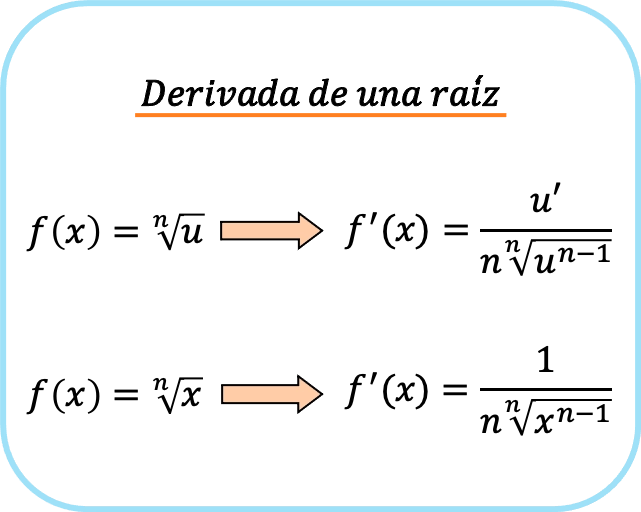
Se guardi da vicino, il termine al numeratore della frazione è quello che risulta dall’applicazione della regola della catena quando si prende la derivata della radice. Questo è il motivo per cui quando il radicando è x, 1 appare al denominatore poiché è la derivata di x.

Esempi di derivati delle radici

Data la formula per la derivata di una funzione radicale, di seguito spieghiamo alcuni esempi di questo tipo di derivata in modo che tu possa capire come derivare di una radice.

Esempio 1: derivata di una radice quadrata

Vedremo poi qual è la derivata di una radice quadrata:

$f(x)=\sqrt{x}$

In questo caso, l’espressione all’interno della radice è solo una x, quindi possiamo usare la seguente formula:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Quindi la derivata di una radice quadrata è uguale a 1 diviso per il prodotto di 2 volte la radice quadrata di x:

$f(x)=\sqrt{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{2\sqrt{x^{2-1}}}=\cfrac{1}{2\sqrt{x}}$

Esempio 2: Derivazione di una radice cubica

$f(x)=\sqrt[3]{x}$

In questo esempio, l’espressione sotto la radice è una x, quindi possiamo applicare la seguente formula:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Quindi la derivata di una radice cubica è uguale a 1 diviso per 3 volte la radice cubica di x al quadrato:

$f(x)=\sqrt[3]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{3\sqrt[3]{x^{3-1}}}=\cfrac{1}{3\sqrt[3]{x^2}}$

Esempio 3: Derivata di una radice quarta

$f(x)=\sqrt[4]{7x-2}$

Ora non abbiamo una x sotto il segno radicale, ma abbiamo un’espressione algebrica più complessa. Dobbiamo quindi utilizzare la formula generale per la derivata di una radice:

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

L’espressione sotto il radicale è una funzione di primo grado, quindi la sua derivata è 7. Pertanto, la derivata dell’intera funzione è:

$f(x)=\sqrt[4]{7x-2}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{7}{4\sqrt[4]{(7x-2)^3}}$

Esempio 4: Derivazione da una radice all’altra

$f(x)=\sqrt{x^2+\sqrt[3]{x^4-5}}$

Per risolvere la derivata di questa radice composta da un’altra radice, dobbiamo applicare la seguente formula:

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

In questo caso, devi utilizzare la stessa formula due volte consecutive per calcolare la derivata:

$\begin{aligned}f'(x)& =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot\left(x^2+\sqrt[3]{x^4-5}\right)' \\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot (x^4-5)'\right)\\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot 4x^3\right)\end{aligned}$

Risolti problemi della derivata di una radice

Calcolare le derivate delle seguenti radici:

$\text{A) } f(x)=\sqrt[5]{x}$

$\text{B) } f(x)=\sqrt[3]{x^4}$

$\text{C) } f(x)=\sqrt{x^2-4x+9}$

$\text{D) } f(x)=\sqrt[4]{x^9+5x^4-2x}$

$\text{E) } f(x)=\sqrt[5]{3(x^2-1)^4}$

$\text{F) } f(x)=\sqrt[6]{x^2+4(5x^3-8x)^2}$

vedi soluzione

$\text{A) } f'(x)=\cfrac{1}{5\sqrt[5]{x^4}}$

$\text{B) } f'(x)=\cfrac{4x^3}{3\sqrt[3]{\left(x^4\right)^2}}= \cfrac{4x^3}{3\sqrt[3]{x^8}}$

$\text{C) } f'(x)=\cfrac{2x-4}{2\sqrt{x^2-4x+9}}$

$\text{D) } f'(x)=\cfrac{9x^8+20x^3-2}{4\sqrt[4]{\left(x^9+5x^4-2x\right)^3}}$

$\text{E) } f'(x)=\cfrac{3\cdot 4 \cdot (x^2-1)^3\cdot 2x}{5\sqrt[5]{\left(3\left(x^2-1\right)^4\right)^4}}=\cfrac{24x(x^2-1)^3}{5\sqrt[5]{81\left(x^2-1\right)^{16}}}$

$\text{F) } f'(x)=\cfrac{2x+2\cdot 4(5x^3-8x)\cdot (15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}=\cfrac{2x+8(5x^3-8x)(15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}$

Formula per la derivata di una radice

Esempi di derivati delle radici

Esempio 1: derivata di una radice quadrata

Esempio 2: Derivazione di una radice cubica

Esempio 3: Derivata di una radice quarta

Esempio 4: Derivazione da una radice all’altra

Risolti problemi della derivata di una radice

Lascia un commento Annulla risposta