In questa pagina vedrai qual è la derivata dell’arco coseno iperbolico (formula). Troverai anche esercizi risolti passo passo per le derivate dell’arcocoseno iperbolico di una funzione. E, infine, troverai la dimostrazione della formula per la derivata di questo tipo di funzione trigonometrica.
Formula per la derivata dell’arco coseno iperbolico
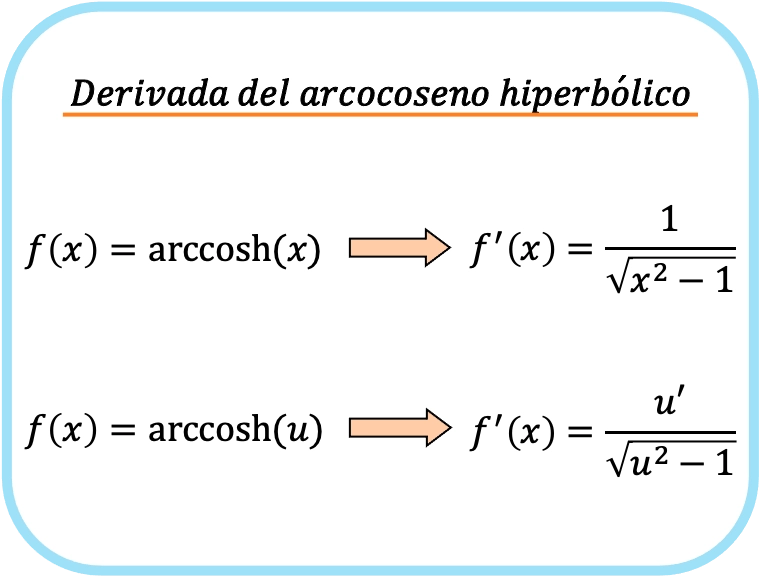
La derivata dell’arcocoseno iperbolico di x è uno fratto la radice quadrata di x al quadrato meno 1.
![]()
Pertanto, la derivata dell’arco coseno iperbolico di una funzione è uguale al quoziente della derivata di quella funzione diviso per la radice quadrata di quella funzione al quadrato meno uno.
![]()
La seconda formula include la regola della catena e quindi può essere utilizzata per derivare qualsiasi arcocoseno iperbolico. Infatti, se sostituiamo la u con la x, otterremo la prima formula. La prima formula, invece, funziona solo per la derivata arcocoseno iperbolica di x.
L’arcocoseno iperbolico è la funzione inversa del coseno iperbolico e quindi le due funzioni sono correlate. Puoi vedere la formula per la derivata di questa funzione trigonometrica cliccando qui:
➤ Vedi: formula per la derivata del coseno iperbolico
Esempi di derivata dell’arcoseno iperbolico
Esempio 1
![]()
Per trovare la derivata dell’arcocoseno iperbolico dobbiamo utilizzare la formula corrispondente, che è:
![]()
Pertanto, al numeratore della frazione dobbiamo mettere la derivata di 5x, che è 5. E al denominatore dobbiamo solo mettere la radice quadrata della funzione argomento al quadrato meno 1:
![]()
Esempio 2
![]()
La funzione che si ricava da questo esercizio è un arcocoseno iperbolico, quindi per ricavarla utilizziamo la seguente formula:
![]()
Pertanto, al numeratore scriviamo la derivata dell’argomento della funzione e al denominatore la radice quadrata della funzione dell’argomento elevata a 2 meno 1:
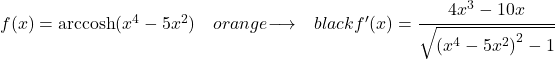
Dimostrazione della derivata dell’arco coseno iperbolico
Infine, dimostreremo la formula per la derivata dell’arco coseno iperbolico.
![]()
Per prima cosa trasformiamo l’arco coseno iperbolico in un coseno iperbolico:
![]()
Deduciamo da entrambi i lati dell’uguaglianza:
![]()
Ti chiariamo:
![]()
Usiamo ora l’identità trigonometrica che mette in relazione il seno iperbolico e il coseno iperbolico per modificare il denominatore:
![]()
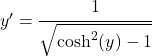
Tuttavia, prima abbiamo dedotto che x è equivalente al coseno iperbolico di y, quindi l’equazione rimane:
![]()