Derivato dell'arcoseno

In questo articolo spieghiamo come ricavare l’arcoseno di una funzione. Troverai esempi di derivate dell’arcoseno di funzioni e potrai anche esercitarti con esercizi risolti passo dopo passo. Infine, vedrai anche la dimostrazione della formula della derivata dell’arcoseno.

Qual è la derivata dell’arcoseno?

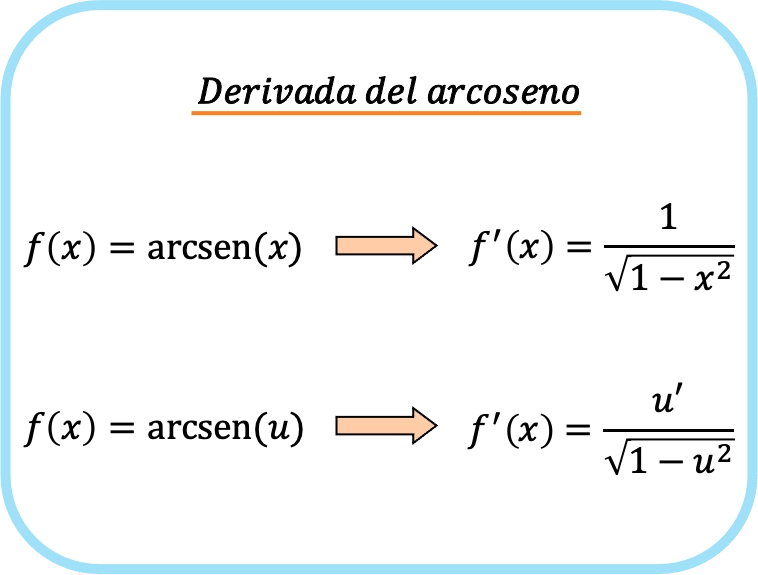
La derivata arcoseno di x è uno fratto la radice quadrata di uno meno x al quadrato.

$f(x)=\text{arcsen}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{\sqrt{1-x^2}}$

Pertanto, la derivata dell’arcoseno di una funzione è uguale al quoziente della derivata di quella funzione diviso per la radice quadrata di uno meno la funzione al quadrato.

$f(x)=\text{arcsen}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{1-u^2}}$

Logicamente, la seconda formula si ottiene applicando la regola della catena alla prima formula.

Ricorda che l’arcoseno è la funzione inversa del seno, motivo per cui è anche chiamato seno inverso.

Esempi di derivata dell’arcoseno

Dopo aver visto qual è la formula della derivata dell’arcoseno, spiegheremo alcuni esempi di questo tipo di derivate trigonometriche. In questo modo ti sarà più semplice capire come si ricava l’arcoseno di una funzione.

Esempio 1: Derivata dell’arcoseno di 2x

$f(x)=\text{arcsen}(2x)$

Per trovare la derivata della funzione arcoseno dobbiamo utilizzare la formula corrispondente:

$f(x)=\text{arcsen}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{1-u^2}}$

Quindi la derivata di 2x è 2, quindi la derivata arcoseno di 2x è 2 diviso per la radice di uno meno 2x al quadrato:

$f(x)=\text{arcsen}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{\sqrt{1-(2x)^2}}=\cfrac{2}{\sqrt{1-4x^2}}$

Esempio 2: Derivata dell’arcoseno di x al quadrato

$f(x)=\text{arcsen}(x^2)$

Usiamo la formula della derivata dell’arcoseno per ricavarlo:

$f(x)=\text{arcsen}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{1-u^2}}$

La funzione ^x2 è di secondo grado, quindi la sua derivata è 2x. Pertanto la derivata dell’arcoseno di x elevata alla potenza di 2 è:

$f(x)=\text{arcsen}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{\sqrt{1-\left(x^2\right)^2}}=\cfrac{2x}{\sqrt{1-x^4}}$

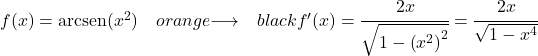
Esempio 3: Derivata dell’arcoseno di e ^x

$f(x)=\text{arcsen}(e^x)$

La funzione in questo esempio è una funzione composta, quindi dobbiamo applicare la regola della catena per risolvere la derivata:

$f(x)=\text{arcsen}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{1-u^2}}$

La derivata di e ^x è essa stessa, quindi la derivata dell’intera funzione è:

$f(x)=\text{arcsen}(e^x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{e^x}{\sqrt{1-\left(e^x\right)^2}}=\cfrac{e^x}{\sqrt{1-e^{2x}}}$

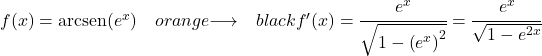
Problemi risolti con la derivata dell’arcoseno

Derivare le seguenti funzioni arcoseno:

$\text{A) }f(x)=\text{arcsen}(6x)$

$\text{B) }f(x)=\text{arcsen}(x^2-4x)$

$\text{C) }f(x)=\text{arcsen}\left(3x^4-6x^3+9+e^{x^2}\right)$

$\text{D) }f(x)=\text{arcsen}\left(\log_5(3x)\right)$

$\text{E) }f(x)=\text{arcsen}\left(\sqrt{4x}\right)$

vedi soluzione

$\text{A) }f'(x)=\cfrac{6}{\sqrt{1-(6x)^2}}=\cfrac{6}{\sqrt{1-36x^2}}$

$\text{B) }f'(x)=\cfrac{2x-4}{\sqrt{1-(x^2-4x)^2}}$

$\text{C) }f'(x)=\cfrac{12x^3-18x^2+2x\cdot e^{x^2}}{\sqrt{1-(3x^4-6x^3+9+e^{x^2})^2}}$

$\text{D) }f'(x)=\cfrac{1}{\sqrt{1-\left(\log_5(3x)\right)^2}}\cdot \cfrac{3}{3x\cdot \ln 5}=\cfrac{1}{x\cdot \ln 5\cdot \sqrt{1-\left(\log_5(3x)\right)^2}}$

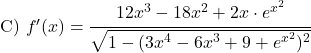
$\begin{aligned}\text{E) } f'(x)& =\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}$

Dimostrazione della formula del derivato dell’arcoseno

Successivamente, procediamo alla dimostrazione matematica della formula per la derivata dell’arcoseno.

$y=\text{arcsen}(x)$

Per prima cosa trasformiamo l’arcoseno in seno:

$x=\text{sen}(y)$

Ora differenziamo entrambi i lati dell’equazione:

$1=\text{cos}(y)\cdot y'$

Ti chiariamo:

$y'=\cfrac{1}{\text{cos}(y)}$

Successivamente, applichiamo l’identità trigonometrica fondamentale:

$\text{sen}^2(y)+\text{cos}^2(y)=1 \ \longrightarrow \ \text{cos}(y)=\sqrt{1-\text{sen}^2(y)}$

$y'=\cfrac{1}{\sqrt{1-\text{sen}^2(y)}}$

E, poiché abbiamo dedotto sopra che x era equivalente al seno di y, l’uguaglianza rimane:

$y'=\cfrac{1}{\sqrt{1-x^2}}$

Come puoi vedere, applicando questa procedura abbiamo ottenuto la formula per la derivata della funzione arcoseno, quindi è dimostrato che la formula è soddisfatta.

Qual è la derivata dell’arcoseno?

Esempi di derivata dell’arcoseno

Esempio 1: Derivata dell’arcoseno di 2x

Esempio 2: Derivata dell’arcoseno di x al quadrato

Esempio 3: Derivata dell’arcoseno di e x

Problemi risolti con la derivata dell’arcoseno

Dimostrazione della formula del derivato dell’arcoseno

Lascia un commento Annulla risposta

Esempio 3: Derivata dell’arcoseno di e ^x