Derivato dell'arcocoseno

Qui spieghiamo come derivare l’arcocoseno di una funzione. Inoltre troverai esempi di derivate dell’arcocoseno e potrai esercitarti con esercizi risolti passo dopo passo. Infine, vi mostriamo la dimostrazione della formula del derivato dell’arcocoseno.

Qual è la derivata dell’arcocoseno?

La derivata dell’arcocoseno di x è negativa di uno sulla radice quadrata di uno meno x al quadrato.

$f(x)=\text{arccos}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{1}{\sqrt{1-x^2}}$

Pertanto, la derivata dell’arcoseno di una funzione è uguale a meno il quoziente della derivata di quella funzione diviso per la radice quadrata di uno meno quella funzione al quadrato.

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

Infatti la prima formula si ottiene sostituendo u con x nella seconda formula. Quindi, per ricapitolare, la formula per la derivata del coseno inverso è:

Come puoi vedere, la formula per la derivata dell’arcoseno è come la derivata dell’arcoseno , ma aggiungendo prima un segno negativo.

Esempi di derivata dell’arcocoseno

Data la formula per la derivata della funzione arcocoseno, analizzeremo ora alcuni esempi di questo tipo di derivate trigonometriche. In questo modo ti sarà più semplice capire come si ricava l’arcocoseno di una funzione.

Esempio 1: Derivata dell’arcocoseno di 2x

$f(x)=\text{arccos}(2x)$

Per risolvere la derivata dell’arcocoseno usiamo la sua formula:

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

La derivata di 2x è 2, quindi la derivata dell’arcocoseno di 2x è negativa 2 sulla radice uno meno 2x al quadrato:

$f(x)=\text{arccos}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2}{\sqrt{1-(2x)^2}}=-\cfrac{2}{\sqrt{1-4x^2}}$

Esempio 2: Derivata dell’arcocoseno di x al quadrato

$f(x)=\text{arccos}(x^2)$

Applichiamo la formula della derivata dell’arcocoseno con la regola della catena per calcolare la derivata:

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

Poiché la derivata della funzione x ² è 2x, la derivata dell’arcocoseno di x elevato a 2 è:

$f(x)=\text{arccos}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{\sqrt{1-\left(x^2\right)^2}}=-\cfrac{2x}{\sqrt{1-x^4}}$

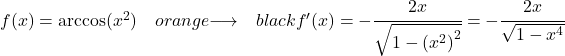
Esempio 3: Derivata dell’arcocoseno di un logaritmo

$f(x)=\text{arccos}\bigl(\ln (x)\bigr)$

La funzione in questo esempio è una funzione composta da un arcocoseno e un logaritmo naturale, quindi dobbiamo utilizzare la regola della catena per ricavarla.

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

La derivata del logaritmo naturale è una divisa per x, quindi la derivata della funzione intera è:

$f(x)=\text{arccos}\bigl(\ln (x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{\cfrac{1}{x}}{\sqrt{1-\left(\ln(x)\right)^2}}=\cfrac{1}{x\sqrt{1-\ln^2(x)}}$

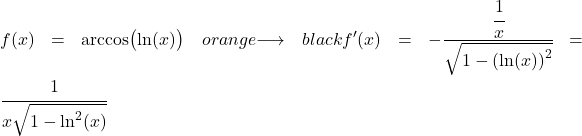
Problemi risolti del derivato dell’arcocoseno

Derivare le seguenti funzioni arcocoseno:

$\text{A) }f(x)=\text{arccos}(7x)$

$\text{B) }f(x)=\text{arccos}(x^3+6x)$

$\text{C) }f(x)=\text{arccos}^3\left(e^{3x}\right)$

$\text{D) }f(x)=\text{arccos}\left(\log_3(x^3)\right)$

$\text{E) }f(x)=\text{arccos}\left(\sqrt{4x}\right)$

vedi soluzione

$\text{A) }f'(x)=-\cfrac{7}{\sqrt{1-(7x)^2}}=-\cfrac{7}{\sqrt{1-49x^2}}$

$\text{B) }f'(x)=-\cfrac{3x^2+6}{\sqrt{1-(x^3+6x)^2}}$

$\begin{aligned}\text{C) }\displaystyle f'(x)&=3\text{arccos}^2\left(e^{3x}\right)\cdot \left(-\frac{3e^{3x}}{\sqrt{1-\left(e^{3x}\right)^2}}\right)\\[1.5ex] &=-\cfrac{9\text{arccos}^2\left(e^{3x}\right)\cdot e^{3x}}{\sqrt{1-e^{6x}}}\end{aligned}$

$\begin{aligned}\text{D) }f'(x)&=-\cfrac{1}{\sqrt{1-\left(\log_3(3x)\right)^2}}\cdot \cfrac{3}{3x\cdot \ln 3}\\[1.5ex] &=-\cfrac{1}{x\cdot \ln 3\cdot \sqrt{1-\log_3^2(3x)}} \end{aligned}$

$\begin{aligned}\text{E) } f'(x)& =-\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=-\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=-\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}$