In questo articolo spieghiamo come derivare l’arcosecante iperbolico di una funzione. Troverai anche esempi pratici della derivata dell’arcosecante iperbolico.
Formula per la derivata dell’arco cosecante iperbolico
La derivata dell’arco cosecante iperbolico di x è uguale a meno 1 diviso per il prodotto di x per la radice di uno più x al quadrato.
![]()
Pertanto, la derivata dell’arco cosecante iperbolico di una funzione è meno la derivata di detta funzione divisa per il prodotto della funzione per la radice di uno più la funzione quadrata.
![]()
In sintesi, la formula per calcolare la derivata della funzione arcosecante iperbolica è:
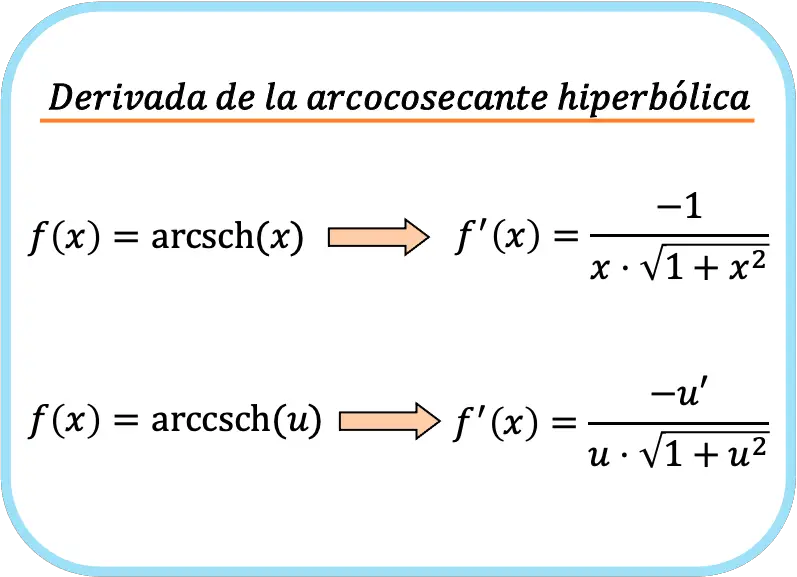
Anche se abbiamo messo due formule, ciò non significa che siano diverse. Se guardi da vicino, la seconda formula è come la prima ma applica la regola della catena.
Esempi di derivata dell’arco cosecante iperbolico
Data la formula per la derivata dell’arco cosecante iperbolico, deriveremo quindi due di queste funzioni in modo da poter vedere come si fa.
Esempio 1
![]()
In questo esercizio dobbiamo utilizzare la formula per la derivata dell’arco cosecante iperbolico con la regola della catena, perché nell’argomento è presente una funzione diversa da x:
![]()
Quindi, per trovare la derivata, dobbiamo sostituire la u con 3x e la u’ con la sua derivata, che è 3:
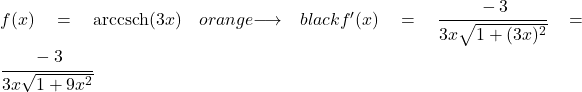
Esempio 2
![]()
In questo caso abbiamo una funzione polinomiale nell’argomento arcosecante iperbolico, quindi dobbiamo usare anche la regola della catena per derivarla:
![]()
Quindi inseriamo la derivata della funzione argomento al numeratore della frazione e al denominatore cambiamo la u con la funzione polinomiale:
![Rendered by QuickLaTeX.com \begin{aligned}f(x)=\text{arccsch}(x^5-2x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}f'(x)&=\cfrac{-(5x^4-6x^2)}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\\[1.5ex] &=\cfrac{-5x^4+6x^2}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6257584425bd348ba75c7680d8ff6f70_l3.png)