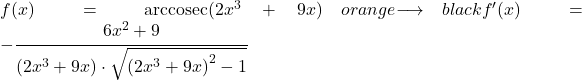In questa pagina vedrai qual è la formula per la derivata dell’arcosecante. Inoltre, potrai vedere esercizi risolti per le derivate dell’arco cosecante di una funzione.
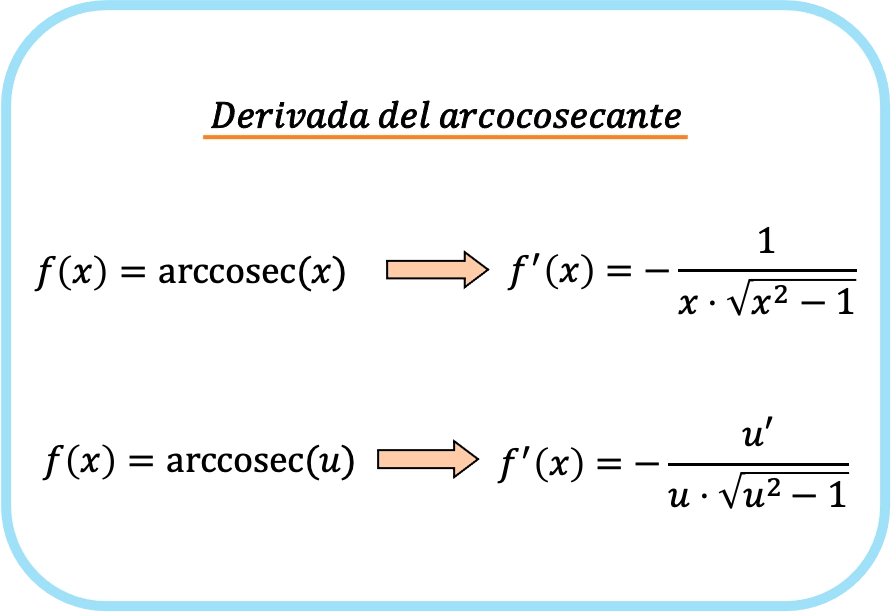
Formula del derivato arcosecante
La derivata dell’arcosecante di x è negativa uno sul prodotto di x per la radice di x al quadrato meno 1.
![]()
Pertanto, la derivata dell’arcosecante di una funzione è uguale a meno il quoziente della derivata di quella funzione diviso per la funzione moltiplicata per la radice di quella funzione al quadrato meno uno.
![]()
Infatti le due formule precedenti sono uguali, ma nella seconda espressione si applica la regola della catena. Infatti, se sostituisci la funzione identità x nella u, otterrai la derivata dell’arcosecante di x poiché la derivata di x è uno.
Come ben sai, l’arcosecante è la funzione trigonometrica inversa della cosecante, tuttavia le sue derivate sono abbastanza diverse. Puoi vedere la formula per quest’altro tipo di funzione trigonometrica nel seguente link:
➤ Vedi: derivata della cosecante
Esempi di derivata dell’arco cosecante
Vedendo cos’è la regola della derivata arcocosecante, risolveremo due esempi di questo tipo di derivata. Ma se hai ancora qualche domanda su come ricavare l’arco cosecante, puoi chiedercela nei commenti.
Esempio 1
In questo esempio vedremo quanto vale la derivata dell’arco cosecante della funzione quadratica x 2 .
![]()
Per calcolare la derivata dell’arcosecante di x al quadrato applichiamo la formula che abbiamo visto sopra:
![]()
La derivata di x elevata a due è 2x, quindi la derivata della funzione composta è:
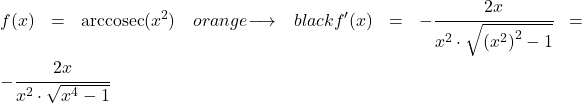
Esempio 2
In questo secondo esempio deriveremo l’arcosecante di una funzione potenziale.
![]()
Dobbiamo usare la regola della derivata dell’arcosecante per trovare la derivata dell’intera funzione.
![]()
Quindi, al numeratore scriviamo la derivata dell’argomento della funzione, e al denominatore riscriviamo la funzione potenziale e la moltiplichiamo per la radice quadrata della funzione dell’argomento al quadrato meno 1: