▷ Derivata di una sottrazione (formula ed esercizi risolti)

In questo articolo spieghiamo come derivare una sottrazione di funzioni (formula). Troverai anche esempi di derivate di sottrazione ed esercizi risolti passo passo per esercitarti.

Formula per la derivata di una sottrazione

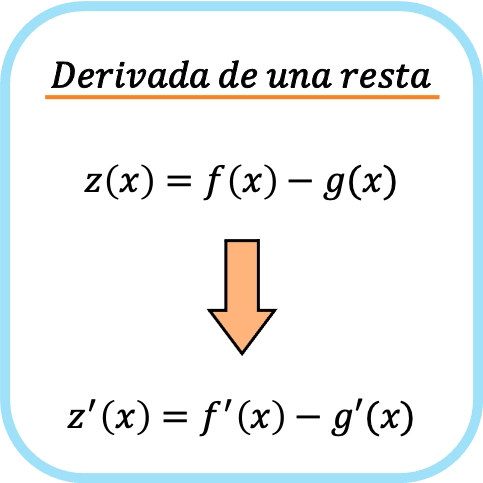
La derivata della sottrazione di due funzioni equivale a sottrarre la derivata di ciascuna funzione separatamente.

$z(x)=f(x)-g(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} z'(x)=f'(x)-g'(x)$

In altre parole, differenziare due funzioni separatamente e poi sottrarle equivale a prima sottrarre le funzioni e poi derivare.

Allo stesso modo, la stessa regola di differenziazione si applica alle sottrazioni di due o più funzioni, quindi se abbiamo una sottrazione di tre, quattro, cinque,… funzioni, dobbiamo differenziarle separatamente e poi sottrarle.

$\begin{array}{c}z(x)=f(x)- g(x)- h(x)- \dots\\[1.5ex]\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex]z'(x)=f'(x)-g'(x)- h'(x)- \dots\end{array}$

Come puoi vedere, la formula per la derivata di una differenza di funzioni è molto simile alla regola per la derivata di una somma.

➤ Vedi:derivata di una somma di funzioni

Esempi di derivata di sottrazione

Una volta vista qual è la formula per la derivata di una sottrazione, passiamo ora ad analizzare alcuni esempi di derivate di questo tipo di operazioni per comprendere appieno come si derivano le sottrazioni di funzioni.

Esempio 1: Derivata di una sottrazione di funzioni potenziali

$f(x)=x^3-4x$

La derivata della sottrazione di due funzioni equivale alla differenza delle derivate di ciascuna funzione separatamente. Calcoleremo quindi prima la derivata di ciascuna funzione separatamente:

$\cfrac{d}{dx} \ x^3=3x^2$

$\cfrac{d}{dx}\ 4x=4$

La derivata dell’intera funzione è quindi la seguente:

$f'(x)=3x^2-4$

Esempio 2: Derivata di una sottrazione di funzioni diverse

$f(x)=\text{cos}(x)-\log_7(x^2)$

Per differenziare le funzioni di sottrazione, devi prima differenziare le due funzioni separatamente e poi sottrarle.

$\cfrac{d}{dx} \ \text{cos}(x)=-\text{sen}(x)$

$\cfrac{d}{dx}\ \log_7 (x^2)=\cfrac{2x}{x^2\cdot \ln(7)}=\cfrac{2}{x\ln(7)}$

E dopo aver ricavato le due derivate, le sottraiamo con lo stesso ordine iniziale:

$f'(x)=-\text{sen}(x)-\cfrac{2}{x\ln(7)}$

Esempio 3: Derivata di una sottrazione al quadrato

$f(x)=\left(x^7-2x^3-9\right)^2$

In questo caso abbiamo una funzione composta, perché è una sottrazione tra tre funzioni al quadrato. Dobbiamo quindi utilizzare la formula per la derivata di una funzione potenziale e la regola della catena per calcolare la derivata dell’intera funzione:

$f(x)=2\left(x^7-2x^3-9\right)\cdot \left(7x^6-6x^2\right)$

➤ Vedi: formula per la derivata di una potenza

Esercizi risolti sulla derivata di una sottrazione

Derivare le seguenti sottrazioni di funzioni:

$\text{A) } f(x)=9x^3-5x$

$\text{B) } f(x)=4x^5-6x^4-x^2-4$

$\text{C) } f(x)=\left(-3x^7-2x^5\right)^4$

$\text{D) } f(x)=\ln(5x^2+3x)-\text{cos}(x)$

$\text{E) } f(x)=8x^3-e^{5x}-\sqrt{8x+2}$

Vedi la soluzione

$\text{A) } f'(x)=27x^2-5$

$\text{B) } f'(x)=20x^4-24x^3-2x$

$\text{C) } f'(x)=4\left(-3x^7-2x^5\right)^3\cdot (-21x^6-10x^4)$

$\text{D) } f'(x)=\cfrac{10x+3}{5x^2+3x}-\bilg(-\text{sen}(x)\bigr)=\cfrac{10x+3}{5x^2+3x}+\text{sen}(x)$

$\text{E) } f'(x)=24x^2-5e^{5x}-\cfrac{8}{2\sqrt{8x+2}}=24x^2-5e^{5x}-\cfrac{4}{\sqrt{8x+2}}$

Dimostrazione della derivata di una sottrazione

Successivamente, dimostreremo la formula per la derivata di una sottrazione di funzioni dalla definizione di derivata, che è:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Quindi se z è la differenza di due diverse funzioni:

$z(x)=f(x)-g(x)$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{z(x+h)-z(x)}{h}$

Sostituiamo z con la sottrazione delle funzioni nell’espressione limite:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{\bigl[f(x+h)-g(x+h)\bigr]-\bigl[f(x)-g(x)\bigr]}{h}$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)-g(x+h)-f(x)+g(x)}{h}$

Effettueremo ora una trasformazione per separare la frazione e ottenere una sottrazione di due frazioni:

$\displaystyle z'(x)=\lim_{h \to 0}\left[\frac{f(x+h)-f(x)}{h}+\frac{-g(x+h)+g(x)}{h}\right]$

$\displaystyle z'(x)=\lim_{h \to 0}\left[\frac{f(x+h)-f(x)}{h}-\frac{g(x+h)-g(x)}{h}\right]$

Applicando le leggi dei limiti, possiamo separare l’espressione di cui sopra in due limiti diversi. Poiché il limite di una sottrazione è uguale alla sottrazione dei limiti:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}-\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}$

Se guardi da vicino, ogni limite corrisponde alla derivata di una funzione, il che significa che la formula per la derivata di una differenza è soddisfatta:

$\displaystyle z'(x)=f'(x)-g'(x)$

Derivato di una sottrazione