Qui ti spieghiamo come derivare una potenza (o funzione potenziale), troverai la formula per la derivata di una potenza, diversi esempi e potrai anche esercitarti con esercizi risolti passo dopo passo.
Formula per la derivata di una potenza
La derivata di una potenza, o funzione potenziale, è il prodotto dell’esponente della potenza per la base elevata all’esponente meno 1 per la derivata della base.
![]()
Pertanto, se la base è la funzione identità , per ottenere la potenza è sufficiente moltiplicare la funzione per l’esponente e sottrarre all’esponente un’unità:
![]()
Infatti, la derivata della funzione identità è uguale a 1.
In sintesi, per ricavare una funzione potenziale esistono due formule: la prima che si può sempre usare e la seconda che si può applicare solo quando la base è una x.
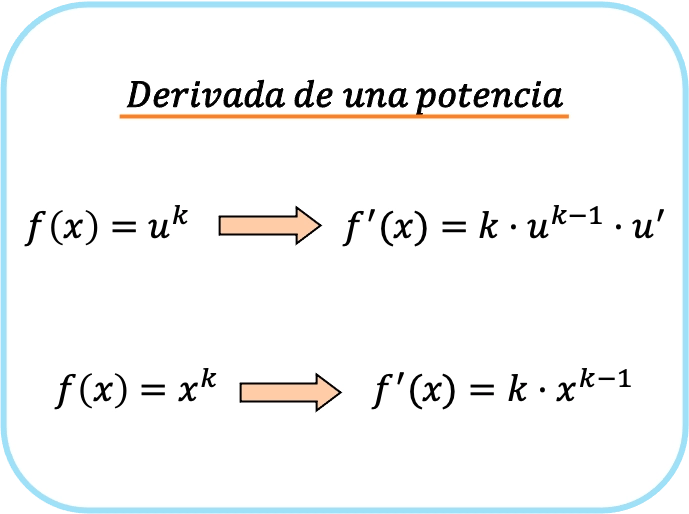
Possiamo facilmente verificare che la prima formula presentata per la derivata di una potenza è come la seconda ma applicando la regola della catena.
Nota che queste formule si possono usare solo quando la variabile è la base della potenza, se la x è al denominatore devi applicare la regola per la derivata di una funzione esponenziale:
➤ Vedi: derivata di una funzione esponenziale
Esempi di derivati della potenza
Dopo aver visto la formula per la derivata di una funzione potenziale, spiegheremo alcuni esempi di questo tipo di derivata in modo che tu possa capire come si derivano le potenze.
Esempio 1: Derivata di una potenza di base x
![]()
Come abbiamo spiegato nella sezione precedente, quando la base della potenza è solo una x, la formula che dobbiamo usare per derivare la funzione è:
![]()
La derivata della potenza x elevata a 4 è quindi:
![]()
Esempio 2: Derivata di una potenza con parentesi
![]()
In questo esempio la base non è la funzione identità, dobbiamo quindi utilizzare la formula generale per la derivata di una potenza:
![]()
La funzione tra parentesi è una funzione lineare, quindi la sua derivata è 2. Pertanto, la derivata dell’intera funzione potenziale è:
![]()
Esempio 3: Derivata di una potenza negativa
![]()
In questo caso abbiamo una funzione potenziale il cui esponente è negativo e la cui base è un logaritmo, quindi utilizzeremo la seguente formula per differenziare la funzione:
![]()
Anche se l’esponente della potenza è negativo, bisogna sottrarne anche uno. La derivata della funzione è quindi:
![]()
Se hai dubbi sulla soluzione, puoi consultare la formula per la derivata di una funzione logaritmica qui:
➤ Vedi: derivata di una funzione logaritmica
Esempio 4: Derivata di una potenza con radice
![]()
La funzione in questo esempio è una potenza all’interno di un’espressione regolare. Tuttavia, i radicali possono essere trasformati in espressioni potenziali, quindi la funzione può essere semplificata convertendola in una funzione potenziale con esponente frazionario:
![]()
Applichiamo ora la formula per la derivata di una potenza di una variabile:
![]()
E la derivata è:
![]()
Puoi anche distinguere tra questi tipi di funzioni utilizzando la regola della derivata radice:
➤ Vedi: derivato da una radice
Esercizi risolti sulla derivata di una potenza
Calcolare la derivata delle seguenti potenze:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
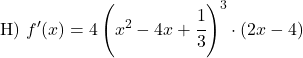
![]()