Derivata di un quoziente (divisione): formula ed esercizi svolti

In questo articolo spieghiamo come ricavare un quoziente (o divisione) da due funzioni. Troverai esempi di derivate di quozienti di funzioni e, inoltre, potrai esercitarti con esercizi passo passo sulle derivate di divisioni.

Formula per la derivata di un quoziente

La derivata di un coefficiente (o divisione) delle funzioni è identica alla derivata della funzione numeratore per la funzione denominatore minore della funzione numeratore per la derivata della funzione denominatore divisa per il quadrato della funzione denominatore alto.

formula per la derivata di una divisione o quoziente

Come puoi vedere, quando applichiamo la regola per la derivata di un quoziente (o di una divisione) abbiamo ancora una frazione dopo la differenziazione. Ma, in più, al numeratore abbiamo due moltiplicazioni e una sottrazione, e il denominatore è elevato alla potenza di due.

Esempi di derivate di quozienti

Abbiamo appena visto qual è la formula per la derivata di un quoziente di due funzioni, risolveremo poi alcuni esempi di derivate di questo tipo di operazioni. Ricorda, se non capisci come si ricava un quoziente funzionale, puoi chiedercelo nella sezione commenti.

Esempio 1

In questo esempio, deriveremo una funzione potenziale divisa per una funzione trigonometrica:

$f(x)=\cfrac{3x^2+4x}{\text{sen}(2x)}$

La formula per la derivata di una divisione di due funzioni diverse è la seguente:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

Quindi dobbiamo prima calcolare separatamente la derivata di ciascuna funzione:

$\cfrac{d}{dx}\ (3x^2+4x)=6x+4$

$\cfrac{d}{dx}\ \text{sen}(2x)=2\text{cos}(2x)$

La derivata dell’intera funzione è quindi:

$\begin{array}{c}f(x)=\cfrac{3x^2+4x}{\text{sen}(2x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(6x+4)\cdot\text{sen}(2x)-(3x^2+4x)\cdot 2\text{cos}(2x)}{\text{sen}^2(2x)}\end{array}$

Esempio 2

In questo caso troveremo la derivata di una costante divisa per una funzione:

$f(x)=\cfrac{10}{x^2+3x-9}$

Come abbiamo visto sopra, la regola per la derivata di una divisione di due funzioni diverse è la seguente:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

Quindi, calcoliamo separatamente la derivata del numeratore e del denominatore:

$\cfrac{d}{dx}\ 10=0$

$\cfrac{d}{dx}\ (x^2+3x-9)=2x+3$

Infine troviamo la derivata della divisione intera:

$\begin{array}{c}f(x)=\cfrac{10}{x^2+3x-9}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{0\cdot (x^2+3x-9)-10\cdot (2x+3)}{\left(x^2+3x-9\right)^2}=\cfrac{-20x+30}{\left(x^2+3x-9\right)^2}\end{array}$

Infatti, possiamo ricavare una formula per differenziare direttamente quando abbiamo una costante al numeratore divisa per una funzione, perché la derivata della costante è sempre 0. Pertanto, la seguente formula sarà sempre vera:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=\cfrac{k}{f(x)} \\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{-k\cdot f'(x)}{\bigl(f(x)\bigr)^2}\end{array} \end{empheq}$

Esempio 3

In questo esercizio deriveremo il quoziente di due polinomi:

$f(x)=\cfrac{x^3+4x^2}{5x^2-8}$

Per risolvere la derivata dobbiamo applicare la regola della derivata di un quoziente di due funzioni diverse, che è la seguente:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

Ora troviamo la derivata del polinomio al numeratore e del polinomio al denominatore:

$\cfrac{d}{dx}\ (x^3+4x^2)=3x^2+8x$

$\cfrac{d}{dx}\ (5x^2-8)=10x$

La derivata della divisione dei polinonimi è quindi:

$\begin{array}{c}f(x)=\cfrac{x^3+4x^2}{5x^2-8}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\end{array}$

E infine, eseguiamo le operazioni e semplifichiamo il più possibile la frazione:

$\begin{aligned}f'(x)&=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\\[2ex]&=\cfrac{15x^4-24x^2+40x^3-64x-10x^4-40x^3}{25x^4+64-80x^2}\\[2ex]&=\cfrac{5x^4-24x^2-64x}{25x^4-80x^2+64}\end{aligned}$

Esercizi risolti sulla derivata di un quoziente

Derivare le seguenti divisioni di funzioni:

$\text{A) }f(x)=\cfrac{9x^2+5x}{6x^3}$

$\text{B) }f(x)=\cfrac{19}{2x^2-2}$

$\text{C) }f(x)=\cfrac{8x^3-4x^2+3x}{e^{4x}}$

$\text{D) }f(x)=\cfrac{\text{cos}(x^2)}{\text{sen}(6x)}$

$\text{E) }f(x)=\cfrac{\ln(x^3+4)}{\left(4x^2-3x\right)^3}$

$\text{F) }f(x)=\cfrac{\sqrt{x^2+4x}}{5^{x^2}}$

Vedi la soluzione

$\begin{aligned}\text{A) }f'(x)&=\cfrac{(18x+5)\cdot 6x^3-(9x^2+5x)\cdot 18x^2}{\left(6x^3\right)^2}\\[1.5ex]&=\cfrac{108x^4+30x^3-162x^4-90x^3}{36x^6}\\[1.5ex]&=\cfrac{-54x^4-60x^3}{36x^6}\\[1.5ex]&=\cfrac{-9x-10}{6x^3}\end{aligned}$

$\text{B) }f'(x)=\cfrac{-19\cdot 4x}{\left(2x^2-2\right)^2}=\cfrac{-76x}{\left(2x^2-2\right)^2}$

$\begin{aligned}\text{C) }f'(x)&=\cfrac{(24x^2-8x+3)e^{4x}-(8x^3-4x^2+3x)\cdot 4e^{4x}}{\left(e^{4x}\right)^2}\\[1.5ex]&=\cfrac{e^{4x}(24x^2-8x+3-32x^3+16x^2-12x)}{e^{8x}}\\[1.5ex]&=\cfrac{-32x^3+40x^2-20x+3}{e^{4x}}\end{aligned}$

$\text{D) }f'(x)=\cfrac{-2x\text{sen}(x^2)\cdot\text{sen}(6x)-\text{cos}(x^2)\text{cos}(6x)\cdot 6}{\text{sen}^2(6x)}$

$\begin{aligned}\text{E) }f'(x)&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(\left(4x^2-3x\right)^3\right)^2}\\[1.5ex]&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(4x^2-3x\right)^6}\end{aligned}$

$\begin{aligned}\text{F) }f'(x)&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{\left(5^{x^2}\right)^2}\\[1.5ex]&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{5^{2x^2}}\end{aligned}$

Dimostrazione della derivata di un quoziente

Infine, dimostreremo la formula per la derivata di una divisione. Per fare ciò, utilizzeremo la definizione generale di derivata, che è:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Sia z la divisione di due diverse funzioni:

$z(x)=\cfrac{f(x)}{g(x)}$

Quindi, la derivata della funzione z applicando la definizione matematica sarà:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\cfrac{f(x+h)}{g(x+h)}-\cfrac{f(x)}{g(x)}}{h}$

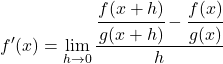
Risolviamo la sottrazione delle frazioni dal numeratore della frazione:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\cfrac{f(x+h)\cdot g(x)}{g(x+h)\cdot g(x)}-\cfrac{f(x)\cdot g(x+h)}{g(x)\cdot g(x+h)}}{h}$

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x)-f(x)\cdot g(x+h)}{h\cdot g(x)\cdot g(x+h)}$

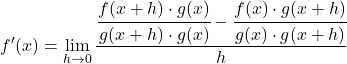
L’aggiunta di un termine di addizione e sottrazione a un’equazione non modifica l’equazione. Possiamo quindi passare allo step successivo:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x)\color{orange}\bm{-f(x)\cdot g(x)}\color{black}-f(x)\cdot g(x+h)\color{orange}\bm{+f(x)\cdot g(x)}\color{black}}{h\cdot g(x)\cdot g(x+h)}$

Estraiamo il fattore comune:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{g(x)\bigl[f(x+h)-f(x)\bigr]-f(x)\bigl[g(x+h)-g(x)\bigr]}{h\cdot g(x)\cdot g(x+h)}$

Ora spostiamo il termine h dal denominatore al numeratore utilizzando le proprietà delle frazioni:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{g(x)\cdot \cfrac{f(x+h)-f(x)\cdot g(x)}{h}-f(x)\cdot\cfrac{g(x+h)-g(x)}{h}}{g(x)\cdot g(x+h)}$

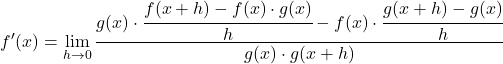
Trasformiamo l’equazione applicando le proprietà dei limiti:

$\displaystyle f'(x)=\frac{g(x)\cdot \displaystyle\lim_{h \to 0}\cfrac{f(x+h)-f(x)\cdot g(x)}{h}-f(x)\cdot\lim_{h \to 0}\cfrac{g(x+h)-g(x)}{h}}{g(x)\cdot \displaystyle\lim_{h \to 0}g(x+h)}$

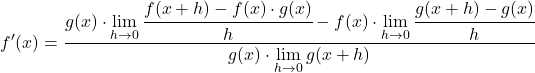
I limiti del numeratore corrispondono proprio alla definizione matematica della derivata di ciascuna funzione, quindi:

$\displaystyle f'(x)=\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{g(x)\cdot \displaystyle\lim_{h \to 0}g(x+h)}$

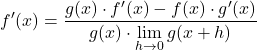
Risolviamo il limite del denominatore della frazione:

$\displaystyle f'(x)=\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{g(x)\cdot g(x)}$

E così si dimostra la formula per la derivata di un quoziente di due funzioni:

$\displaystyle f'(x)=\frac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}$

Derivata di un quoziente (o divisione)

Formula per la derivata di un quoziente

Esempi di derivate di quozienti

Esempio 1

Esempio 2

Esempio 3

Esercizi risolti sulla derivata di un quoziente

Dimostrazione della derivata di un quoziente

Lascia un commento Annulla risposta