▷ Derivata di un prodotto (formula ed esercizi risolti)

In questo articolo spieghiamo come derivare il prodotto di due funzioni (formula). Inoltre, potrai vedere diversi esempi di derivate di prodotti di funzioni e anche esercitarti con esercizi risolti sulle derivate di moltiplicazione.

Formula per la derivata di un prodotto

La derivata di un prodotto di due funzioni diverse è uguale al prodotto della derivata della prima funzione per la seconda funzione indifferenziata più il prodotto della prima funzione indifferenziata per la derivata della seconda funzione.

In altre parole, se f(x) e g(x) sono due funzioni diverse, la formula per la derivata della moltiplicazione tra le due funzioni è la seguente:

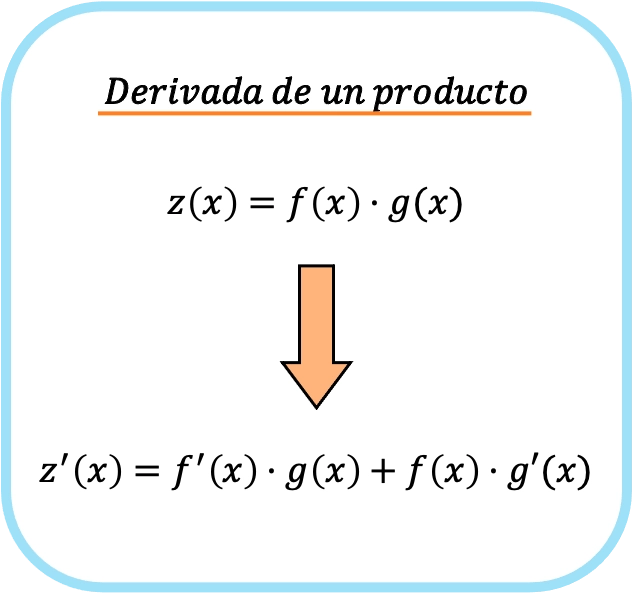
Quindi, applicando la regola della derivata di un prodotto, si passa da una semplice moltiplicazione a due prodotti diversi.

Esempi di derivato di un prodotto

Una volta che sappiamo qual è la formula per la derivata di un prodotto (o moltiplicazione), risolveremo diversi esempi di questo tipo di derivata. Ciò renderà molto più semplice capire come viene derivato il prodotto di due funzioni.

Esempio 1

In questo esempio risolveremo la derivata di due funzioni potenziali moltiplicando:

$f(x)=5x^2\cdot (x^3+4x-6)$

Come abbiamo visto nella sezione precedente, la formula per la derivata della moltiplicazione è:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

Pertanto, dobbiamo prima calcolare separatamente la derivata di ciascuna funzione:

$\cfrac{d}{dx}\ 5x^2=10x$

$\cfrac{d}{dx}\ (x^3+4x-6)=3x^2+4$

E una volta conosciuta la derivata di ciascuna funzione, possiamo applicare la formula per la derivata del prodotto di due funzioni. Cioè moltiplichiamo la derivata del primo fattore per il secondo fattore senza differenziare, quindi aggiungiamo il prodotto del primo fattore senza differenziare per la derivata del secondo fattore:

$\begin{array}{c}f(x)=5x^2\cdot (x^3+4x-6)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\end{array}$

Infine effettuiamo le operazioni per semplificare il risultato ottenuto:

$\begin{aligned}f'(x)& =10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\\[1.5ex] & = 10x^4+40x^2-60x +15x^4+20x^2 \\[1.5ex] & = 25x^4+60x^2-60x\end{aligned}$

Esempio 2

In questo caso deriveremo il prodotto di una costante da una funzione:

$f(x)=7\cdot (x^2+3x)$

La regola derivativa di un prodotto è la seguente:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

Pertanto, ricaviamo separatamente ciascuna funzione che fa parte del prodotto:

$\cfrac{d}{dx}\ 7=0$

$\cfrac{d}{dx}\ (x^2+3x)=2x+3$

E poi applichiamo la regola per la derivata di una moltiplicazione:

$\begin{array}{c}f(x)=7\cdot (x^2+3x)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=0\cdot (x^2+3x)+7\cdot (2x+3)=14x+21\end{array}$

Nota che la derivata di una costante è sempre zero, quindi possiamo dedurre che la derivata della moltiplicazione di una costante per una funzione è uguale al prodotto della costante e della derivata della funzione.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=k\cdot f(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=k\cdot f'(x)\end{array} \end{empheq}$

Esempio 3

Risolviamo il prodotto tra una funzione esponenziale e un logaritmo naturale:

$f(x)=4^{3x}\cdot \ln(x^2)$

La formula per la derivata di una moltiplicazione di due funzioni è:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

Dobbiamo quindi prima fare separatamente le derivate di ciascuna funzione che forma il prodotto, che sono le seguenti:

$\cfrac{d}{dx}\ 4^{3x}=4^{3x}\cdot \ln (4) \cdot 3$

$\cfrac{d}{dx}\ \ln(x^2)=\cfrac{2x}{x^2}=\cfrac{2}{x}$

Il prodotto derivato delle funzioni è quindi:

$\begin{array}{c}f(x)=4^{3x}\cdot \ln(x^2)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=4^{3x}\cdot \ln (4) \cdot 3\cdot \ln(x^2) +4^{3x}\cdot \cfrac{2}{x} \end{array}$

Esercizi risolti sulla derivata di un prodotto

Deriva i seguenti prodotti di funzione:

$\text{A) }f(x)=5\ln(3x)$

$\text{B) }f(x)=(4x^2+1)(6x^3-7)$

$\text{C) }f(x)=\text{cos}(4x)\cdot e^{x^2}$

$\text{D) }f(x)=(3x^3-4x^2+8x)\cdot \sqrt{6x^2+3x}$

$\text{E) }f(x)=5^{4x}\cdot \log_9(x^3-x)$

$\text{F) }f(x)=\left(10x^6-6x^5\right)^4\cdot \text{arcsen}(x^2+9x)$

Vedi la soluzione

$\text{A) } f'(x)=5\cdot \cfrac{3}{3x} =\cfrac{5}{x}$

$\begin{aligned}\text{B) }f'(x)&=8x\cdot (6x^3-7)+(4x^2+1)\cdot 18x^2\\[1.2ex]&=48x^4-56x+72x^4+18x^2\\[1.2ex]&=120x^4+18x^2-56x \end{aligned}$

$\text{C) }f'(x) =-4\text{sen}(4x)\cdot e^{x^2}+\text{cos}(4x)\cdot e^{x^2}\cdot 2x$

$\text{D) }f'(x)=(9x^2-8x+8)\cdot \sqrt{6x^2+3x}+(3x^3-4x^2+8x)\cdot\cfrac{12x+3}{2\sqrt{6x^2+3x}}$

$\text{E) }f'(x)=5^{4x}\cdot \ln(5) \cdot 4 \cdot \log_9(x^3-x)+ 5^{4x}\cdot\cfrac{3x^2-1}{(x^3-x)\ln(9)}$

$\begin{aligned}\text{F) }f'(x)=& 4\left(10x^6-6x^5\right)^3\cdot (60x^5-30x^4)\cdot \text{arcsen}(x^2+9x)\ +\\[1.2ex] &+\left(10x^6-6x^5\right)^4\cdot \cfrac{2x+9}{\sqrt{1-\left(x^2+9x\right)^2}}\end{aligned}$

Derivato da un prodotto a tre funzioni

Successivamente, ti lasciamo con la formula per la derivata della moltiplicazione di 3 funzioni, poiché è molto simile a quella di 2 funzioni e può essere utile in alcuni casi.

La derivata del prodotto di tre funzioni è uguale al prodotto della derivata della prima funzione e delle altre due funzioni, più il prodotto della derivata della seconda funzione e delle altre due funzioni, più il prodotto della derivata delle terza funzione.funzione dalle altre due funzioni.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=1mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=f(x)\cdot g(x)\cdot h(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)\cdot h(x)+f(x)\cdot g'(x)\cdot h(x)+f(x)\cdot g(x)\cdot h'(x)\end{array} \end{empheq}$

Ad esempio, se vogliamo derivare la seguente moltiplicazione di tre diverse funzioni:

$f(x)=3x\cdot e^{2x} \cdot \text{sen}(x)$

Per risolvere la derivata dobbiamo applicare la regola della derivata del prodotto di tre funzioni, quindi:

$f'(x)=3\cdot e^{2x} \cdot \text{sen}(x)+3x\cdot 2e^{2x} \cdot \text{sen}(x)+3x\cdot e^{2x} \cdot \text{cos}(x)$

Dimostrazione della formula per la derivata di un prodotto

Infine, dimostreremo la formula per la derivata di una moltiplicazione. Non è necessario memorizzarlo, ma è sempre bene capire da dove provengono le formule. 🙂

Dalla definizione matematica della derivata:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Sia la funzione z il prodotto di due diverse funzioni:

$z(x)=f(x)\cdot g(x)$

Allora la derivata di z , secondo la definizione, sarà:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{\bigl[f(x+h)\cdot g(x+h)\bigr]-\bigl[f(x)\cdot g(x)\bigr]}{h}$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)-f(x)\cdot g(x)}{h}$

Come sappiamo, se aggiungiamo un termine sommando e sottraendo, ciò non influisce sul risultato purché entrambi siano lo stesso termine. Possiamo quindi passare allo step successivo:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)\color{orange}\bm{-f(x+h)\cdot g(x)+f(x+h)\cdot g(x)}\color{black}-f(x)\cdot g(x)}{h}$

Ora utilizziamo le proprietà del confine per separare il confine precedente in due confini diversi:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)-f(x+h)\cdot g(x)}{h}+\lim_{h \to 0}\frac{f(x+h)\cdot g(x)-f(x)\cdot g(x)}{h}$

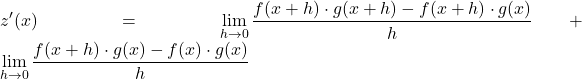
Estraiamo il fattore comune al numeratore delle due frazioni:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\bigl(g(x+h)-g(x)\bigr)}{h}+\lim_{h \to 0}\frac{g(x)\bigl(f(x+h)-f(x)\bigr)}{h}$

Conosciamo invece il risultato del seguente limite:

$\displaystyle \lim_{h \to 0}f(x+h)=f(x)$

Possiamo quindi semplificare i limiti:

$\displaystyle z'(x)=\lim_{h \to 0}f(x+h)\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}+\lim_{h \to 0}g(x)\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

$\displaystyle z'(x)=f(x)\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}+g(x)\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Infine, considerando i due limiti rimanenti, ciascuno corrisponde alla definizione di derivata di una funzione. L’uguaglianza può quindi essere semplificata:

$\displaystyle z'(x)=f(x)\cdot g'(x)+g(x)\cdot f'(x)$

O equivalente:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x) \end{empheq}$

Derivata di un prodotto (o moltiplicazione)

Formula per la derivata di un prodotto

Esempi di derivato di un prodotto

Esempio 1

Esempio 2

Esempio 3

Esercizi risolti sulla derivata di un prodotto

Derivato da un prodotto a tre funzioni

Dimostrazione della formula per la derivata di un prodotto

Lascia un commento Annulla risposta