Derivato dell'arcotangente iperbolico

Qui troverai come ricavare l’arcotangente iperbolico di una funzione. Potrai anche vedere esempi risolti di questo tipo di derivate trigonometriche e, infine, ti mostreremo la formula per la derivata dell’arcotangente iperbolico.

Formula per la derivata dell’arcotangente iperbolico

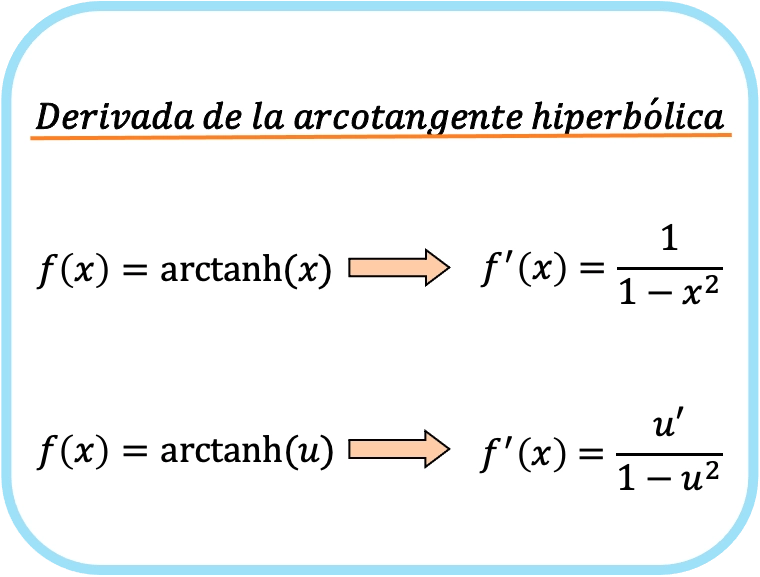
La derivata dell’arcotangente iperbolico di x è uno su uno meno x al quadrato.

$f(x)=\text{arctanh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{1-x^2}$

Pertanto, la derivata dell’arcotangente iperbolico di una funzione è uguale al quoziente della derivata di quella funzione diviso per uno meno detta funzione al quadrato.

$f(x)=\text{arctanh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}$

In realtà entrambe le formule sono uguali, ma nella seconda si applica la regola della catena. Ad esempio, sostituendo x con u otteniamo esattamente la prima formula poiché la derivata di x è 1.

Proprio come l’arcotangente è la funzione inversa della tangente, l’arcotangente iperbolico è l’inverso della tangente iperbolica. Anche così, le loro derivate sono molto diverse, puoi controllare la derivata di questa funzione trigonometrica qui:

➤ Vedi: formula per la derivata della tangente iperbolica

Esempi di derivata dell’arcotangente iperbolico

Esempio 1

$f(x)=\text{arctanh}(2x)$

Logicamente dobbiamo applicare la regola della derivata dell’arcotangente iperbolico:

$f(x)=\text{arctanh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}$

La derivata di 2x è 2, quindi metti due al numeratore della frazione e uno meno 2x al quadrato al denominatore:

$f(x)=\text{arctanh}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{1-(2x)^2}}=\cfrac{2}{1- 4x^2}$

Esempio 2

$f(x)=\text{arctanh}(e^{3x})$

Per risolvere la derivata di questa funzione, dobbiamo utilizzare la formula per la derivata dell’arcotangente iperbolico.

$f(x)=\text{arctanh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}$

Inoltre, la funzione argomento arcotangente iperbolico è una funzione composta, quindi dovremo applicare anche la regola della catena:

$f(x)=\text{arctanh}(e^{3x}) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3\cdot e^{3x}}{1-\left(e^{3x}\right)^2}=\cfrac{3e^{3x}}{1-3^{6x}}$

Dimostrazione della derivata dell’arcotangente iperbolico

In questa sezione finale, dimostreremo la formula per la derivata dell’arcotangente iperbolico.

$y=\text{arctanh}(x)$

Poiché l’arcotangente iperbolica è l’inversa della tangente iperbolica, possiamo esprimere l’uguaglianza precedente in un altro modo:

$x=\text{tanh}(y)$

Ora differenziamo entrambi i lati dell’equazione:

$1=\cfrac{1}{\text{cosh}^2(y)}\cdot y'$

Ti chiariamo:

$y'=\text{cosh}^2(y)$

Sappiamo invece che la differenza dei quadrati del coseno iperbolico e del seno iperbolico dà 1. Possiamo quindi trasformare l’espressione precedente in una frazione:

$\text{cosh}^2(y)-\text{senh}^2(y)=1$

$y'=\cfrac{\text{cosh}^2(y)}{1}=\cfrac{\text{cosh}^2(y)}{\text{cosh}^2(y)-\text{senh}^2(y)}$

Dividiamo tutti i termini della frazione per il quadrato del coseno iperbolico:

$y'=\cfrac{\cfrac{\text{cosh}^2(y)}{\text{cosh}^2(y)}}{\cfrac{\text{cosh}^2(y)}{\text{cosh}^2(y)}-\cfrac{\text{senh}^2(y)}{\text{cosh}^2(y)}}$

$y'=\cfrac{1}{1-\cfrac{\text{senh}^2(y)}{\text{cosh}^2(y)}}$

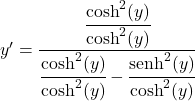
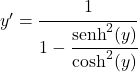
Il quoziente del seno iperbolico tra il coseno iperbolico è uguale alla tangente iperbolica, quindi:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

$y'=\cfrac{1}{1-\text{tanh}^2(y)}$

Ma, come abbiamo visto all’inizio della dimostrazione, la tangente iperbolica equivale alla variabile x, possiamo quindi sostituire l’espressione ottenendo così la formula per la derivata dell’arcotangente iperbolico:

$y'=\cfrac{1}{1-x^2}$

Derivata dell'arcotangente iperbolico

Formula per la derivata dell’arcotangente iperbolico

Esempi di derivata dell’arcotangente iperbolico

Esempio 1

Esempio 2

Dimostrazione della derivata dell’arcotangente iperbolico

Articoli simili

Lascia un commento Annulla risposta