In questo articolo imparerai come ricavare l’arcotangente di una funzione. Inoltre, potrai vedere esempi di questo tipo di derivata e anche esercitarti con esercizi risolti sulla derivata dell’arcotangente. Infine vi mostriamo anche la dimostrazione della formula per la derivata dell’arcotangente.
Qual è la derivata dell’arcotangente?
La derivata dell’arcotangente di x è uno su uno più x al quadrato.
![]()
Pertanto, la derivata dell’arcotangente di una funzione è uguale al quoziente della derivata di quella funzione diviso per uno più detta funzione al quadrato.
![]()
In questo caso la funzione era rappresentata da au, quindi questa sarebbe la formula per la derivata dell’arcotangente della funzione u.
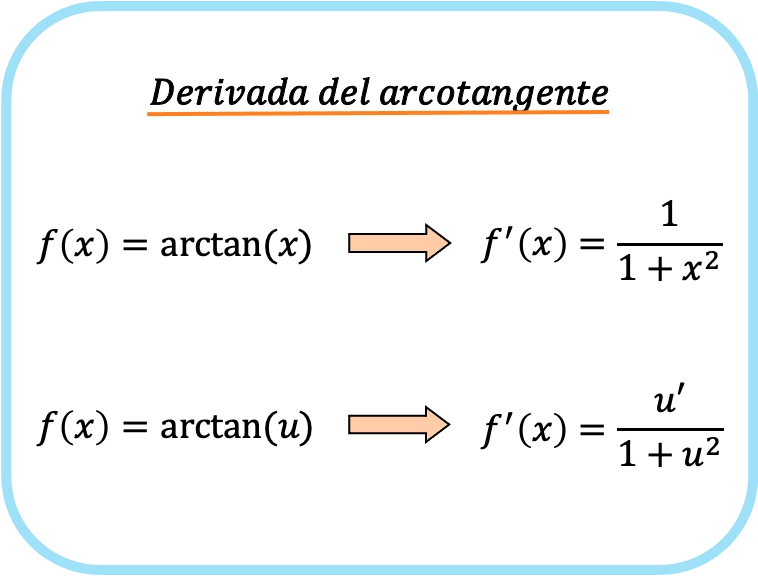
Come puoi vedere, la formula per la derivata dell’arcotangente è molto simile alle formule per le derivate dell’arcoseno e dell’arcocoseno.
Esempi di derivata dell’arcotangente
Una volta conosciuta la formula per la derivata dell’arcotangente, spiegheremo la derivazione di diversi esempi di questo tipo di derivate trigonometriche. In questo modo ti sarà più facile capire come viene derivato l’arcotangente di una funzione.
Esempio 1: Derivata dell’arcotangente di 2x
![]()
Applichiamo la formula per risolvere la derivata:
![]()
La derivata di 2x è 2, quindi la derivata arcotangente di 2x è 2 su uno più 2x al quadrato:
![]()
Esempio 2: Derivata dell’arcotangente di x al quadrato
![]()
Per trovare il risultato della derivata di questo esempio, dobbiamo utilizzare la formula per la derivata dell’arcotangente, che è:
![]()
Pertanto, la derivata della funzione x 2 è 2x, quindi la derivata dell’arcotangente di x elevata alla potenza di 2 è:
![]()
Esempio 3: Derivata dell’arcotangente del seno di x
![]()
Logicamente, per calcolare la derivata è necessario applicare la formula corrispondente:
![]()
In questo caso abbiamo una funzione composta, quindi dobbiamo applicare la regola della catena per calcolare la derivata dell’arcotangente:
![]()
Esercizi risolti sulla derivata dell’arcotangente
Derivare le seguenti funzioni arcotangente:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
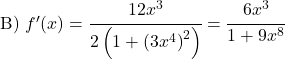
![]()
![]()
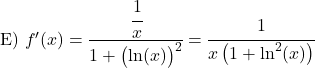
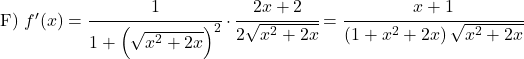
Dimostrazione della formula per la derivata dell’arcotangente
Successivamente dimostreremo la formula per la derivata dell’arcotangente.
![]()
Per prima cosa convertiamo l’arcotangente in tangente sfruttando il fatto che l’arcotangente è la funzione inversa della tangente:
![]()
Distinguiamo i due lati dell’equazione:
![]()
Cancelliamo e’:
![]()
D’altra parte, grazie all’identità trigonometrica fondamentale sappiamo che la somma dei quadrati del seno e del coseno è uguale a 1. Possiamo quindi trasformare l’espressione precedente in una frazione:
![]()
![]()
Dividiamo tutti i termini per il quadrato del coseno:
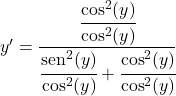
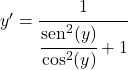
Il seno diviso per il coseno è uguale alla tangente, quindi:
![]()
![]()
Come abbiamo visto sopra la tangente equivale alla variabile x, possiamo quindi sostituire l’espressione per arrivare alla formula della derivata dell’arcotangente:
![]()