Derivato dell'arcosecante iperbolico

Qui troverai come calcolare la derivata dell’arcosecante iperbolico di una funzione. Inoltre, potrai vedere esempi risolti della derivata dell’arcosecante iperbolico.

Formula della derivata arcosecante iperbolica

La derivata dell’arcosecante iperbolico di x è uguale a meno 1 diviso per il prodotto di x per la radice di uno meno x al quadrato.

$f(x)=\text{arcsech}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-1}{x\sqrt{1-x^2}}$

Pertanto, la derivata dell’arcosecante iperbolico di una funzione è meno la derivata di quella funzione divisa per il prodotto della funzione per la radice di uno meno la funzione quadrata.

$f(x)=\text{arcsech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-u'}{u\sqrt{1-u^2}}$

In breve, la formula per la derivata della funzione arcosecante iperbolica è:

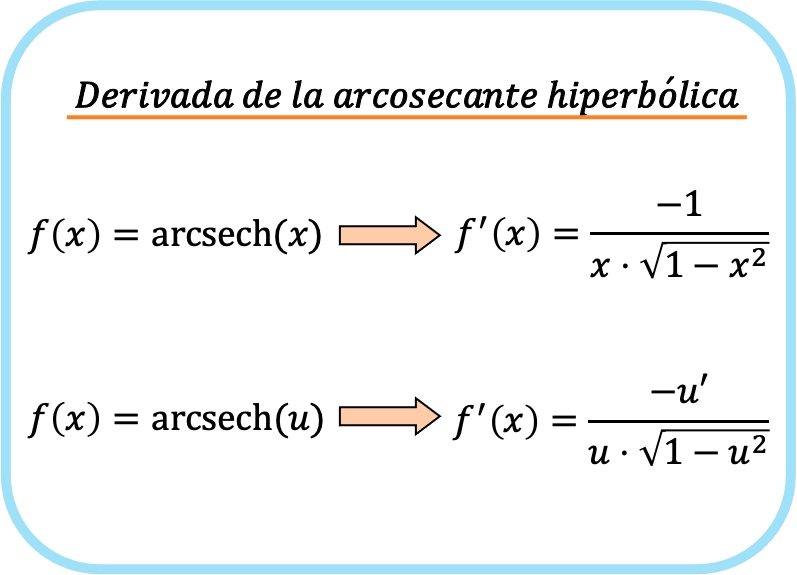
Entrambe le espressioni corrispondono in realtà alla stessa formula, ma alla seconda formula viene applicata la regola della catena. Infatti, se sostituisci u con la funzione identità x, otterrai la prima formula poiché la derivata di x è 1.

Esempi di derivata dell’arcosecante iperbolico

Dopo aver visto qual è la formula per la derivata dell’arcosecante iperbolico, risolveremo due esercizi passo passo di questo tipo di derivate trigonometriche inverse. Quindi puoi vedere esattamente come derivare l’arcosecante iperbolico di una funzione.

Esempio 1

In questo esempio, determineremo qual è la derivata dell’arcosecante iperbolico 2x.

$f(x)=\text{arcsech}(2x)$

Nell’argomento arcosecante iperbolico, abbiamo una funzione diversa da x, quindi dobbiamo utilizzare la formula della regola della catena per derivarla:

$f(x)=\text{arcsech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-u'}{u\sqrt{1-u^2}}$

La funzione 2x è lineare, quindi la sua derivata è 2. Pertanto, per trovare la derivata, sostituiamo semplicemente 2x con u e 2 con u’ nella formula:

$f(x)=\text{arcsech}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-2}{2x\sqrt{1-(2x)^2}}=\cfrac{-2}{2x\sqrt{1-4x^2}}$

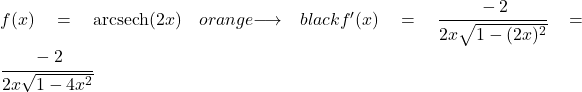
Esempio 2

In questo secondo esercizio deriveremo l’arcosecante iperbolico di una funzione polinomiale:

$f(x)=\text{arcsech}(x^3-4x)$

La funzione di questo esercizio è composta, perché l’arcosecante iperbolico ha un’altra funzione nel suo argomento. Quindi dobbiamo usare la formula della derivata arcosecante iperbolica con la regola della catena per fare la sua derivazione:

$f(x)=\text{arcsech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-u'}{u\sqrt{1-u^2}}$

Pertanto, al numeratore della frazione mettiamo la derivata della funzione polinomiale dell’argomento, e al denominatore cambiamo la u con la funzione polinomiale:

$\begin{aligned}f(x)=\text{arcsech}(x^3-4x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}f'(x)&=\cfrac{-(3x^2-4)}{(x^3-4x)\sqrt{1-(x^3-4x)^2}}\\[1.5ex] &=\cfrac{-3x^2+4}{(x^3-4x)\sqrt{1-(x^3-4x)^2}}\end{aligned}$

Derivata dell'arcosecante iperbolico

Formula della derivata arcosecante iperbolica

Esempi di derivata dell’arcosecante iperbolico

Esempio 1

Esempio 2

Articoli simili

Lascia un commento Annulla risposta