▷ Derivata della tangente (formula ed esercizi risolti)

Qui scoprirai come viene derivata la funzione tangente. Inoltre, potrai vedere esempi di derivata della tangente e anche esercitarti con esercizi risolti passo dopo passo. Infine, dimostriamo anche la formula della derivata tangente e ti mostriamo la formula della derivata tangente inversa.

Qual è la derivata della tangente?

La derivata della tangente di x è uguale a 1 sul quadrato del coseno di x. Anche la derivata della tangente di x è equivalente al quadrato della secante di x e 1 più il quadrato della tangente di x.

$\begin{array}{c}f(x)=\text{tan}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cos}^2(x)}=\text{sec}^2(x)=1+\text{tan}^2(x)\end{array}$

Tutte le espressioni sono equivalenti, quindi la funzione tangente ha tre possibili formule per derivarla.

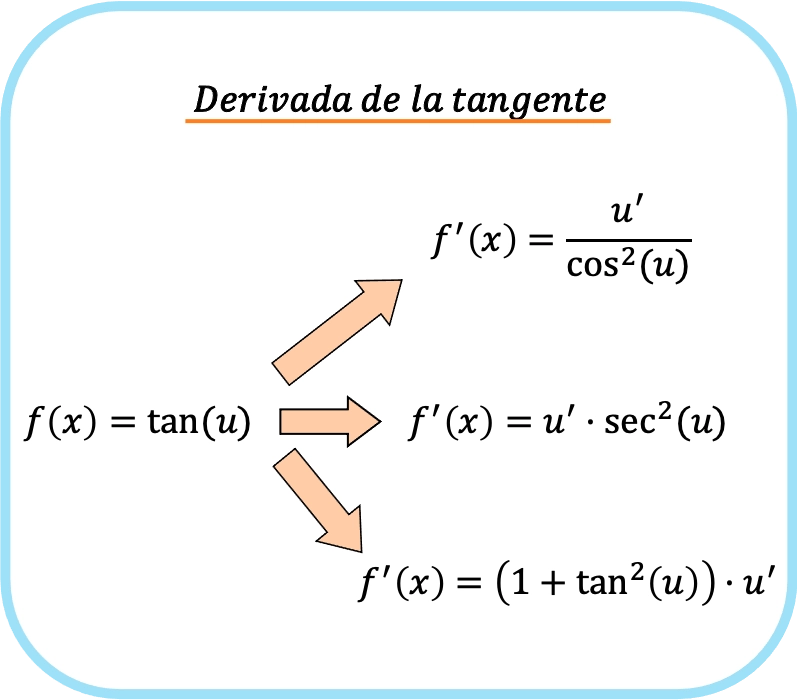
Quando invece nell’argomento tangente abbiamo una funzione diversa da x (chiamiamola u), dobbiamo applicare la regola della catena. La derivata della tangente di u è quindi:

$\begin{array}{c}f(x)=\text{tan}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cos}^2(u)}=\text{sec}^2(u)\cdot u'=\left(1+\text{tan}^2(u)\right)\cdot u'\end{array}$

In breve, la regola della derivata tangente può essere riassunta come segue:

Esempi di derivata tangente

Data la formula della derivata tangente, in questa sezione risolveremo diversi esempi di questo tipo di derivate trigonometriche in modo che tu possa capire come derivare la funzione tangente.

Esempio 1: Derivata della tangente di 2x

$f(x)=\text{tan}(2x)$

Per calcolare la derivata della tangente puoi utilizzare una delle tre formule che abbiamo visto sopra. In questo caso utilizzeremo la formula del coseno:

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

La funzione 2x è lineare, quindi la sua derivata è 2. Quindi la derivata della tangente di 2x è 2 fratto il quadrato del coseno di 2x:

$f(x)=\text{tan}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{\text{cos}^2(2x)}$

Esempio 2: Derivata della tangente di x al quadrato

$f(x)=\text{tan}(x^2)$

In questo esempio, la funzione argomento tangente non è una x, ma una funzione con una derivata. Ciò significa che dobbiamo applicare la regola della catena per ricavarlo.

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

La derivata di x al quadrato è 2x, quindi la derivata della tangente di x ² è:

$f(x)=\text{tan}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{\text{cos}^2(x^2)}$

Esempio 3: Derivata della tangente al cubo

$f(x)=\text{tan}^3(9x^2-4x)$

In questo problema abbiamo una funzione composta, quindi dovremo utilizzare anche la regola della catena per differenziare la tangente.

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

Inoltre la tangente viene elevata alla potenza di 3, il che significa che prima di applicare la formula per la derivata della tangente è necessario utilizzare la formula per la derivata di una potenza:

$\begin{aligned}f'(x)&=3\text{tan}^2(9x^2-4x)\cdot \cfrac{18x-4}{\text{cos}^2(9x^2-4x)} \\[2ex]&=\cfrac{3\text{tan}^2(9x^2-4x)\cdot(18x-4)}{\text{cos}^2(9x^2-4x)}\end{aligned}$

Derivata della tangente inversa

Come ogni funzione inversa, anche la funzione tangente ha una funzione inversa, la funzione arcotangente. Anche se la formula per ricavarla non è simile alla formula della tangente, ve la mostriamo perché può essere utile in alcuni casi.

La derivata dell’arcotangente di una funzione è il quoziente della derivata della funzione diviso per uno più detta funzione al quadrato

$f(x)=\text{tan}^{-1}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

Ad esempio, la derivata della tangente inversa di 3x è:

$f(x)=\text{tan}^{-1}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3}{1+(3x)^2}=\cfrac{3}{1+9x^2}$

Esercizi risolti sulla derivata della tangente

Calcolare la derivata delle seguenti funzioni tangenti:

$\text{A) } f(x)=\text{tan}(3x)$

$\text{B) } f(x)=\text{tan}(x^3-10x^2+8)$

$\text{C) } \displaystyle f(x)=\text{tan}^2\left(\frac{x}{2}\right)$

$\text{D) } f(x)=\text{tan}\left(e^{2x}\right)$

$\text{E) } f(x)=\text{tan}\bigl(\ln(4x)\bigr)$

$\text{F) } f(x)=\text{tan}\left(\sqrt{3x}\right)$

Vedi la soluzione

$\text{A) } f'(x)=\cfrac{3}{\text{cos}^2(3x)}$

$\text{B) } f'(x)=\cfrac{3x^2-20x}{\text{cos}^2(x^3-10x^2+8)}$

$\text{C) } \displaystyle f'(x)=2\text{tan}\left(\frac{x}{2}\right)\cdot \frac{1}{\text{cos}^2\left(\frac{x}{2}\right)}\cdot \frac{1}{2}=\frac{\text{tan}\left(\frac{x}{2}\right)}{\text{cos}^2\left(\frac{x}{2}\right)}$

$\text{D) } f'(x)=\cfrac{2e^{2x}}{\text{cos}^2(e^{2x})}$

$\text{E) } f'(x)=\cfrac{\frac{4}{4x}}{\text{cos}^2\bigl(\ln(4x)\bigr)}=\cfrac{1}{x\cdot\text{cos}^2\bigl(\ln(4x)\bigr)}$

$\text{F) } f'(x)=\cfrac{\frac{3}{2\sqrt{3x}}}{\text{cos}^2\left(\sqrt{3x}\right)}=\cfrac{3}{2\sqrt{3x}\cdot \text{cos}^2\left(\sqrt{3x}\right)}$

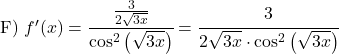
Dimostrazione della derivata della tangente

Affinché tu possa verificare che non si tratta di un’espressione inventata, in questa sezione dimostreremo la formula per la derivata della tangente utilizzando la definizione matematica di tangente.

Per fare ciò partiremo dall’identità trigonometrica che collega i tre rapporti trigonometrici:

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}$

Se usiamo la formula per la derivata di una divisione , la derivata sarebbe:

$\displaystyle\left(\text{tan}(x)\right)'=\left(\frac{\text{sen}(x)}{\text{cos}(x)}\right)'$

$\text{tan}'(x)=\cfrac{\text{cos}(x)\cdot \text{cos}(x)+\text{sen}(x)\text{sen}(x) }{\text{cos}^2(x)}$

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)+\text{sen}^2(x)}{\text{cos}^2(x)}$

Ma, utilizzando l’identità trigonometrica fondamentale, sappiamo che il quadrato del seno più il quadrato del coseno è 1:

$\text{sen}^2(x)+\text{cos}^2(x)=1$

$\text{tan}'(x)=\cfrac{1}{\text{cos}^2(x)}$

E così siamo già arrivati alla prima formula per la derivata della tangente. Inoltre, la secante è l’inverso moltiplicativo del coseno, quindi si deriva anche la seconda espressione:

$\text{tan}'(x)=\text{sec}^2(x)$

Infine, la terza regola della derivata tangente può essere dimostrata trasformando la frazione del passaggio precedente in una somma di frazioni:

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)+\text{sen}^2(x)}{\text{cos}^2(x)}$

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)}{\text{cos}^2(x)}+\cfrac{\text{sen}^2(x)}{\text{cos}^2(x)}$

$\text{tan}'(x)=1+\text{tan}^2(x)$

Qual è la derivata della tangente?

Esempi di derivata tangente

Esempio 1: Derivata della tangente di 2x

Esempio 2: Derivata della tangente di x al quadrato

Esempio 3: Derivata della tangente al cubo

Derivata della tangente inversa

Esercizi risolti sulla derivata della tangente

Dimostrazione della derivata della tangente

Lascia un commento Annulla risposta