In questo articolo spieghiamo come ricavare la secante iperbolica di una funzione. Troverai la formula della derivata della secante iperbolica e diversi esempi pratici di questo tipo di derivata.
Formula per la derivata della secante iperbolica
La derivata della secante iperbolica di x è uguale a meno il prodotto della secante iperbolica di x per la tangente iperbolica di x.
![]()
Pertanto, la derivata della secante iperbolica di una funzione è meno il prodotto della secante iperbolica della funzione per la tangente iperbolica della funzione per la derivata di detta funzione.
![]()
In breve, la formula per la derivata della funzione secante iperbolica è:
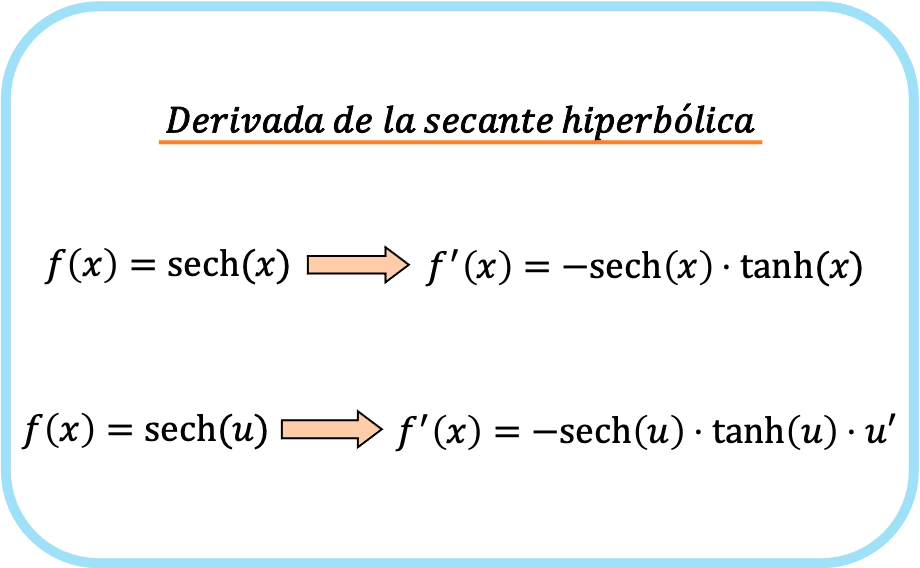
Tieni presente che entrambe le espressioni appartengono in realtà a un’unica formula. L’unica differenza è che nella seconda formula viene applicata la regola della catena.
Esempi di derivata della secante iperbolica
Ora che conosciamo la formula per la derivata della secante iperbolica, vedremo diversi esercizi risolti di questo tipo di derivata trigonometrica.
Esempio 1
![]()
In questo esempio abbiamo una funzione diversa da x nell’argomento secante iperbolica, quindi per ricavarla dobbiamo utilizzare la formula della regola della catena.
![]()
Poiché la funzione 2x è lineare, la sua derivata è 2. Pertanto, per trovare la derivata, sostituiamo semplicemente u con 2x e u’ con 2 nella formula:
![]()
Esempio 2
![]()
La funzione di questo esercizio è composta, poiché la secante iperbolica ha un’altra funzione nel suo argomento. Dobbiamo quindi utilizzare la formula della secante iperbolica con la regola della catena per farne la derivazione:
![]()
La derivata di x elevata a 2 dà 2x, quindi la derivata della secante iperbolica di x al quadrato è:
![]()