▷ Derivata della secante (formula ed esercizi risolti)

Qui scoprirai come ricavare la secante di una funzione. Inoltre, potrai vedere diversi esercizi risolti passo dopo passo sulla derivata della secante. E infine troverai la dimostrazione della formula per questo tipo di derivata trigonometrica.

Qual è la derivata della secante?

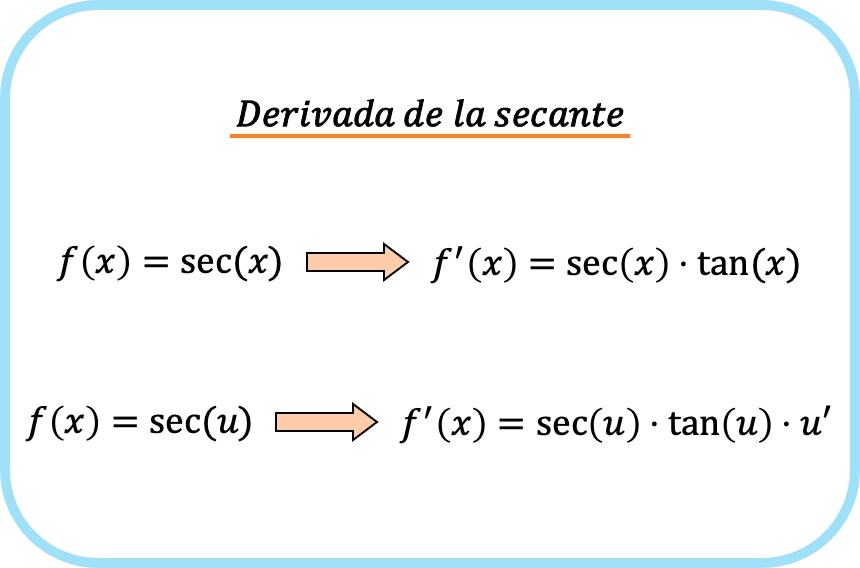
La derivata della secante di x è uguale al prodotto della secante di x e della tangente di x.

$f(x)=\text{sec}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(x)\cdot \text{tan}(x)$

Applicando formule trigonometriche, la derivata della secante di x può anche essere definita come il quoziente del seno di x diviso per il quadrato del coseno di x.

$f'(x)=\text{sec}(x)\cdot \text{tan}(x)=\cfrac{1}{\text{cos}(x)}\cdot \cfrac{\text{sen}(x)}{\text{cos}(x)}=\cfrac{\text{sen}(x)}{\text{cos}^2(x)}$

E se applichiamo la regola della catena, la derivata della secante di una funzione è il prodotto della secante della funzione per la tangente della funzione per la derivata della funzione.

$f(x)=\text{sec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(u)\cdot \text{tan}(u)\cdot u'$

In sintesi, la formula per la derivata della funzione secante è la seguente:

Esempi di derivata della secante

Una volta vista qual è la formula della derivata della secante, risolveremo diversi esempi di questo tipo di derivate trigonometriche.

Esempio 1: Derivata della secante di 2x

In questo esempio vedremo quanto vale la derivata della secante di 2x:

$f(x)=\text{sec}(2x)$

Per ricavare la secante della funzione 2x, è necessario utilizzare la formula corrispondente. Inoltre, nell’argomento secante abbiamo una funzione diversa da x, quindi dobbiamo applicare la regola della catena.

$f(x)=\text{sec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(u)\cdot \text{tan}(u)\cdot u'$

La funzione 2x è lineare, quindi la sua derivata è 2. Pertanto, per trovare la derivata, sostituiamo semplicemente u con 2x e u’ con 2 nella formula:

$f(x)=\text{sec}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(2x)\cdot \text{tan}(2x)\cdot 2$

Esempio 2: Derivata della secante di x al quadrato

In questo esercizio vedremo qual è la derivata della secante di x al quadrato:

$f(x)=\text{sec}(x^2)$

Per ricavare la secante di una funzione puoi utilizzare una delle due formule viste sopra, ma in questo caso differenzieremo la funzione con la formula della moltiplicazione tra secante e tangente.

$f(x)=\text{sec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(u)\cdot \text{tan}(u)\cdot u'$

La derivata di x elevata a 2 dà 2x, quindi la derivata della secante di x al quadrato è:

$f(x)=\text{sec}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(x^2)\cdot \text{tan}(x^2)\cdot 2x$

Esempio 3: Derivata del cubo secante di un polinomio

$f(x)=\text{sec}^3(x^5+4x^2-3)$

La regola per la derivata della secante di una funzione è:

$f(x)=\text{sec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(u)\cdot \text{tan}(u)\cdot u'$

Ma in questo caso dobbiamo derivare una funzione composta, poiché la secante è elevata alla terza potenza e, inoltre, nel suo argomento abbiamo una funzione polinomiale. Quindi, per differenziare l’intera funzione, dobbiamo applicare la regola della catena:

$\begin{aligned}f'(x)& =3\text{sec}^2(x^5+4x^2-3)\text{sec}(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\\[1.5ex]&=3\text{sec}^3(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\end{aligned}$

Esercizi risolti sulla derivata di una secante

Derivare le seguenti funzioni secanti:

$\text{A) }f(x)=\text{sec}(x^6-6x^3)$

$\text{B) }f(x)=\text{sec}^4(5x^4)$

$\text{C) }f(x)=\text{sec}\bigl(\ln(x)\bigr)$

$\text{D) }f(x)=\text{sec}\left(e^{x^2+3x}\right)$

$\text{E) }f(x)=\text{sec}\left(\sqrt{5x+1}\right)$

Vedi la soluzione

$\text{A) }f(x)=\text{sec}(x^6-6x^3)\cdot \text{tan}(x^6-6x^3)\cdot (6x^5-18x^2)$

$\begin{aligned}\text{B) }f(x)& =4\text{sec}^3(5x^4)\cdot \text{sec}(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\\[1.5ex] &=4\text{sec}^4(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\end{aligned}$

$\text{C) }f(x)=\text{sec}\bigl(\ln(x)\bigr)\cdot \text{tan}\bigl(\ln(x)\bigr)\cdot \cfrac{1}{x}$

$\text{D) }f(x)=\text{sec}\left(e^{x^2+3x}\right)\cdot \text{tan}\left(e^{x^2+3x}\right)\cdot e^{x^2+3x}\cdot (2x+3)$

$\text{E) }f(x)=\text{sec}\left(\sqrt{5x+1}\right)\cdot \text{tan}\left(\sqrt{5x+1}\right)\cdot \cfrac{5}{2\sqrt{5x+1}}$

Dimostrazione della formula per la derivata della secante

Successivamente dimostreremo la formula per la derivata della secante. Anche se ovviamente non è necessario conoscere la dimostrazione a memoria, è sempre bene capire da dove provengono le formule.

Matematicamente, la definizione di secante è l’inverso moltiplicativo del coseno:

$f(x)=\text{sec}(x)=\cfrac{1}{\text{cos}(x)}$

Possiamo quindi provare a ricavare la secante utilizzando la regola del quoziente:

$f'(x)=\cfrac{\text{sen}(x)}{\text{cos}^2(x)}$

E, come abbiamo visto nella prima sezione, l’espressione precedente può essere convertita nella formula della derivata della secante. Per fare ciò, separiamo la frazione in due frazioni diverse:

$f'(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}\cdot \cfrac{1}{\text{cos}(x)}$

La divisione del seno per il coseno equivale alla tangente, sostituiamo quindi detto quoziente con la tangente:

$f'(x)=\text{tan}(x)\cdot \cfrac{1}{\text{cos}(x)}$

Secondo la definizione matematica della funzione secante, il coseno è il suo moltiplicativo inverso. Quindi sostituendo uno diviso per il coseno con la secante si arriva alla formula della sua derivata:

$f'(x)=\text{tan}(x)\cdot \text{sec}(x)$

Qual è la derivata della secante?

Esempi di derivata della secante

Esempio 1: Derivata della secante di 2x

Esempio 2: Derivata della secante di x al quadrato

Esempio 3: Derivata del cubo secante di un polinomio

Esercizi risolti sulla derivata di una secante

Dimostrazione della formula per la derivata della secante

Lascia un commento Annulla risposta