▷ Derivata della cotangente (formula ed esempi)

In questo articolo vedremo come ricavare la cotangente di una funzione. Troverai esempi di derivata della cotangente e anche esercizi risolti passo dopo passo. Infine, dimostriamo la formula per la derivata della cotangente.

Formula per la derivata della cotangente

La derivata della cotangente di x è uguale a uno negativo sul quadrato del seno di x. Anche la derivata della cotangente di x è uguale a meno il quadrato della cosecante di x e meno la somma di uno più il quadrato della cotangente di x.

$\begin{array}{c}f(x)=\text{cotg}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=-\cfrac{1}{\text{sen}^2(x)}=-\text{cosec}^2(x)=-\left(1+\text{cotg}^2(x)\right)\end{array}$

Se la cotangente dell’argomento è una funzione diversa da x, le formule per la derivata della cotangente di una funzione sono le stesse delle precedenti, ma moltiplicando le espressioni per la derivata della funzione dell’argomento.

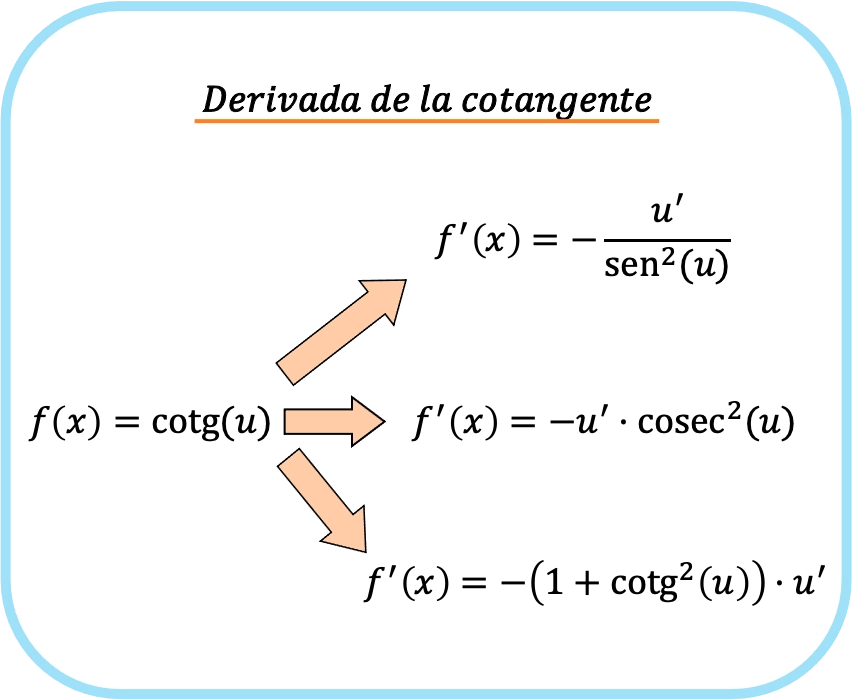
$\begin{array}{c}f(x)=\text{cotg}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=-\cfrac{u'}{\text{sen}^2(u)}=-u' \cdot \text{cosec}^2(u)=-u' \cdot \left(1+\text{cotg}^2(u)\right)\end{array}$

Ciò significa che esistono tre diverse formule per trovare la derivata della cotangente. Ma, logicamente, non è necessario utilizzare tutte e tre le formule, ma potete derivarlo con la formula che preferite.

Esempi di derivata della cotangente

Ora che abbiamo visto la formula per la derivata della cotangente di una funzione, in questa sezione risolveremo diversi esempi di questo tipo di derivate trigonometriche.

Esempio 1: Derivata della cotangente di 2x

In questo esempio vedremo qual è la derivata della cotangente della funzione 2x.

$f(x)=\text{cotg}(2x)$

Come abbiamo visto, per calcolare la derivata della cotangente si può utilizzare una delle tre formule viste sopra. In questo caso utilizzeremo la formula sinusoidale:

$f(x)=\text{cotg}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\text{sen}^2(u)}$

Poiché 2x è un termine di primo grado, la sua derivata è 2. Quindi la derivata della cotangente di 2x è negativa due diviso per il quadrato del seno di 2x:

$f(x)=\text{cotg}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2}{\text{sen}^2(2x)}$

Esempio 2: Derivata della cotangente di x al quadrato

Nel secondo esempio determineremo qual è la derivata della cotangente di x al quadrato.

$f(x)=\text{cotg}(x^2)$

In questo esempio, la funzione dell’argomento cotangente non è una x, quindi dobbiamo applicare la regola della catena per differenziare la cotangente.

$f(x)=\text{cotg}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\text{sen}^2(u)}$

La derivata di x al quadrato è 2x, quindi la derivata della cotangente di x ² è:

$f(x)=\text{cotg}(x^2)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{\text{sen}^2(x^2)}$

Esempio 3: Derivata della cotangente al cubo

Infine, troveremo quanto vale la derivata della cotangente al cubo di una funzione polinomiale:

$f(x)=\text{cotg}^3(x^5-6x^2+10)$

In questo caso abbiamo una composizione di funzioni, quindi dobbiamo usare la regola della catena con la formula per la derivata di una potenza per trovare la derivata della cotangente:

$\displaystyle f'(x)=-3\cdot\text{cotg}^2(x^5-6x^2+10)\cdot\frac{5x^4-12x}{\text{sen}^2(x^5-6x^2+10)}$

Esercizi risolti sulla derivata della cotangente

Calcolare la derivata delle seguenti funzioni cotangenti:

$\text{A) } f(x)=\text{cotg}(5x)$

$\text{B) } f(x)=\text{cotg}(2x^4+10x-3)$

$\text{C) } \displaystyle f(x)=\text{cotg}^5\left(\frac{x}{2}\right)$

$\text{D) } f(x)=\text{cotg}\left(e^{x^2}\right)$

$\text{E) } f(x)=\text{cotg}\bigl(\ln(x^2)\bigr)$

$\text{F) } f(x)=\text{cotg}\left(\sqrt{8x}\right)$

Vedi la soluzione

$\text{A) } f'(x)=-\cfrac{5}{\text{sen}^2(5x)}$

$\text{B) } f'(x)=-\cfrac{8x+10}{\text{sen}^2(2x^4+10x-3)}$

$\text{C) } \displaystyle f'(x)=5\cdot \text{cotg}^4\left(\frac{x}{2}\right)\cdot \left(-\frac{1}{\text{sen}^2\left(\frac{x}{2}\right)}\right)\cdot \frac{1}{2}=-\frac{5\cdot \text{cotg}^4\left(\frac{x}{2}\right)}{2\cdot \text{sen}^2\left(\frac{x}{2}\right)}$

$\text{D) } f'(x)=-\cfrac{2x\cdot e^{x^2}}{\text{sen}^2(e^{x^2})}$

$\text{E) } f'(x)=-\cfrac{\cfrac{2x}{x^2}}{\text{sen}^2\bigl(\ln(x^2)\bigr)}=-\cfrac{2}{x\cdot\text{sen}^2\bigl(\ln(x^2)\bigr)}$

$\text{F) } f'(x)=-\cfrac{\frac{8}{2\sqrt{8x}}}{\text{sen}^2\left(\sqrt{8x}\right)}=-\cfrac{4}{\sqrt{8x}\cdot \text{sen}^2\left(\sqrt{8x}\right)}$

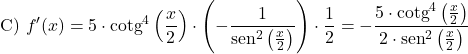
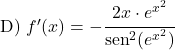
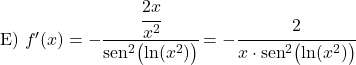
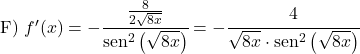
Dimostrazione della derivata della cotangente

In questa sezione finale, dimostreremo la formula per la derivata della cotangente. Per fare ciò partiremo dalla definizione matematica della funzione cotangente, che è uguale al coseno diviso il seno:

$\text{cotg}(x)=\cfrac{\text{cos}(x)}{\text{sen}(x)}$

Ora differenziamo la funzione applicando la regola della derivata di un quoziente;

$\displaystyle\bigl(\text{cotg}(x)\bigr)'=\left(\frac{\text{cos}(x)}{\text{sen}(x)}\right)'$

$\text{cotg}'(x)=\cfrac{-\text{sen}(x)\cdot \text{sen}(x)-\text{cos}(x)\cdot \text{cos}(x) }{\text{sen}^2(x)}$

$\text{cotg}'(x)=\cfrac{-\text{sen}^2(x)-\text{cos}^2(x)}{\text{sen}^2(x)}$

Prendiamo il fattore comune al denominatore e rimuoviamo il segno negativo dalla frazione:

$\text{cotg}'(x)=\cfrac{-\bigl(\text{sen}^2(x)+\text{cos}^2(x)\bigr)}{\text{sen}^2(x)}$

$\text{cotg}'(x)=-\cfrac{\text{sen}^2(x)+\text{cos}^2(x)}{\text{sen}^2(x)}$

Sappiamo invece che il quadrato del seno più il quadrato del coseno è uguale a uno grazie all’identità trigonometrica fondamentale.

$\text{sen}^2(x)+\text{cos}^2(x)=1$

$\text{cotg}'(x)=-\cfrac{1}{\text{sen}^2(x)}$

E abbiamo così ottenuto la prima formula della derivata della cotangente. Allo stesso modo, la cosecante è l’inverso moltiplicativo del seno, quindi è dimostrata anche la seconda regola della derivata della cotangente:

$\text{cotg}'(x)=-\text{sec}^2(x)$

Infine, la terza formula per la derivata di questa funzione trigonometrica può essere dimostrata trasformando la frazione del passaggio precedente in una somma di frazioni: