In questo articolo spieghiamo come derivare la cosecante iperbolica di una funzione. Inoltre, potrai vedere diversi esempi risolti della derivata della cosecante iperbolica.
Formula per la derivata della cosecante iperbolica
La derivata della cosecante iperbolica di x è uguale a meno la cosecante iperbolica di x moltiplicata per la cotangente iperbolica di x.
![]()
Pertanto, la derivata della cosecante iperbolica di una funzione è meno il prodotto della cosecante iperbolica della funzione per la cotangente iperbolica della funzione per la derivata di detta funzione.
![]()
In breve, la formula per derivare la cosecante di una funzione è:
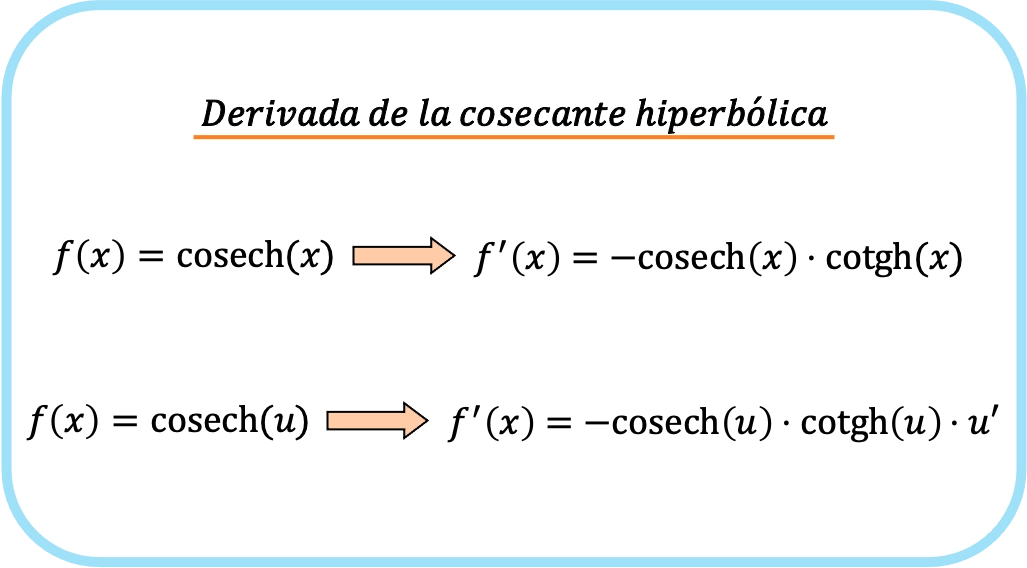
Infatti le due espressioni precedenti corrispondono ad un’unica formula, la differenza è che nella seconda formula viene applicata la regola della catena.
Esempi di derivata della cosecante iperbolica
Dopo aver visto qual è la formula per la derivata della cosecante iperbolica, ecco alcuni esempi pratici di questo tipo di derivata trigonometrica.
Esempio 1
In questo primo esempio deriveremo la cosecante iperbolica di x al quadrato:
![]()
La funzione dell’argomento della cosecante iperbolica è diversa da x, quindi dobbiamo usare la formula per la derivata della cosecante iperbolica con la regola della catena.
![]()
Quindi, per derivare questa funzione trigonometrica, dobbiamo semplicemente sostituire i valori nella formula precedente, cioè nell’argomento della cosecante iperbolica e della tangente iperbolica, mettiamo x 2 , e moltiplichiamo il tutto per la derivata di x al quadrato, che è 2x:
![]()
Esempio 2
In questo esercizio vedremo quanto vale la derivata della cosecante iperbolica di x cubica:
![]()
Per trovare la derivata della cosecante iperbolica di una funzione, applichiamo la sua formula:
![]()
La derivata di x al cubo è 3x 2 , quindi la derivata dell’intera funzione è:
![]()