Derivato del seno iperbolico

Qui troverai come ricavare il seno iperbolico (formula). Inoltre, vedrai diversi esempi risolti della derivata del seno iperbolico. Infine, dimostriamo la formula per la derivata di questo tipo di funzione trigonometrica.

Formula derivata dal seno iperbolico

La derivata del seno iperbolico di x è il coseno iperbolico di x.

$f(x)=\text{senh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(x)$

Pertanto, la derivata del seno iperbolico di una funzione è uguale al prodotto del coseno iperbolico della funzione e della derivata di quella funzione.

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

In realtà le due formule precedenti sono identiche, l’unica differenza è che nella seconda formula applichiamo la regola della catena. E poiché la derivata di x è 1, ciò non cambia la funzione.

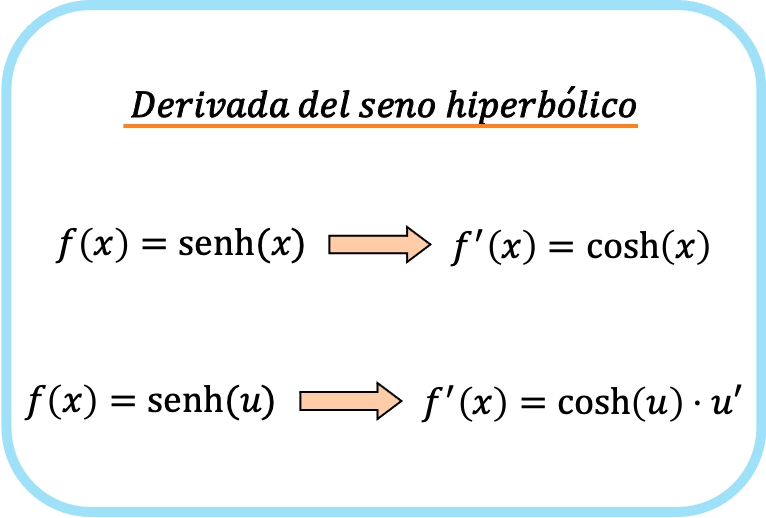
Come puoi vedere, la formula per la derivata del seno iperbolico è molto simile alla formula per la derivata del seno .

Esempi di derivata del seno iperbolico

Una volta che abbiamo già visto cos’è la formula della derivata del seno iperbolico, procediamo ora a risolvere alcuni esempi della derivata del seno iperbolico. Quindi sicuramente non hai dubbi su come farlo.

Esempio 1: Derivata del seno iperbolico di 2x

$f(x)=\text{senh}(2x)$

In questo caso, nell’argomento del seno iperbolico, abbiamo una funzione diversa da x, quindi dobbiamo usare la formula della derivata del seno iperbolico con la regola della catena per trovare la derivata:

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

La derivata di 2x è 2, quindi la derivata del seno iperbolico di 2x sarà il coseno iperbolico di 2x per 2.

$f(x)=\text{senh}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(2x)\cdot 2=2\text{cosh}(2x)$

Esempio 2: Derivata del seno iperbolico di x al quadrato

$f(x)=\text{senh}(x^2)$

La formula per la derivata della funzione seno iperbolico è:

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

D’altra parte, la derivata della funzione quadratica x ² è 2x. La derivata dell’intera funzione è quindi:

$f(x)=\text{senh}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(x^2)\cdot 2x$

Dimostrazione della formula della derivata del seno iperbolico

Infine, dimostreremo la formula per la derivata del seno iperbolico. Per fare ciò partiremo dalla definizione matematica di seno iperbolico:

$\text{senh}(x)=\cfrac{e^x-e^{-x}}{2}$

Deduciamo ora i due lati dell’uguaglianza:

$\displaystyle\bigl(\text{senh}(x)\bigr)'=\left(\frac{e^x-e^{-x}}{2}\right)'$

Per ricavare la parte destra dell’equazione, utilizzeremo la formula per la derivata della divisione:

$\displaystyle\text{senh}'(x)=\frac{(e^x+e^{-x})\cdot 2}{2^2}=\frac{e^x+e^{-x}}{2}$

➤ Vedi: derivata della funzione esponenziale con base e

E proprio siamo arrivati all’espressione che definisce il coseno iperbolico. Pertanto risulta dimostrata la derivata del seno iperbolico:

$\displaystyle\text{senh}'(x)=\text{cosh}(x)$

Formula derivata dal seno iperbolico

Esempi di derivata del seno iperbolico

Esempio 1: Derivata del seno iperbolico di 2x

Esempio 2: Derivata del seno iperbolico di x al quadrato

Dimostrazione della formula della derivata del seno iperbolico

Lascia un commento Annulla risposta