Derivato della cosecante

In questo articolo spieghiamo come ricavare la cosecante di una funzione (formula). Troverai anche esercizi risolti passo passo per la derivata della cosecante. E infine potrai vedere la dimostrazione della formula per questo tipo di derivata trigonometrica.

Formula del derivato cosecante

La derivata della cosecante di x è uguale a meno il quoziente del coseno di x diviso per il seno quadrato di x.

$f(x)=\text{cosec}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{\text{cos}(x)}{\text{sen}^2(x)}$

Usando le formule trigonometriche, possiamo anche definire la derivata della cosecante di x come meno il prodotto della cotangente di x per la cosecante di x.

$f'(x)=-\cfrac{\text{cos}(x)}{\text{sen}^2(x)}=-\cfrac{\text{cos}(x)}{\text{sen}(x)}\cdot \cfrac{1}{\text{sen}(x)}=-\text{cot}(x)\cdot \text{cosec}(x)$

E se applichiamo la regola della catena, la derivata della cosecante di una funzione è meno il prodotto della derivata della funzione per il coseno della funzione, diviso per il seno quadrato della funzione.

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

La formula utilizzata per ricavare la cosecante di una funzione è quindi la seguente:

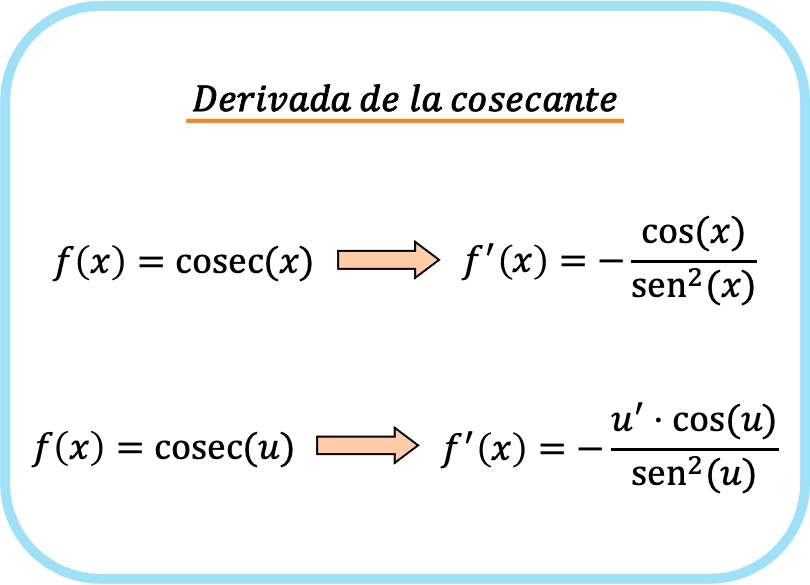
Esempi di derivata della cosecante

Avendo visto qual è la formula della derivata della cosecante, faremo ora alcuni esempi. Quindi puoi vedere esattamente come viene derivata la cosecante di una funzione.

Esempio 1: Derivata della cosecante di 2x

In questo esempio vedremo quanto vale la derivata della cosecante di 2x:

$f(x)=\text{cosec}(2x)$

La funzione argomento cosecante è diversa da x, quindi dobbiamo utilizzare la regola della derivata cosecante con la regola della catena.

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

Quindi, per trovare la derivata di questa funzione trigonometrica, basta sostituire i valori della formula precedente: nell’argomento coseno e seno mettiamo 2x, e u’ corrisponde alla derivata di 2x, cioè 2:

$f(x)=\text{cosec}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2\cdot \text{cos}(2x)}{\text{sen}^2(2x)}$

Esempio 2: Derivata della cosecante di x al quadrato

In questo esercizio vedremo quanto vale la derivata della cosecante di x al quadrato:

$f(x)=\text{cosec}(x^2)$

Logicamente, la derivata di questa funzione trigonometrica si risolve utilizzando la formula per la derivata della cosecante:

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

La derivata di x al quadrato dà 2x, quindi la derivata della cosecante di x elevata a due è:

$f(x)=\text{cosec}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x\cdot \text{cos}(x^2)}{\text{sen}^2(x^2)}$

Esempio 3: Derivata della cosecante al cubo di una funzione esponenziale

$f(x)=\text{cosec}^3(e^{5x})$

Qualunque sia l’argomento della funzione, la regola per la derivata della cosecante di una funzione è:

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

Ma in questo caso abbiamo una funzione composta, perché la cosecante è elevata a tre e, inoltre, nel suo argomento c’è una funzione esponenziale. Quindi, per differenziare l’intera funzione, dobbiamo applicare più volte la regola della catena:

$\begin{aligned}\displaystyle f'(x)& = 3\text{cosec}^2(e^{5x})\cdot\left(-\frac{5e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\right)\\[1.5ex]&=-\frac{-15\text{cosec}^2(e^{5x})\cdot e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\end{aligned}$

Risolti problemi della derivata della cosecante

Derivare le seguenti funzioni cosecanti:

$\text{A) }f(x)=\text{cosec}(x^4-2x^2)$

$\text{B) }f(x)=\text{cosec}(x^3+e^x-10)$

$\text{C) }f(x)=\text{cosec}\bigl(\ln(x^3+7x^2)\bigr)$

$\text{D) }f(x)=\text{cosec}\bigl(\text{arccos}(x^7)\bigr)$

$\text{E) }f(x)=\text{cosec}\left(\sqrt{9x^2-4x}\right)$

vedi soluzione

$\text{A) }f('x)=-\cfrac{(4x^3-4x)\cdot \text{cos}(x^4-2x^2)}{\text{sen}^2(x^4-2x^2)}$

$\text{B) }f('x)=-\cfrac{(3x^2+e^x)\cdot \text{cos}(x^3+e^x-10)}{\text{sen}^2(x^3+e^x-10)}$

$\begin{aligned}\text{C) }f'(x)& =-\cfrac{\cfrac{3x^2+14x}{x^3+7x^2}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{\cfrac{3x+14}{x^2+7x}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{(3x+14)\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{(x^2+7x)\cdot \text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\end{aligned}$

$\begin{aligned}\text{D) }f'(x)& =-\cfrac{-\cfrac{7x^6}{\sqrt{1-\left(x^7\right)^2}}\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =-\cfrac{(-7x^6)\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =\cfrac{7x^6\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\end{aligned}$

$\begin{aligned} \text{E) }f'(x)& =-\cfrac{\cfrac{18x-4}{2\cdot\sqrt{9x^2-4x}} \cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{\text{sen}^2\left(\sqrt{9x^2-4x}\right)}\\[1.5ex] &=-\cfrac{(18x-4)\cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{2\sqrt{9x^2-4x}\cdot \text{sen}^2\left(\sqrt{9x^2-4x}\right)} \end{aligned}$

Dimostrazione della formula della derivata della cosecante

Successivamente dimostreremo la formula per la derivata della cosecante. A differenza di altre dimostrazioni, in questo caso non utilizzeremo il limite che definisce una derivata, ma partiremo dalla definizione matematica della cosecante.

Algebricamente, la funzione trigonometrica cosecante è l’inverso moltiplicativo del seno:

$f(x)=\text{cosec}(x)=\cfrac{1}{\text{sen}(x)}$

Possiamo quindi ricavare la derivata della cosecante utilizzando la regola del quoziente:

$f'(x)=\cfrac{0\cdot \text{sen}(x)-1\cdot \text{cos}(x)}{\text{sen}^2(x)}$

$f'(x)=\cfrac{-\text{cos}(x)}{\text{sen}^2(x)}$

Come puoi vedere, è solo applicando la regola della derivata di una divisione che arriviamo alla formula della derivata della cosecante. E poiché la derivata di un quoziente è già dimostrata (puoi vederla nel link seguente), anche la regola della derivata cosecante è dimostrata.

➤ Vedi: dimostrazione della derivata di un quoziente

Formula del derivato cosecante

Esempi di derivata della cosecante

Esempio 1: Derivata della cosecante di 2x

Esempio 2: Derivata della cosecante di x al quadrato

Esempio 3: Derivata della cosecante al cubo di una funzione esponenziale

Risolti problemi della derivata della cosecante

Dimostrazione della formula della derivata della cosecante

Lascia un commento Annulla risposta