Linee parallele - Mathority

Qui troverai tutto sulle rette parallele: cosa significano, come determinare se due rette sono parallele, le loro proprietà, ecc. Inoltre, potrai vedere diversi esempi ed esercizi risolti di rette parallele.

Cosa sono le rette parallele?

Le rette parallele sono quelle che non si incrociano mai, vale a dire che, anche se le loro traiettorie si prolungano all’infinito, non si toccano mai. Pertanto i punti di due rette parallele sono sempre alla stessa distanza l’uno dall’altro e, inoltre, due rette parallele non hanno punti in comune.

Ad esempio, le seguenti due rette sono parallele:

Generalmente indichiamo che due linee sono parallele a 2 barre verticali || tra le linee

D’altra parte, nonostante due linee parallele non si intersechino mai, in geometria analitica diciamo che formano un angolo di 0º poiché hanno la stessa direzione.

Quando due rette sono parallele?

Una volta vista la definizione di rette parallele, vedremo come trovare due rette parallele. Ovviamente un modo sarebbe quello di rappresentare graficamente le linee e vedere se si intersecano sul grafico, ma esistono metodi ancora più semplici e facili da usare.

Determina il parallelismo di due rette con le loro pendenze

Puoi capire quando due rette sono parallele osservando la pendenza di ciascuna retta. Ricorda che il parametro è la pendenza di una linea

$m$

dall’equazione esplicita e dall’equazione punto-pendenza della retta:

$y=mx+n \qquad \qquad y-y_0=m(x-x_0)$

Esistono però diversi modi per determinare la pendenza di una retta, quindi per scoprire come calcolarla ti consigliamo di dare un’occhiata alla formula della pendenza di una retta . Inoltre, nella pagina collegata troverai anche una spiegazione di cosa rappresenta la pendenza di una linea e perché è così importante per una linea.

Pertanto, nel piano, due rette sono parallele se hanno la stessa pendenza (coefficiente m) e diverse ordinate nell’origine (coefficiente n) .

Ad esempio, le seguenti due rette sono parallele:

$r: \ y=5x+1 \qquad \qquad s: \ y=5x-3$

Sono due rette parallele perché hanno entrambe la stessa pendenza e inoltre i loro termini indipendenti sono diversi.

$m_r =m_s =5$

$n_r =1 \neq n_s =-3$

È da notare che se due rette avessero la stessa pendenza e allo stesso tempo lo stesso computer all’origine, sarebbero rette identiche perché sarebbero esattamente identiche.

Trova il parallelismo di due rette dall’equazione implicita

Ricorda che l’equazione implicita (o generale) della retta è:

$Ax+By+C=0$

Quindi, se i coefficienti A e B di due rette sono proporzionali tra loro ma non al coefficiente C , ciò significa che le rette sono parallele.

$r: \ Ax+By+C=0 \qquad \qquad s: \ A'x+B'y+C'=0$

$\cfrac{A}{A'} = \cfrac{B}{B'} \neq \cfrac{C}{C'} \quad \bm{\longrightarrow} \quad r \parallel s$

Ecco due linee parallele espresse nella forma di un’equazione generale (o implicita):

$r: \ 4x-6y+7=0 \qquad \qquad s: \ -2x+3y-1=0$

Sono paralleli perché i numeri davanti alla variabile

$x$

sono proporzionali ai numeri davanti alla variabile

$y$

, ma non con termini indipendenti.

$\cfrac{4}{-2} = \cfrac{-6}{3} = -2 \neq \cfrac{7}{-1}=-7$

Come prima, se tutti i coefficienti (A, B e C) di due linee implicite fossero proporzionali, ciò implicherebbe che le due linee coincidono, o in altre parole, che sono uguali.

Proprietà delle rette parallele

Le caratteristiche delle rette parallele sono le seguenti:

Proprietà simmetrica : se una retta è parallela ad un’altra, anche questa retta sarà parallela alla prima. Questa proprietà è posseduta anche dalle linee perpendicolari.

$r \parallel s \ \longrightarrow \ s \parallel r$

Proprietà transitiva : se una linea è parallela ad un’altra linea, e questa seconda linea è parallela ad una terza linea, anche la prima linea è parallela alla terza linea.

$\left. \begin{array}{c} r \parallel s\\[2ex] s \parallel q \end{array} \right\} \longrightarrow \ r \parallel q$

Il prodotto scalare dei vettori di direzione (vettore che indica la direzione di una retta) di due rette parallele è pari al prodotto dei loro moduli.

$r \parallel s \ \longrightarrow \ \vv{\text{v}}_r \cdot \vv{\text{v}}_s= \lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{\text{v}}_s \rvert$

Inoltre i vettori di direzione di due rette parallele sono sempre linearmente dipendenti l’uno dall’altro, poiché sono proporzionali .

Questa condizione è necessaria affinché le rette siano parallele ma non sufficiente, ovvero due rette parallele devono avere vettori di direzione proporzionali, ma il fatto che due rette abbiano vettori di direzione proporzionali non implica direttamente che siano parallele. Poiché le linee coincidenti hanno anche vettori di direzione proporzionali.

Le linee parallele all’asse delle ascisse (asse X) sono orizzontali e hanno sempre la forma
$y=k.$

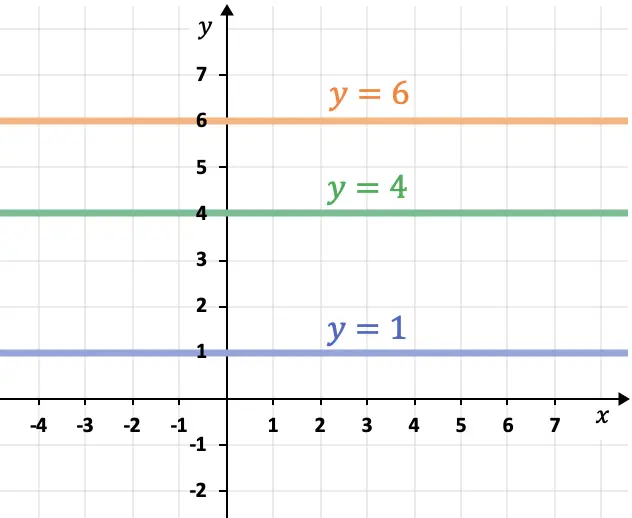
Le linee parallele all’asse del computer (asse Y) sono verticali e seguono sempre l’espressione
$x=k.$

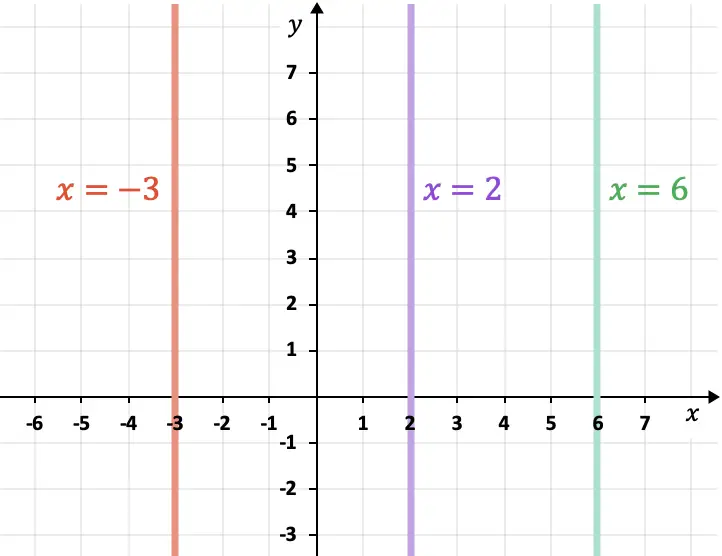
Come calcolare la distanza tra due rette parallele nel piano

Per trovare la distanza tra due linee parallele nel piano (in R2), basta prendere un punto su una delle due linee e calcolare la distanza da questo punto all’altra linea.

Possiamo farlo in questo modo perché due linee parallele sono sempre alla stessa distanza.

D’altra parte, se utilizzando la formula otteniamo una distanza di 0 unità, ciò significa che le linee si toccano in un punto e, quindi, le linee non sono parallele, ma si intersecano, coincidenti o perpendicolari. Se vuoi, puoi verificare le differenze tra questo tipo di linee sul nostro sito.

Quindi, affinché tu possa vedere come si fa, determineremo come esempio la distanza tra le seguenti due linee parallele:

$r: \ 2x-4y-6=0 \qquad \qquad s: \ -x+2y+4=0$

La prima cosa che dobbiamo fare è ottenere un punto su una delle linee (quella che desideri). In questo caso, calcoleremo un punto sulla linea

$s.$

Per fare ciò, dobbiamo dare un valore a una delle variabili, faremo ad esempio

$x=0:$

$-x+2y+4 =0 \ \xrightarrow{x \ = \ 0} \ -0+2y+4=0$

E ora cancelliamo l’altra variabile (

$y$

) dell’equazione ottenuta per sapere quanto vale a questo punto:

$2y=-4$

$y= \cfrac{-4}{2}$

$y= -2$

Pertanto il punto ottenuto dalla retta

$s$

Est:

$P(0,-2)$

E una volta che abbiamo già un punto su una linea, calcoliamo la distanza da quel punto all’altra linea utilizzando la formula per la distanza da un punto a una linea:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 2\cdot 0 + (-4)\cdot (-2) +(-6)\rvert}{\sqrt{2^2+(-4)^2}}= \cfrac{\lvert 0+8-6\rvert}{\sqrt{4+16}}={\cfrac{2}{\sqrt{20}}=\bm{0,45}$

La distanza tra le due linee parallele equivale quindi a 0,45 unità .

Problemi risolti delle linee parallele

Esercizio 1

Quali delle seguenti rette sono parallele?

$\begin{array}{l} r: \ y=2x+3 \\[2ex] s: \ y=3x-2 \\[2ex] q: \ y=2x+6 \\[2ex] t: \ y=-2x-4\end{array}$

vedi soluzione

Due rette sono parallele se hanno la stessa pendenza (e intercetta diversa). Pertanto la pendenza di ciascuna retta è:

$m_r = 2$

$m_s = 3$

$m_q = 2$

$m_t = -2$

Quindi solo le rette sono parallele

$r$

$q,$

perché sono gli unici ad avere pendenze uguali.

Esercizio 2

Trova l’equazione esplicita della retta parallela alla retta

$r$

e cosa succede oltre questo punto

$P(0,2).$

essere sincero

$r:$

$r: \; y=3x-1$

vedi soluzione

In modo che la linea sia parallela alla linea

$r,$

entrambi devono avere la stessa pendenza. e la pendenza della linea

$r$

è 3:

$m = 3$

Pertanto, l’equazione esplicita della retta da trovare sarà:

$y=3x+n$

E una volta conosciuta la pendenza della retta, possiamo calcolare l’intercetta sostituendo il punto che appartiene alla retta nell’equazione della retta:

$P(0,2)$

$y= 3x+n \ \xrightarrow{x=0 \ ; \ y=2} \ 2=3\cdot 0 +n$

$2=0+ n$

$2= n$

Quindi l’equazione esplicita della retta è:

$\bm{y=3x+2}$

Esercizio 3

Calcolare il valore delle incognite

$a$

$b$

in modo che le due rette seguenti siano parallele:

$r: \ 2x-4y+6=0 \qquad \qquad s: \ x+ay+b=0$

vedi soluzione

Le linee sono descritte in forma di equazione generale (o implicita). Pertanto, affinché le due rette siano parallele, i loro coefficienti A e B devono essere proporzionali, ovvero deve essere soddisfatta la seguente equazione:

$\cfrac{2}{1} = \cfrac{-4}{a}$